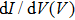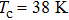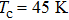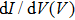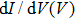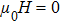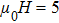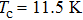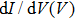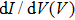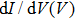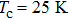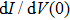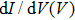† Corresponding author. E-mail:
In this work, we discuss the origin of several anomalies present in the point-contact Andreev reflection spectra of (Li1−xFex)OHFeSe, LiTi2O4, and La2−xCexCuO4. While these features are similar to those stemming from intrinsic superconducting properties, such as Andreev reflection, electron-boson coupling, multigap superconductivity, d-wave and p-wave pairing symmetry, they cannot be accounted for by the modified Blonder–Tinkham–Klapwijk (BTK) model, but require to consider critical current effects arising from the junction geometry. Our results point to the importance of tracking the evolution of the dips and peaks in the differential conductance as a function of the bias voltage, in order to correctly deduce the properties of the superconducting state.
Point-contact spectroscopy (PCS) has proved to be a simple yet powerful tool for investigating the properties of metallic and superconducting materials.[1] This technique relies on the formation of a point-contact between two metals, or a metal and a superconductor, allowing for a current I to flow through the resulting junction when a bias voltage V is applied. Typical experiments consist in measuring differential conductance 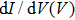
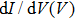
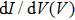
In comparison to conventional superconductors, unconventional superconductors host a rich diversity of phenomena, including pseudogap,[4] d-wave/p-wave pairing symmetry[5,6] or multi-band superconductivity,[7,8] that influence the PCAR spectra. For instance, if tunneling occurs along the nodal direction, a zero bias conductance peak (ZBCP) is detected around V = 0. This effect, arising from the Andreev reflection between positive and negative phase in a k-dependent nodal gap,[9] was evidenced in La2−xCexCuO4 and YBa2Cu3O7−δ.[10,11] Another example is the appearance of dips and ZBCP in the differential conductance spectra, indicating the existence of p-wave superconductivity.[12,13] This is due to the existence of non-trivial topological edge modes. The existence of multiple energy gaps arising from multi-band superconductivity also leaves a clear imprint in the spectra, when the coupling between the gaps is weak. This was namely observed in MgB2[14,15] and in iron-based superconductors (FeSe,[16] (Li1−xFex)OHFeSe,[17] LaFeAsO0.9F0.1,[18,19]) as evidenced by the observation of multiple coherence peaks.
Although the anomalies observed in the PCAR spectra might originate from the intrinsic properties of the unconventional superconductors under study, other less exciting phenomena related to the configuration of the junction between the tip and the sample surface should be seriously considered. Indeed, similar anomalies were widely observed both in conventional and unconventional superconductors and were attributed to diverse causes such as the superconducting proximity effect, the formation of an intergrain Josephson junction at the tip apex or heating in the point-contact, leading to a local decrease in the critical current of the superconductor.[20,21] Therefore, caution has to be exerted when interpreting the experimental data. In particular, phenomena inducing intrinsic properties of the sample and those related to the geometry might give similar features in the spectra. This could lead to erroneous conclusions on the nature of superconductivity in unconventional superconductors if the Blonder–Tinkham–Klapwijk (BTK) model,[22,23] usually employed to describe the spectra, is not amended to account for the additional effects.
In this work, we aim at clarifying the interpretation of experimental PCAR spectra, by making a clear distinction between anomalies arising from the intrinsic properties of unconventional superconductors and those coming from the junction geometry. In particular, we address the situation where the reduction of the superconducting critical current plays a crucial role in the interpretation of the data. This is the case (i) when heating occurs in the point-contact and (ii) when the tip is in series with an intergrain Josephson junction. After that we briefly review the proximity effects which will introduce similar anomalies. Under these circumstances, the results from the BTK model need to be complemented by additional contributions to account for the features in the spectra. With this in hand, we are ready to confront the theoretical description to some experimental examples of PCAR on unconventional superconductors, where it is of paramount importance to go beyond the BTK model to properly understand the superconducting properties of the sample. The experiments shed light on possible misinterpretation of the spectra, arising from the confusion between critical current effects and i) Andreev reflection, ii) multiband superconductivity, iii) p-wave superconductivity, and iv) d-wave superconductivity.
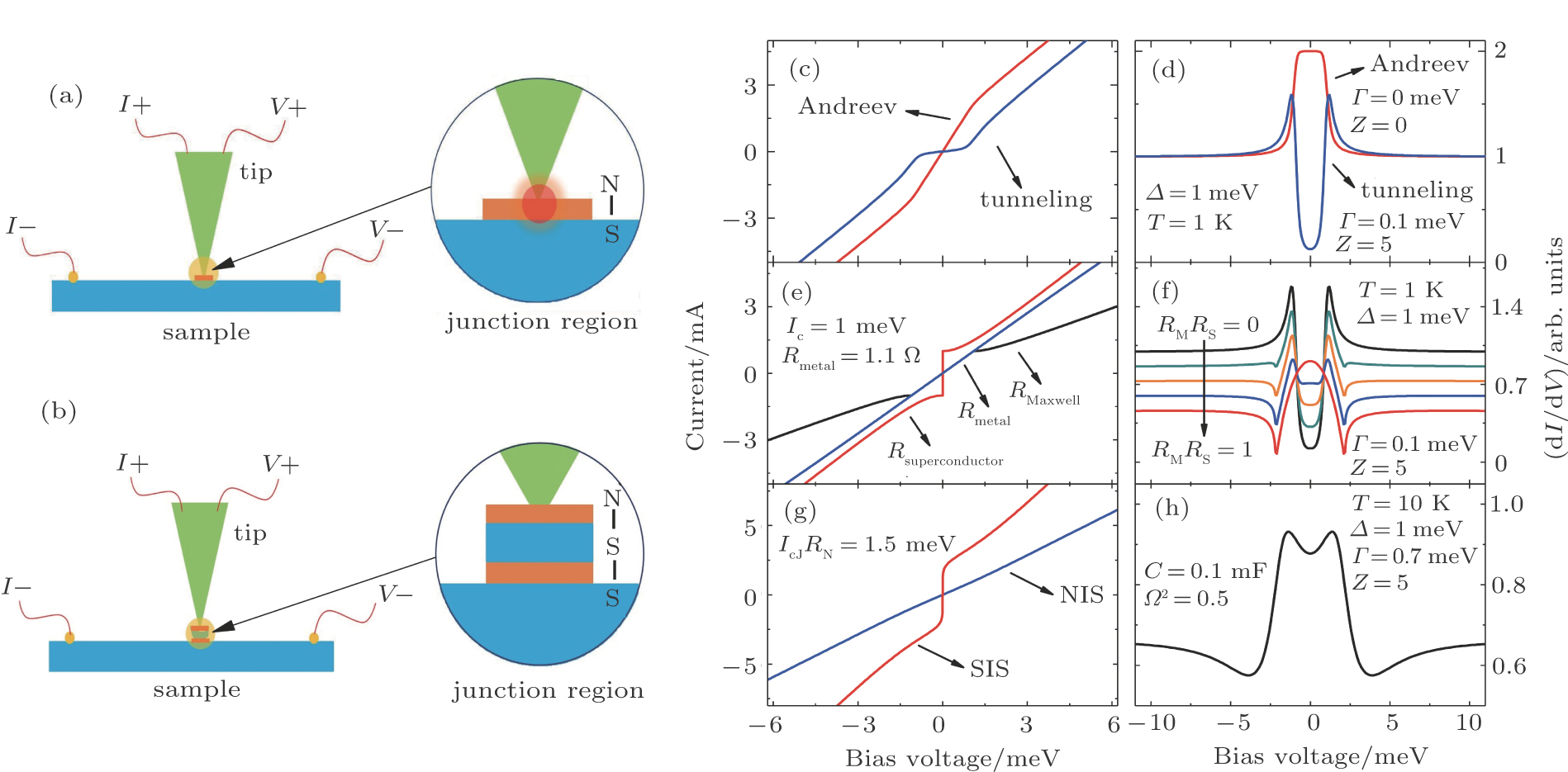
An ideal point-contact junction essentially consists in a metal in the non-superconducting state (N) brought in contact with a superconductor (S), separated by a thin insulating barrier (I). A simplified model, the so-called BTK model,[23] has been introduced by Blonder, Tinkham, and Klapwijk to describe PCAR in such N/I/S junctions. Assuming a unidimensional junction at zero temperature, aligned with the x axis, the repulsive insulating barrier at the interface is represented by the potential energy 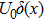
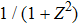
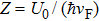
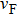
Under these assumptions, the current INIS across the junction can be calculated analytically, by considering the probability of occurrence of different processes that an electron coming from the N side may undergo at the interface. In the BTK model, these include Andreev reflection (with a probability A), ordinary specular reflection (B), and transmission as an electron-like (C) or hole-like (D) quasiparticle. As a result, the current INIS can be written as
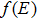
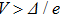
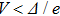
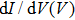
As a final remark, note that the BTK model is valid only under the assumption that heating and proximity effects are negligible in the point-contact region. In practice, satisfying these conditions implies that the characteristic size a of the contact should be smaller than the electron mean free path l and the coherence length ξ, respectively.[8]
Up to now, we considered point-contacts with a small characteristic radius 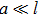
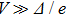


On the contrary, in the thermal regime where 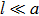
In general, in the situation depicted in Fig.

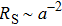

The features of RS have been described previously by the BTK model. The I(V) characteristics of RM can be plotted using Eq. (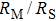
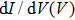
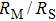
In polycrystalline superconductors, where the intergrain weak-coupling effect plays an important role, the BTK model does no longer provide a satisfying description of the junction. Indeed, in this situation, the junction between the tip and the sample surface can in general be represented by the point-contact (N/I/S) described previously, associated in series with a Josephson junction (S/I/S), accounting for the connection between the tip and the superconducting grains. This situation is depicted in Fig.
The total voltage V across the junction is then the sum of two contributions: the point-contact voltage VNIS, described by the BTK model, and the Josephson junction voltage VSIS. In the presence of thermal noise and with the assumption that the associated capacitance C is small, the contribution of VSIS can be calculated by the resistively shunted junction (RSJ) model,[20,28] and is written as
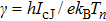
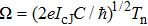
The I(V) curve corresponding to the typical response of a Josephson junction is shown in red in Fig. 
The features of the spectra resulting from the association of the NIS junction and SIS junction depend strongly on their normal-state resistances RNIS and RSIS, respectively. We can calculate the I(V) characteristic and the differential conductance by using the following relations: 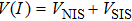

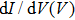
In some point-contacts, the tip is not sharp enough, and Andreev reflection effect becomes weaker than a fine junction. In this case, SIS junction dominates the spectrum, and a ZBCP can be observed, which is higher than 2[20,29] (the maximum value expected from the conventional Andreev reflection). It is known that ZBCP is not expected for an ideal RSJ model except for a point of divergence at zero point. However, when a small normal RNIS connect in series with RSIS, at 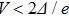
Finally, if the insulating layer in the SIS is substituted by a normal metal, i.e., SNS, multiple Andreev reflection may happen at the interface between the superconductor and the metal, which can also induce an enhanced ZBCP higher than 2.
Proximity effects occurring at the interface between a metal and a superconductor might give rise to additional features in the conductance spectra.[30] Indeed, due to the diffusion of Cooper pairs from the superconductor to the metal, a weak superconducting layer is formed at the superconductor/metal interface, with a superconducting gap smaller than the bulk value. Therefore, Andreev reflection in the proximity effect layer occurs for voltages lower than the bulk value. However, the bias voltage still needs to be large enough to overcome the bulk gap, so a dip in the conductance spectrum appears between those values. The proximity effect can be accounted for by introducing two gap values in the model, giving rise to sharp dips between the voltages corresponding to the gap energies. This effect is more prominent in the case of a clean contact with a low Z.
The point-contact junctions between the samples and the probe are established using home-made Pt/Ir tips or a small drop of Ag paste. The assembly is installed in a Quantum Design PPMS system to achieve temperatures as low as 1.8 K, and high magnetic fields, up to 15 T. Sample stage motion is allowed on the x-axis and z-axis, in the range of 3 mm and 2.5 mm respectively. The differential conductance 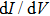
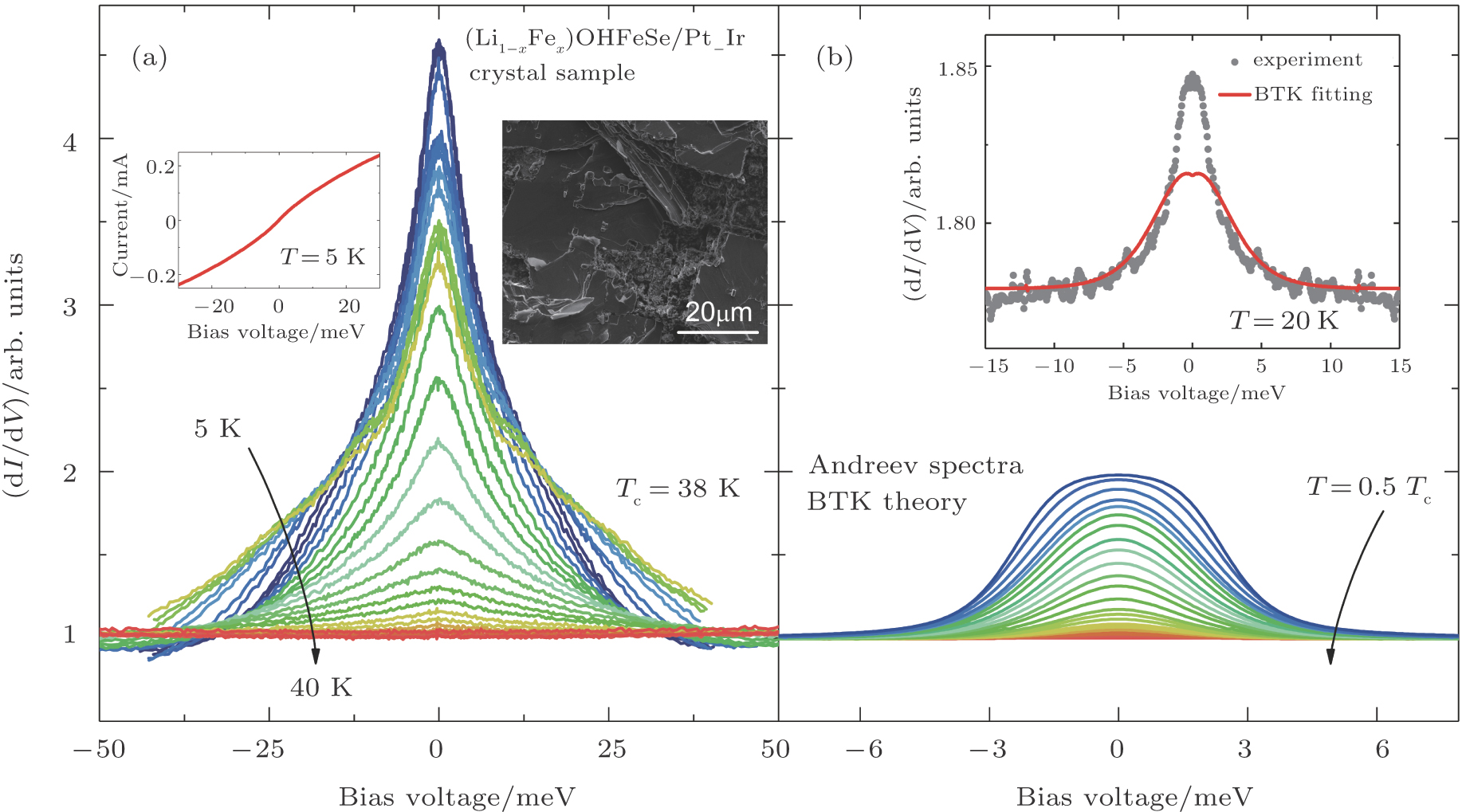
The experimental PCAR spectra obtained on a point-contact between an (Li1−xFex)OHFeSe sample and a PtIr tip are shown in Fig. 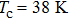
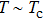

The differences between the experimental spectra and the BTK model can be attributed to critical current effects, arising from the formation of an S/I/S(S/N/S) junction at the apex of the tip or the thermal effect. Indeed, as explained previously, the response of such a junction might lead to a large peak at zero bias, with amplitude significantly larger than 2. In view of the picture taken by scanning electron microscope showing easily broken surface [See the inset in Fig.
These spectra are usually observed in iron-based superconductors,[3] such as the sample we studied here, as their surface is often fragile. As a consequence, in the process of forming a point-contact between the tip and the sample, the surface frequently suffers degradation. The resulting debris or defects lead to the formation of an S/I/S(S/N/S) junction between the tip apex and the sample. Another possible explanation for the formation of these junctions involves the bad crystallinity of some samples, such as polycrystalline systems, where the intergrain coupling plays a significant role. A more compelling evidence would require nanoscopic imagin of the tip-sample interface which is not straighforward even with the technology available today.
Various unconventional superconductors were found to exhibit a multiband behavior.[14,35–37] For instance, in iron-based superconductors, Angle-Resolved Photoemission Spectroscopy (ARPES) measurements widely show a signature of multiband superconductivity, with a hole pocket in the Γ points and an electron pocket in the M point.[36,38] In these systems, PCAR spectroscopy is a tool of choice to extract information on the band coupling. In many compounds, such as FeSe[16] and (Li1−xFex)OHFeSe,[17] the spectra point to the existence of two superconducting gaps. However, caution has to be exerted when interpreting 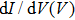
Figure 
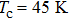
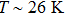
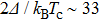
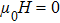
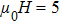
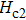
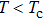
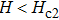

For p-wave superconductors, PCAR spectra show double dips and ZBCP, resulting from the existence of non-trivial edge modes in unconventional topological superconductors.[13] These features have been observed in CuxBi2Se3,[12] Cd3As2,[40] and TaAs.[41] We performed PCAR measurements on a LiTi2O4 film (
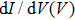
However, the experimental features cannot be attributed to p-wave superconductivity, since LiTi2O4 is a normal metal without topological features in band structure.[42,43] This is also backed up by other experimental techniques, such as point contact measurements[44] and specific heat measurements,[45] that clearly point to the existence of s-wave superconductivity. The observed features can however be explained by critical current effects. This is further supported by the fact that in both samples sets, increasing T or H leads to the disappearance of the small irregularities in the spectra, attributed to weak-links between superconducting grains. As for the split peaks observed in spectra, it can be generated by several mechanisms: proximity effect, two superconducting gaps, and weak-links between superconducting grains. The case of two superconducting gaps can be ruled out through the analysis above. We firstly try to fit this anomaly by proximity effect. However, the fitting result is not ideal even trying much different values of fitting parameters. On the contrary, the features like double dips and two split peaks can be well fitted by the model of an N/I/S junction in series with two S/I/S junctions at the same time, as shown in Fig.
Strong electron–boson coupling might also be invoked to explain the humps/dips features in the tunneling spectra,[46–48] by establishing a correspondence with the electron–boson spectra function 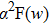
In cuprate superconductors, the 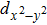
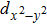
A characteristic feature of superconductors with d-wave symmetry is the ZBCP observed in the PCAR spectra, stemming from Andreev reflection occurring between positive and negative phases in a k-dependent node gap.[9,51] However, the particular shape of the spectra is strongly dependent on α, and dips and peaks might appear as the angle is changed. In contrast to the Andreev reflection spectra for an s-wave superconductor, the zero bias conductance might be larger than 2, thus making it difficult to distinguish from critical current effects. Figure 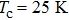
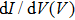

The ZBCP observed in LCCO can be satisfyingly explained by invoking critical current effects. The sharp increase of the 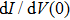
Point-contact spectroscopy in the Andreev reflection regime constitutes a tool of choice to study unconventional superconductors. Indeed, some of the features observed in the differential conductance 
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] |