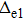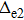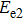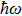† Corresponding author. E-mail:
We study the ground state energy of an atom interacting with an oscillating optical field with electric dipole and quadrupole coupling. Under the rotating wave approximation, we derive the effective atomic Hamiltonians of the dipole/quadrupole coupling term within the perturbation theory up to the second order. Based on the effective Hamiltonians, we analyze the atomic ground-state energy corrections of these two processes in detail. As an application, we find that for alkali-like atoms, the energy correction from the quadrupole coupling is negligible small in comparison with that from the dipole coupling, which justifies the so-called dipole approximation used in literatures. Some special cases where the quadrupole interaction may have considerable energy corrections are also discussed. Our results would be beneficial for the study of atom–light interaction beyond dipole approximation.
The research on the interactions between electromagnetic field and matter plays a centre role in the progress of contemporary physics. A fundamental startpoint is to consider the coupling between atom and light, which is responsible for many physical phenomena. For example, the light emission and absorption of atoms and molecules are powerful sources to detect the underlying atomic structures and dynamic processes. It also enables us to manipulate the atomic internal and external degrees of freedom with the atom–light coupling, to realize states near or far from the thermodynamic equilibrium.[1–4]
The physics of ultracold atoms focuses on coherent quantum motion of atoms in the ultra-low temperature and many-body effects in these quantum gases due to the interaction between atoms.[5–8] Interaction between atoms and laser lights plays an important role in controlling cold atom systems, ranging from matured technologies such as laser cooling, optical trapping, and optical lattices to the latest developments such as synthetic gauge field and stimulated Raman adiabatic passage to achieve the ground state polar molecules.[9–13] In most of the studies in cold atom physics, the atom–light interaction is treated in the frame of dipole approximation which refers to the interaction between atomic electric dipole and the laser light, while the electric quadrupole interaction effect is usually neglected. It was shown that the rarely considered atomic electric quadrupole may lead to fractional frequency shifts in an optical lattice clock.[14–17] Nevertheless, the corrections there are estimated in the harmonic oscillator approximation and the general result brought by the electric quadrupole interaction is not clear. Especially, in what circumstances the electric quadrupole interaction may play a critical role and cannot be neglected is a question. In this paper to address this problem, we go beyond the harmonic approximation and take into account the dipole and quadrupole interactions on an equal foot.
The rest of this paper is organized as follows. In Section
It is well known from a textbook of classical electrodynamics that, if a localized charge distribution described by 

 |
If the potential Φ is slowly varying over the region where 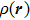
 |
Utilizing the definition of the electric field 

 |
Substituting 
 |

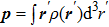
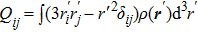
In general, due to the total charge of an atom is zero, the dipole term becomes the most important one in the atom–light interaction. In this paper, without loss of generality, we take an oscillatory light field 
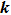


 |
 |
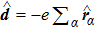
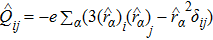
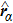
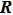
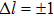
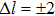
The atom is described by the Hamiltonian
 |


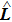
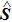

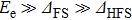
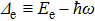

In the frame rotating with frequency ω via a unitary transformation 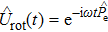
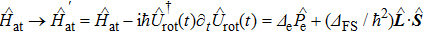
 |
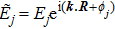
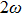

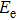
 |
Dipole interaction is thoroughly discussed in Ref. [19]. In the regime of 

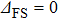
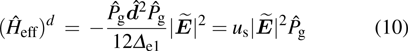 |
 |
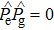

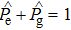
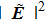
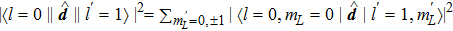
When the effect of the fine-structure splitting is considered, the dipole interaction yields a vector light shift in addition to the scalar light shift of Eq. (
 |
 |
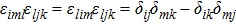
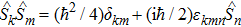

Let us now turn to the quadrupole transition (see the blue arrow in Fig.
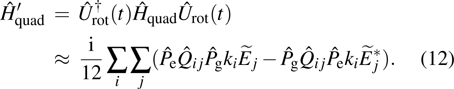 |
When we first consider no fine structure case with 
 |

Let us then consider a finite fine-structure coupling. Using the relation 
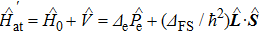
 |
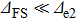
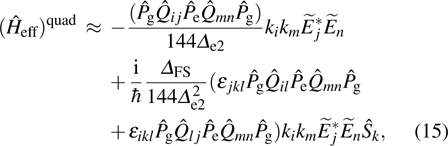 |
We now turn to investigate the effect of the dipole and quadrupole interaction on the ground state energy. It is shown that in Eqs. (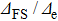
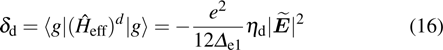 |
 |
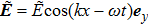
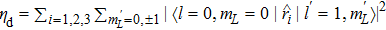

The energy corrections are then characterized by the ratio between two transitions, which is
 |

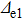
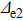
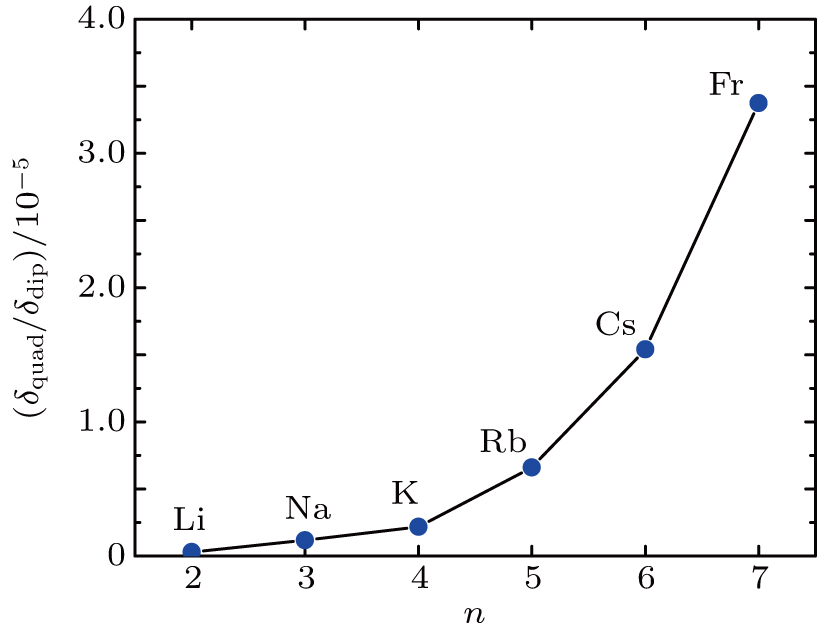
Now we do numerical comparisons for alkali atoms as examples to get a more intuitive understanding. It is reasonable to use hydrogen atom wave functions 



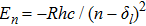


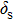




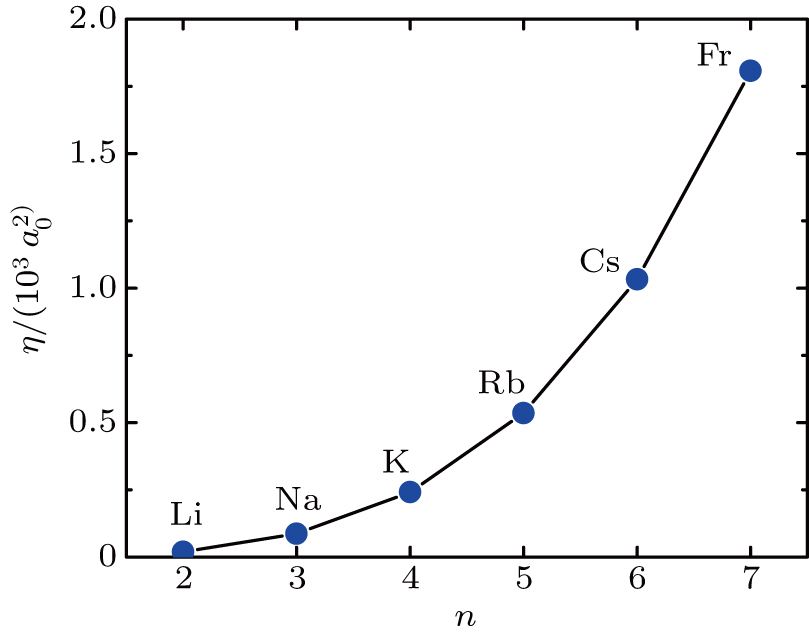 | Fig. 2. (color online) The transition matrix element ration η in terms of principle quantum number n. η is in unit of 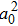
|
| Table 1.
Electric dipole and quadrupole impacts on the alkali atomic ground state manifold. . |
Figure 








Despite of the validity of the dipole approximation for alkali atoms, there may exist the situations where the quadrupole effect is considerable and one needs to go beyond the dipole approximation. First, we notice that, we have used a plane wave light field in above discussions, which naturally falls into the electric dipole approximation regime with 
In this paper, we have studied the dipole and quadrupole coupling between an atom and a light field. In the far off-resonance case, we derive the effective Hamiltonians to describe the effects on the ground state manifold brought by the dipole and quadrupole transitions. We find that, for the alkali-like atoms, the energy correction from dipole transition is dominant and the dipole approximation can be applied. While for other cases like the Rydberg atom with a very large size, the molecular with large quadrupole moment, the correction induced by the quadrupole interaction may become considerable and one needs to go beyond the dipole approximation. Future studies would include Rydberg atoms, a gaussian-like light field, a many-electron atom, and so on.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] |