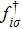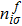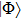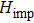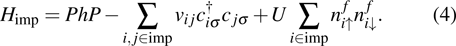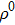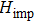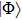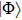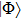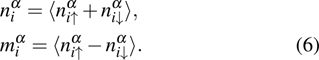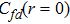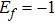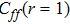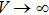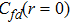Phase diagram, correlations, and quantum critical point in the periodic Anderson model
1. IntroductionHeavy fermion materials[1] display abnormal behaviors in many respects, such as large magnetic susceptibility and specific-heat coefficient,[2] unconventional superconductivity,[3–6] and non-Fermi liquid behavior.[7] Most of the heavy fermion compounds contain rare earth elements with partially filled f shells. The unusual properties of the heavy fermion compounds are usually attributed to the admixture of the local f orbital with the conduction band. Kondo lattice model (KLM) and periodic Anderson model (PAM)[8] are believed to capture the physics of the heavy fermion materials. KLM can be derived from PAM by fixing the filling of the f orbital to 1 at the large U limit. PAM is an asymmetric two-band model, which contains conduction c orbital and correlated f orbital. Although simple, it displays rich physics, such as the valence fluctuation,[9] the appearance of Lifshitz transition,[10–12] and the competition between the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction and the Kondo interaction.[13–15]
Among the above phenomena, the Lifshitz transition is of particular interest. A transition associated with the change of Fermi surface topology is the so-called Lifshitz transition.[16] There have been several experiments exhibiting the Lifshitz transition in heavy fermion materials. The Hall coefficient of YbRh2Si2 shows a rapid change as a function of the magnetic field,[17] and this can be interpreted by the collapse of the large Fermi surface. Measurement of De Haas–van Alphen effect on CeRh1−xCoxIn5 shows a Fermi surface reconstruction as a function of x.[18] A Fermi surface reconstruction is also observed in the antiferromagnetic phase of CeRhI5 under a magnetic field.[19] Recent angle-resolved photoemission spectroscopy measurement on YbAl3 discovers that the Lifshitz transition could be caused by the valence fluctuation.[20]
Meanwhile there are many theoretical studies about the Lifshitz transitions on models, including studies on Kondo lattice model[21–23] and periodic Anderson model.[10–12] The mean field theory is widely used in the above studies. It could be applied to any parameters, but it is not a many-body method. By introducing Gutzwiller projection, variational Monte Carlo simulation has many-body nature, but it quite relies on the trial wavefunctions. Dynamical mean field theory (DMFT) avoids these problems, but it makes a simplified treatment of the interactions. In this work, we use the density matrix embedding theory (DMET) to study the ground state properties of the two-dimensional PAM. DMET is a quantum cluster method the same as DMFT, but it does not have bath discretization error and can be practically computed without analytic continuation.
This paper is organized as follows. In Section 2, we briefly describe the model and provide details of the method. Our main results on the phase diagrams, physical quantities and discussion are included in Section 3. Finally, a summary is provided in Section 4.
2. Model and methodWe study the periodic Anderson model on a two-dimensional square lattice. The Hamiltonian reads
where


and
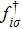

are the creation (annihilation) operators for the conduction and localized orbitals on site
i with spin
σ, respectively,
t is the hopping integral between the neighboring conduction orbitals,
Ef is the on-site energy of the localized orbital (
f state), which defines the relative position of the
f state with respect to the Fermi energy of the conduction orbital (
c state),
V is the hybridization strength between the
c and
f states on the same site, and
U is the on-site Coulomb repulsion of the
f states.
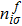
is the number of f electrons on site
i with spin
σ.
Density matrix embedding theory was first proposed in 2012,[24] since then it has been applied to several different systems, including the Hubbard model,[25–28] the interacting electron–phonon model,[29] and the ab-initio quantum chemistry problem.[30–32] By introducing an auxiliary noninteracting system, DMET maps the original lattice model to an interacting quantum impurity model, then solves the impurity model exactly. The impurity model and the auxiliary system are linked by a self-consistency condition of the one-particle-reduced-density-matrix (1-PDM). By construction, the number of bath orbitals in DMET is finite, thus there is no bath discretization error and the computational cost is much lower.
Like the other quantum cluster methods, DMET first divides the lattice sites into different clusters, which tile the whole lattice. In order to keep the translational invariance, we always choose clusters to be unit cells of the lattice. Then the auxiliary Hamiltonian h is
where
h0 is the one body term of
H, and
v is the correlation potential within the cluster. In this work, we do not consider the superconducting phase, so
v has the form
Here
C is the cluster that we partition the lattice into. Since the correlation potential is only within the cluster, it is block diagonal. It can be considered as an approximation of the local interaction.
From the ground state
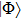 of h, the embedding basis could be constructed. We choose the sites in one of the clusters as the impurity sites, and the sites from the rest of the clusters as the environment sites. There are several mathematically equivalent unitary transformations (we do not get into the details here, for more details, please read Ref. [27]). By applying the transformation, all the orbitals from the environment sites linearly combine into bath orbitals, core orbitals, and virtual orbitals. The core (virtual) orbitals are completely empty (full), thus only the bath orbitals are entangled with the impurity orbitals. By applying the projection operator P which projects the Hamiltonian h into the space spanned by the impurity orbitals and bath orbitals, removing the correlation potential on the impurity orbitals, and bringing back interactions on the impurity orbitals, we can obtain the impurity Hamiltonian
of h, the embedding basis could be constructed. We choose the sites in one of the clusters as the impurity sites, and the sites from the rest of the clusters as the environment sites. There are several mathematically equivalent unitary transformations (we do not get into the details here, for more details, please read Ref. [27]). By applying the transformation, all the orbitals from the environment sites linearly combine into bath orbitals, core orbitals, and virtual orbitals. The core (virtual) orbitals are completely empty (full), thus only the bath orbitals are entangled with the impurity orbitals. By applying the projection operator P which projects the Hamiltonian h into the space spanned by the impurity orbitals and bath orbitals, removing the correlation potential on the impurity orbitals, and bringing back interactions on the impurity orbitals, we can obtain the impurity Hamiltonian
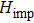
Only the bath orbitals and impurity orbitals constitute the impurity model

. Because the bath orbitals are at most as many as the impurity orbitals, the impurity model can be solved exactly. In this work, we use the density matrix renormalization group (DMRG) method
[33] to solve the impurity model
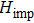
.
As we mentioned previously, with the 1-PDM
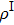 of
of
 , the correlation potential is determined by a self-consistent procedure. Our goal is to minimize the difference of
, the correlation potential is determined by a self-consistent procedure. Our goal is to minimize the difference of
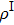 and 1-PDM
and 1-PDM
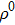 which is derived by downfolding
which is derived by downfolding
 to the impurity and bath space
to the impurity and bath space
When optimizing
f(
v), the ground state of
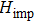
is fixed, the optimal
v is used to update
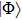
, so does

. Then the impurity Hamiltonian

as well as

are updated too. Thus the self-consistent loop is formed.
In summary, the DMET calculation include the following steps. (i) Choose an initial guess of the correlation potential v0. (ii) Solve the auxiliary lattice Hamiltonian to obtain the lattice wave function
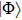 . (iii) The embedding basis is constructed from the lattice wave function
. (iii) The embedding basis is constructed from the lattice wave function
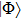 . (iv) Transform to the embedding basis, and add the interaction to obtain the impurity model. (v) Use the DMRG impurity solver to compute the ground state of the impurity model, and calculate the corresponding one particle reduced density matrix. (vi) Update the correlation potential v to minimize the difference of the one particle reduced density matrix between the auxiliary Hamiltonian h and the impurity Hamiltonian
. (iv) Transform to the embedding basis, and add the interaction to obtain the impurity model. (v) Use the DMRG impurity solver to compute the ground state of the impurity model, and calculate the corresponding one particle reduced density matrix. (vi) Update the correlation potential v to minimize the difference of the one particle reduced density matrix between the auxiliary Hamiltonian h and the impurity Hamiltonian
 . (vii) Go back to step (ii) until the correlation potential v converges.
. (vii) Go back to step (ii) until the correlation potential v converges.
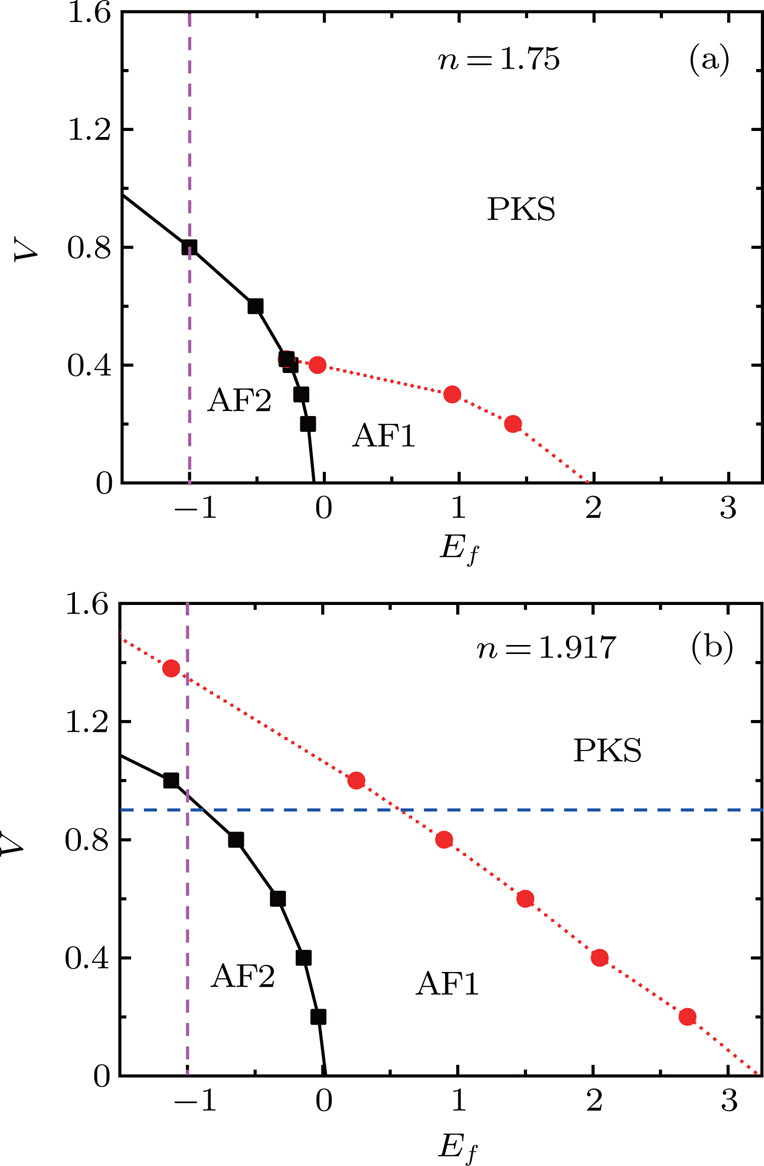
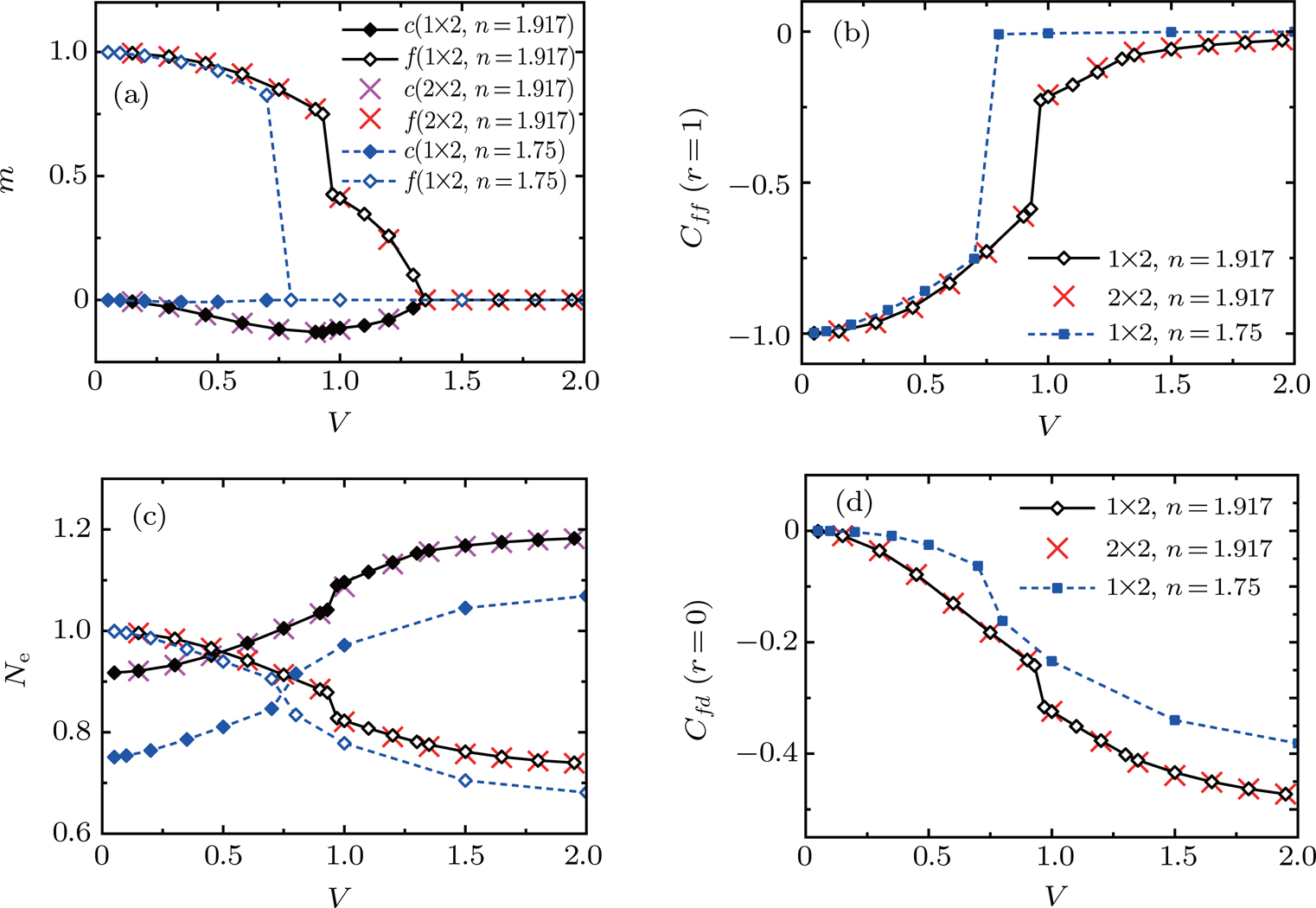
3. ResultsWe have run the DMET calculation of PAM on a two-dimensional square lattice. The lattice size of our calculation is 72 × 72, and the cluster we used is 1 × 2 or 2 × 2. From figs. 2 and 3, we can see that the calculations with the 1 × 2 and 2 × 2 clusters produce almost the same results. There is not so much finite cluster error in this work. The following results are all done by fixing the on-site Coulomb repulsion U to 8.0 (hopping integral t = 1), since there have been many discussions on the U–V phase diagram.
We show the ground state V–Ef phase diagrams in Fig. 1. As Ef increases, there are three different phases: antiferromagnetic phase 2 (AF2), antiferromagnetic phase 1 (AF1), and paramagnetic Kondo singlet phase (PKS). The local moment is nonzero in both AF1 and AF2 phases, while it is zero in the PKS phase. There is a Fermi surface reconstruction between the AF1 and AF2 phases, which leads to a first-order phase transition between the two antiferromagnetic phases. At filling n=1.75, the AF1 phase only appears at small value of V, while at filling n=1.917, the AF2 phase shrinks, and the AF1 phase amplifies. When Ef is fixed to −1 at filling n=1.75, one could go through the AF2 phase directly to the PKS phase. At filling n=1.917, if one fixes
 , the AF1 phase is between the AF2 phase and PKS phase.
, the AF1 phase is between the AF2 phase and PKS phase.
Now we discuss how the physical quantities change in different phases. The number of electrons and the local moment are defined as
Here
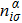
is the number of spin
σ electrons of
α orbital on site
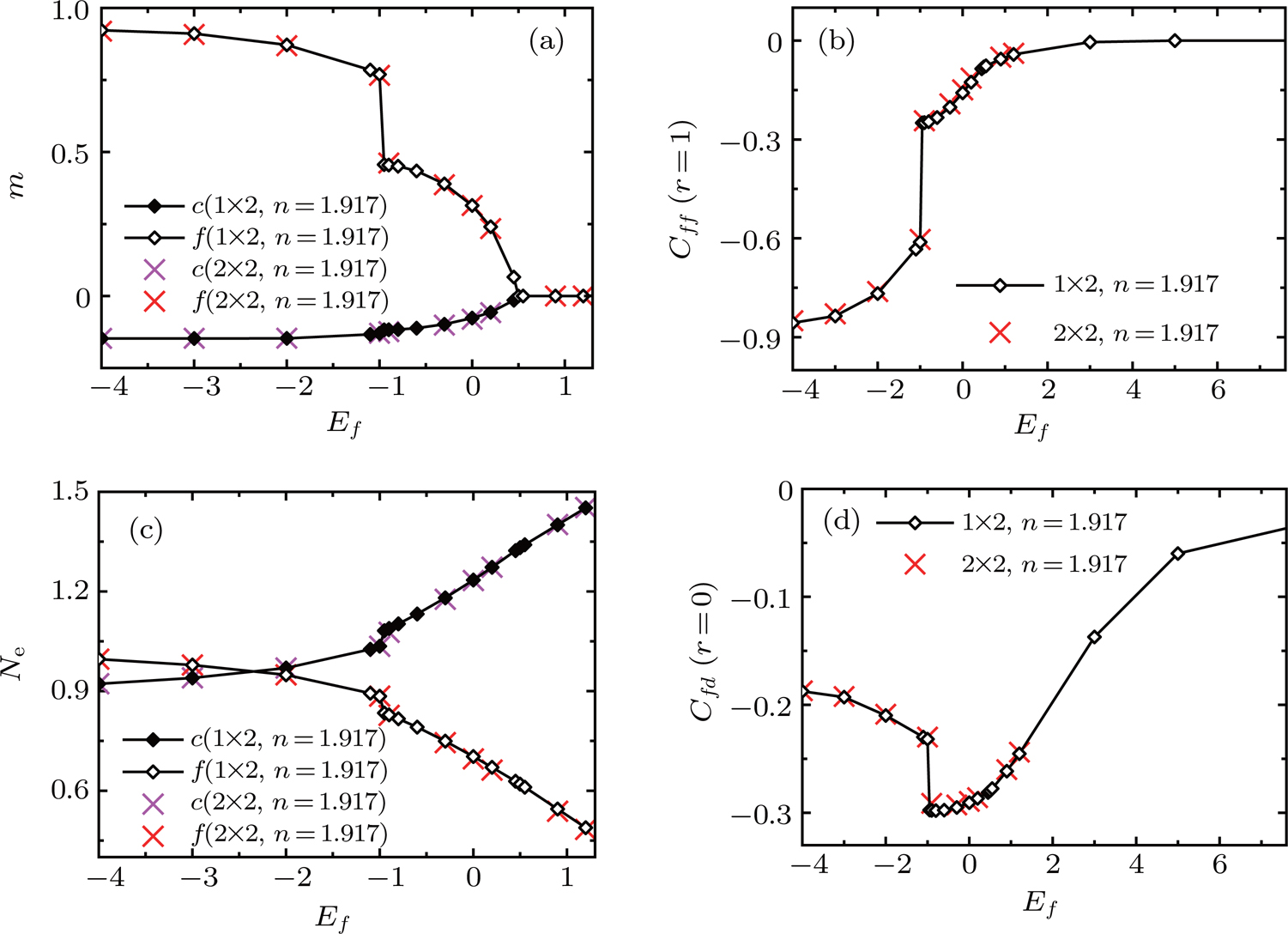
i. First we go through the horizontal dashed line (blue line) in Fig.
1(b) by fixing the hybridization
V to 0.9 at filling
n=1.917. The results are displayed in Fig.
2. The local magnetic moment and the number of electrons are shown in figs.
2(a) and
2(c).

is the symmetric case where the Fermi energy of the conduction orbitals is in the middle of the two
f orbital energy levels. The number of
f states (
nf) and
c states (
nc) are both 1.0 at the half filling symmetric case. Away from half filling,
nf is close to 1.0, while
nc is slightly smaller than 1.0. As
Ef increases, the electrons are more and more likely to occupy the
c states, so
nc increases while
nf decreases. The value of
V is small here, so the RKKY effect dominates, there is an antiferromagnet long range order in both the
f orbitals and the
c orbitals. The localized
f orbitals have larger local moments, while the conduction
c orbitals have smaller local moments. There is antiferromagnetic coupling between the
f and
c orbitals on the same site, thus
mf and
mc always have the opposite signs. The local moments decrease as
Ef increases and become zero in the paramagnetic phase. Before the magnetic transition occurs, both local moment and number of electrons have a discontinuity. It is due to the Fermi surface reconstruction which causes a first order phase transition. This is the so-called Lifshitz transition.
In order to understand the magnetic properties, we also calculate the spin–spin correlation functions. The correlation functions are defined as
The results of the spin–spin correlation functions are shown in figs.
2(b) and
2(d). Figure
2(b) is the correlation function between neighboring
f states

. In the AF2 and AF1 phases, it has a non-zero value. There is a discontinuity at the transition point between the two phases as another evidence of the Lifshitz transition. As the antiferromagnetic long range order disappears in the PKS phase,
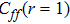
soon becomes zero.
Figure 2(d) is the correlation function between the f and c orbitals on the same site. The negative value of the correlation function suggests the antiferromagnetic coupling between the f orbital and c orbital. As shown in Fig. 2(d), the absolute value of correlation increases in the AF2 phase as Ef increases. We have shown that the local moments of both f orbitals and c orbitals are decreasing. The increasing on the correlation magnitude indicates the formation of Kondo singlet even in the antiferromagnetic phase. It reaches maximum at the Lifshitz transition point, and in the AF1 phase it decreases. In the PKS phase, the correlation approaches zero as Ef increases. Due to the formation of Kondo singlet between the f orbitals and c orbitals, the correlation has a non-zero value. However in the
 limit, all the electrons occupy the c orbitals, so
limit, all the electrons occupy the c orbitals, so
 is approaching zero.
is approaching zero.
It is interesting to examine
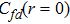 in the AF1 phase. We mentioned that the Kondo singlet state is formed even in the AF2 phase, this should occur in the AF1 phase too. The correlation function decreases slowly in this phase. The reason is that the contribution from antiferromagnetic becomes weak, and at the same time the number of f electrons decreases rapidly, the number of Kondo singlet pairs also decreases. In the PKS phase, the number of f electrons decreases further, so the correlation function decreases fast.
in the AF1 phase. We mentioned that the Kondo singlet state is formed even in the AF2 phase, this should occur in the AF1 phase too. The correlation function decreases slowly in this phase. The reason is that the contribution from antiferromagnetic becomes weak, and at the same time the number of f electrons decreases rapidly, the number of Kondo singlet pairs also decreases. In the PKS phase, the number of f electrons decreases further, so the correlation function decreases fast.
Next we fix the on-site energy of the f orbital
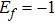 at filling n=1.75 and n=1.917 (along the vertical dashed line in figs. 1(a) and 1(b)), the results are displayed in Fig. 33. Since the Kondo coupling
at filling n=1.75 and n=1.917 (along the vertical dashed line in figs. 1(a) and 1(b)), the results are displayed in Fig. 33. Since the Kondo coupling
 , at small (large) V, the Kondo coupling is weak (strong). When the Kondo coupling is weak, the RKKY coupling dominates, and the antiferromagnetic long range order appears. As V increases, the Kondo coupling dominates, and the AF order is destroyed. Now we discuss the results at different fillings in detail.
, at small (large) V, the Kondo coupling is weak (strong). When the Kondo coupling is weak, the RKKY coupling dominates, and the antiferromagnetic long range order appears. As V increases, the Kondo coupling dominates, and the AF order is destroyed. Now we discuss the results at different fillings in detail.
At filling n=1.917, the competition of RKKY coupling and Kondo coupling leads to the AF1 phase. At small V, the RKKY coupling dominates, and the AF2 order is formed. As V increases to the intermediate region, the AF1 phase appears, and at large V, the Kondo singlet is formed between the f orbitals and c orbitals. The local moment is shown in Fig. 3(a), the mf–V curve is quite similar to the mf–Ef curve. However the local moment of the c orbitals, mc, is slightly different. In the AF2 phase, it increases as V increases, and reaches maximum at the Lifshitz transition point. The behavior of the correlation between two neighboring f orbitals is also similar to that in the
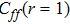 –Ef curve. The number of electrons is also varying as V changes, since the effect of V is to mix the two orbitals, and the on-site U makes the electrons be more likely to occupy the c orbitals. In the PKS phase, the numbers of electrons in different orbitals only change a little bit. The correlation between the f and c orbitals on the same site keep increasing as V increases. As
–Ef curve. The number of electrons is also varying as V changes, since the effect of V is to mix the two orbitals, and the on-site U makes the electrons be more likely to occupy the c orbitals. In the PKS phase, the numbers of electrons in different orbitals only change a little bit. The correlation between the f and c orbitals on the same site keep increasing as V increases. As
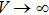 , it approaches −0.5.
, it approaches −0.5.
While at filling n=1.75, when
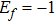 the AF1 phase does not exist. The transition between the AF2 phase and PKS phase is of first order, since the forms of Fermi surface are different in the two phases. There is a big step in both the f orbital local moment curve and the
the AF1 phase does not exist. The transition between the AF2 phase and PKS phase is of first order, since the forms of Fermi surface are different in the two phases. There is a big step in both the f orbital local moment curve and the
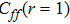 curve. The local moment of the c orbital is close to zero in the AF2 phase. The local magnetic moment of the f orbital and the correlation of the f orbitals are zero in the PKS phase. The behavior of the number of electrons is quite similar to that at filling n=1.917, except that the jump is not so obvious. Since the local moment of the c orbital is almost zero in the AF2 phase, the correlation of the on-site c and f orbitals is close to zero too. The magnitude of correlation increases slightly as V increases, in the PKS phase the magnitude of correlation increases rapidly.
curve. The local moment of the c orbital is close to zero in the AF2 phase. The local magnetic moment of the f orbital and the correlation of the f orbitals are zero in the PKS phase. The behavior of the number of electrons is quite similar to that at filling n=1.917, except that the jump is not so obvious. Since the local moment of the c orbital is almost zero in the AF2 phase, the correlation of the on-site c and f orbitals is close to zero too. The magnitude of correlation increases slightly as V increases, in the PKS phase the magnitude of correlation increases rapidly.
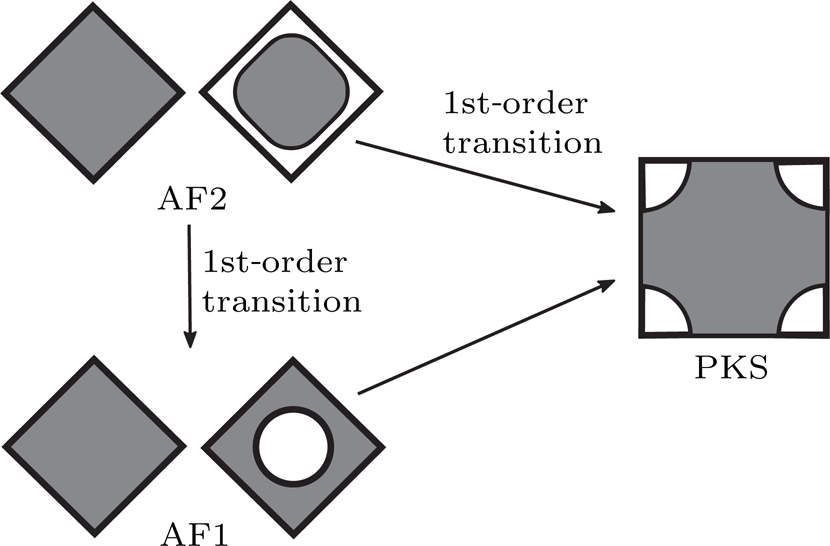
In the end, we discuss the Lifshitz transition. As we mentioned previously, the phase transition is caused by the Fermi surface reconstruction. By using the variational Monte Carlo method, Wanabe et al.[11] calculated the momentum distribution functions of different phases. They found that the f orbital does not contribute to the formation of Fermi surface in the AF2 phase. This indicates that the f orbital is completely localized in the AF2 phase. But it becomes itinerant in the AF1 phase as well the PKS phase. Other evidence of Fermi surface reconstruction is from the study of cellular dynamical mean field theory by De Leo et al.[34] They found that the AF2–AF1 transition is accompanied by a rearrangement of spectral weight. We find a discontinuity in both the magnetic moments and the number of electrons. In Fig. 4, the evolution of the magnetic moment versus Ef at different fillings is shown. At the transition point between the AF2 and AF1 phases, there are steps in both the mf curve and the mc curve. The latter is much smaller, which can hardly be seen in the figure. It is very clear that as it approaches half filling, the step of mf becomes smaller and smaller. The inset of Fig. 4 shows the magnitude of the step on mf. The step decreases as the filling increases, and becomes zero when the filling reaches half filling. At half filling, there is no difference between the AF2 and AF1 phases.
The Fermi surface topology in different phases is plotted in Fig. 5. The PKS phase is the ordinary Fermi liquid state with a large Fermi surface. Since the antiferromagnetic long range order is present, the Brillouin zone is halved in the AF1 and AF2 phases. The lower band is completely full, while the upper band is partially filled. The Fermi surface of the AF1 phase has a hole pocket, and it has an electron pocket in the AF2 phase. The hole-like Fermi surface of the AF1 phase can be obtained by folding the Fermi surface in the PKS phase. Therefore the AF1 phase and the PKS phase are smoothly connected with each other, the phase transition between the two phases is of second order. The Fermi surface topology in the AF2 phase is different, thus the transitions from the AF2 phase to the other two phases are of first order. Since the model has particle–hole symmetry at half filling, the difference between the AF1 phase and AF2 phase disappears.
4. ConclusionIn summary, we applied the density matrix embedding theory to the two-dimensional periodic Anderson model. We mainly concentrated on the ground state properties. We systematically investigated the phase transitions between the AF2 phase, AF1 phase, and PKS phase. The phase transition from the AF1 phase to PKS phase is just the ordinary magnetic transition, while the phase transitions from the AF2 phase to the other two phases are of first order, which are accompanied by a Fermi surface reconstruction. We obtained the V–Ef phase diagrams at different fillings, and found that as the filling is getting close to the half filling, the AF2 phase is shrinking while the AF1 phase is expanding. In order to characterize different phases, we computed the local magnetic moments as well as the short-range spin–spin correlation functions. There are regions where the antiferromagnetic long-range order presents, as the magnitudes of the local moments on both c and f orbitals are decreasing, while the absolute value of the spin–spin correlation function is increasing. This indicates that the AF order coexists with the Kondo singlet phase. We further compared the local magnetic moments at different fillings, and discovered that the difference of the AF2 phase and AF1 phase is disappearing as we approach the half filling. This behavior is similar to the water liquid–vapor transition. Before the critical point, the phase transition between the liquid phase and gaseous phase is of first order. The difference of the two phases is the density. However after the critical point, the densities of the two phases become the same, there is no way to distinguish them. The AF2 phase and AF1 phase are just like the liquid water phase and the gaseous water phase. The phase transition of the AF2 phase and AF1 phase is not accompanied by any symmetry breaking. There exists a quantum critical point at half filling or quite close to half filling.