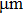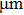† Corresponding author. E-mail:
Ultrafast imaging tools are of great importance for determining the dynamic density distribution in high energy density (HED) matter. In this work, we designed a high energy electron radiography (HEER) system based on a linear electron accelerator to evaluate its capability for imaging HED matter. 40 MeV electron beams were used to image an aluminum target to study the density resolution and spatial resolution of HEER. The results demonstrate a spatial resolution of tens of micrometers. The interaction of the beams with the target and the beam transport of the transmitted electrons are further simulated with EGS5 and PARMELA codes, with the results showing good agreement with the experimental resolution. Furthermore, the experiment can be improved by adding an aperture at the Fourier plane.
High energy density (HED) matter is usually defined as matter in the state of deposited energy larger than 1011 J/cm3 or, equivalently, pressure higher than 1 Mbar. This state of matter is widespread in the universe stars and centrosphere. Furthermore, HED matter is also an important state for the inertial confinement fusion (ICF) processes. The physical properties of the matter at the extreme states are the most interesting for high energy density physics (HEDP) research: for instance, the knowledge of spatial distribution and temporal evolution of the temperature, volume, pressure, and density of HED matter are required for conducting experiments. In ICF/HEDP research, the fuel capsule density can be varying dramatically, from 0.02 g/cm3 to 400 g/cm3, with the spatial scale strongly compressed from 3 mm to 
Many ultrafast imaging diagnostic tools are based on the use of hard x-rays, Gamma rays, electrons, protons, and carbon beams, or even neutron beams produced by high power lasers or other pulsed power devices.[1–10] High energy proton radiography developed at Los Alamos National Laboratory (LANL) has shown its great potential for HED matter diagnostics with excellent spatial and temporal resolutions.[11–13] This technique is also proposed at the Facility for Antiproton and Ion Research (FAIR) with 4.5 GeV proton beams.[14,15] Although a proton beam is superior to an electron beam in terms of penetration ability, a high energy proton accelerator and the corresponding imaging system are very costly, and a ps-scale proton beam bunch with desirable energy and intensity for radiography is not yet available in the laboratory. In addition, a proton radiography facility is always much larger in size than an electron radiography system. Furthermore, many other diagnostic methods, e.g., using the runaway electrons, are also applied to study the plasma characteristics.[16]
High energy electron radiography (HEER) is important to implement experimentally because of the great potential in the diagnostics of HED matter. So far, the reported radiography has achieved 
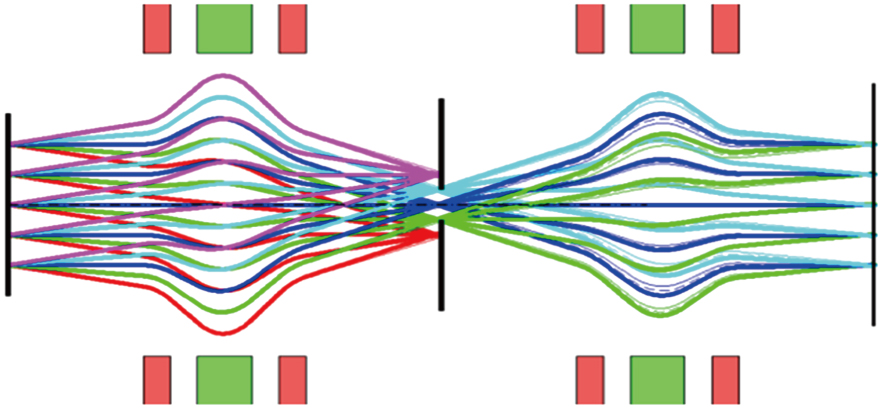
The high energy short pulsed electron beams have energy spreading and angle scattering after passing through the specimen. The electrons with angle and energy distributions can be refocused on the screen by the magnetic lens system. The electrons arrived at the area on the screen are the electrons emitted by the corresponding area on the target, thereby enabling point-to-point imaging. The intensity of photons is proportional to the electron count on the screen; thus, different intensities show the areal density distribution from the corresponding location. The chromatic aberration of the electron beams can be reduced by using an aperture at the Fourier plane of the magnetic lens. Figure
Two key aspects for the HEER application to HED matter diagnostics, namely spatial resolution and density resolution, are investigated in this paper. Related to the spatial resolution, the deviation of the electrons on the screen dominates in the point-to-point imaging technique. The deviation of electrons can be described by the following formula:
 |

The interaction of high energy electron beams with materials is very complex. However, only the multiple scattering, ionization, and bremsstrahlung processes need to be considered in our case. For high energy electrons, Coulomb scattering introduces a certain distribution when the electrons are travelling in the target. The energy loss experienced by the electrons is mainly due to the bremsstrahlung and ionization processes.
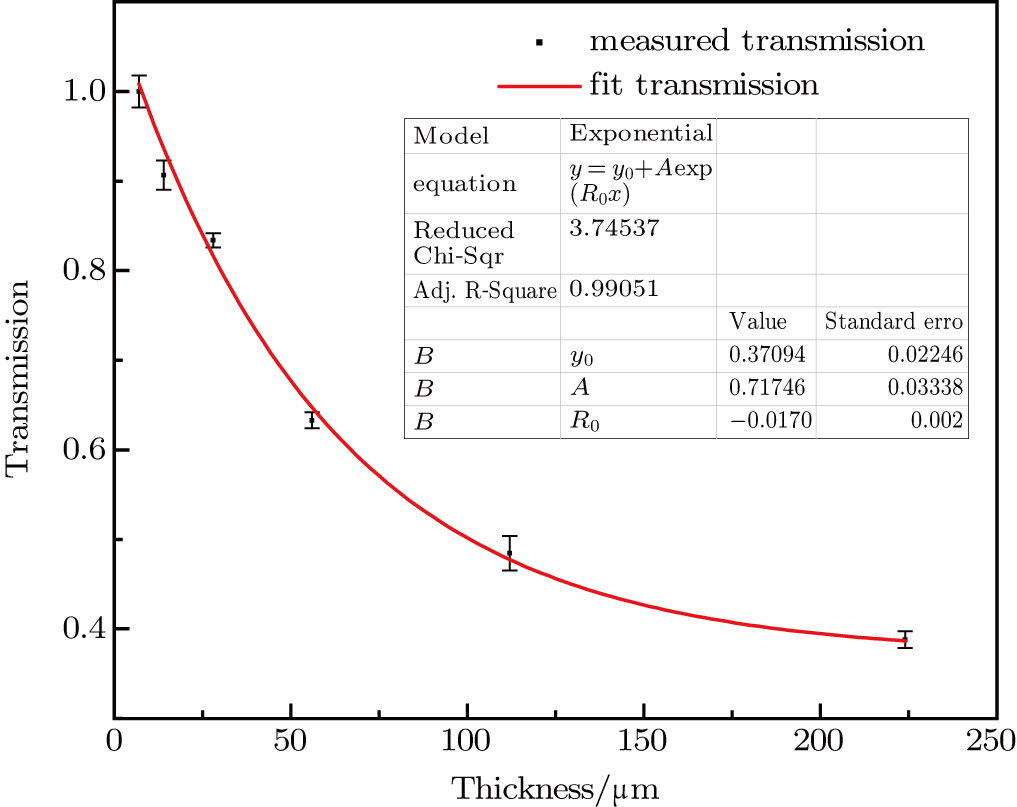
All the processes related to the electron beam going through the target and transported in the beam line will result in a loss of electrons. The transmission of the monoenergetic electron beam going through the target as a function of the target mass thickness can be given by a binomial formula.[19] Therefore, the areal density can be extracted from the transmission. Meanwhile, the transmission relates to the initial energy of the electron beam. For the point-to-point imaging system, the transmission is also influenced by the settings of the beam line. The scattering angle plays an important role in the imaging quality. Molière’s multiple scattering theory gives the distribution of the electrons scattering angle after the target, which can be written in the following way:
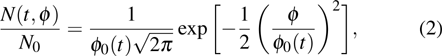 |
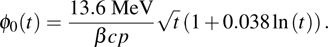 |
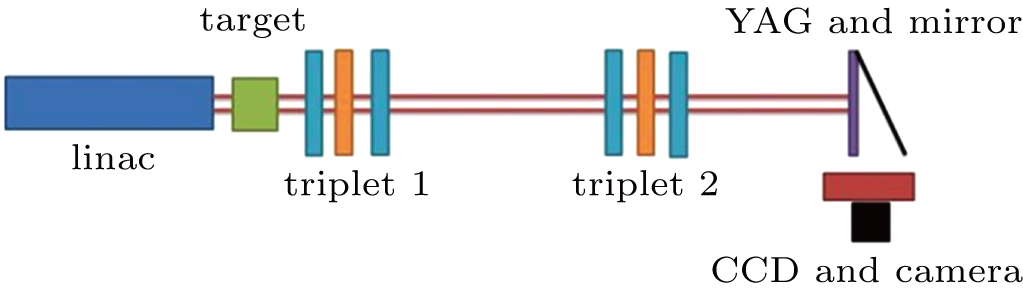
The HEER system was commissioned at the THU linear electron accelerator. The electron beam and lens system are designed as shown in Fig. 
A step-wise aluminum target used as the sample was placed at the object plane; the thicknesses of the six steps were 7, 14, 28, 56, 112, and 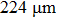
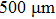
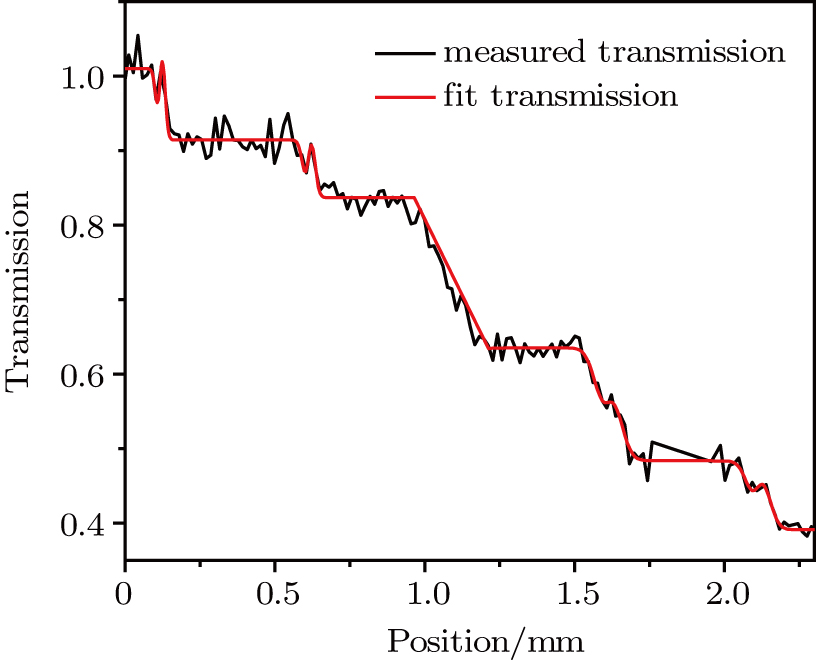
The recorded image of the Al ladder target is shown as Fig. 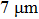
| Table 1.
RMS spatial resolution of the 46.2 MeV HEER experiment. The RMS width is obtained from the fit line shown in Fig. |
The transmission of each step can be found by fitting the line in Fig.
Simulations were performed to study the influence of the aperture size at the Fourier plane on HEER.
In simulations, we calculated the delivery of electrons that hit the target and later propagate in the magnetic field and refocus on the screen. There are two specific processes that were considered in the simulations: the EGS program was used to calculate the interaction between the 40 MeV electron beams and the aluminum stepwise target that we used in the experiment; the other process is the electron transport in the two triple-magnet lens system after the target simulated with the PARMELA code.[20,21] The influence of the aperture size at the Fourier plane on HEER is discussed theoretically.
The distribution of the electrons at the Fourier plane can be described by the following formula:
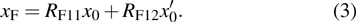 |
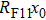
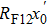
 |
| Table 2.
Transfer matrix of the origin to focus. . |
| Table 3.
Parameters of the lattice. . |
Figure
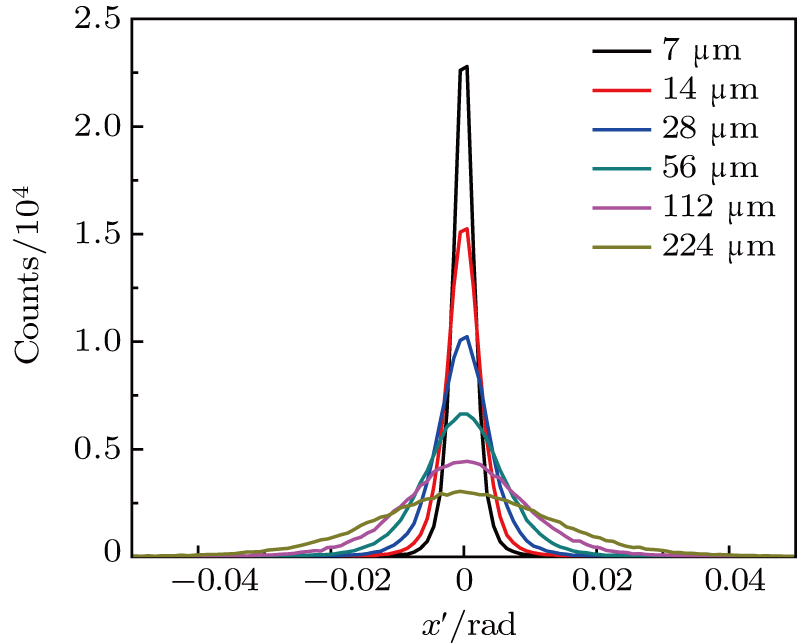 | Fig. 7. (color online) Angle distribution of the electrons after passing through the target with varying thickness. |
| Table 4.
Sigma of the Gaussian function fitting the angle distribution. . |
| Table 5.
RMS spatial resolution obtained in the 40 MeV HEER simulations. The block letters in Table |
In this work, 
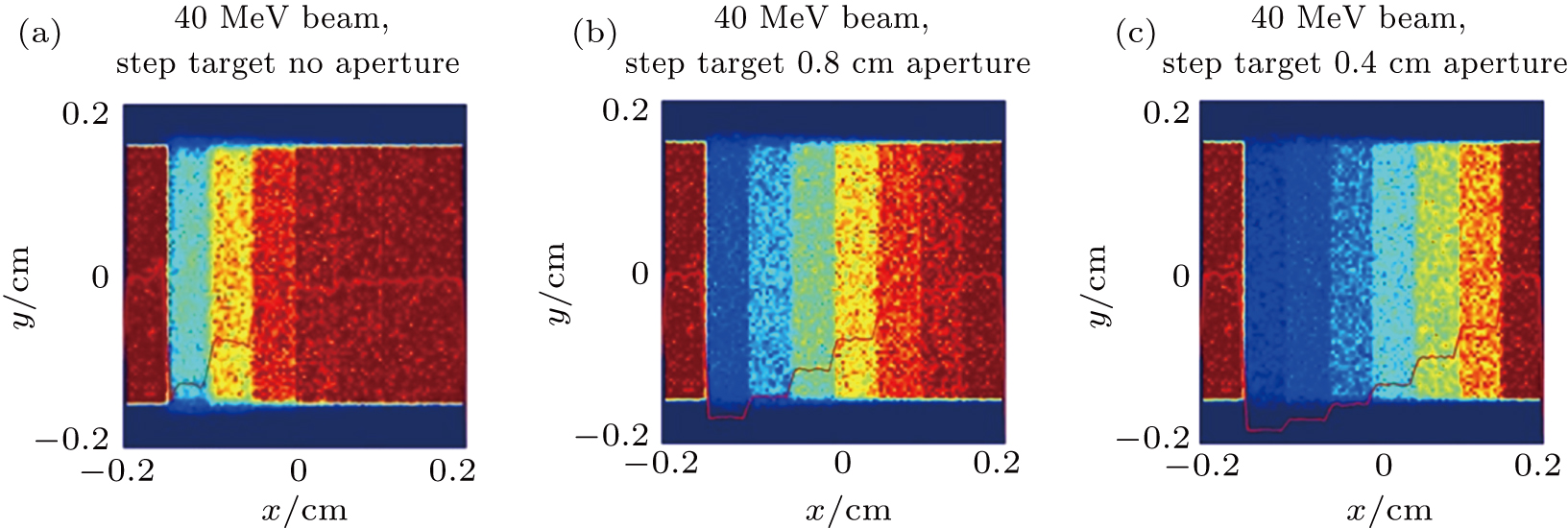
Using apertures of different size at the Fourier plane, we simulate the images shown in Fig.
Figure
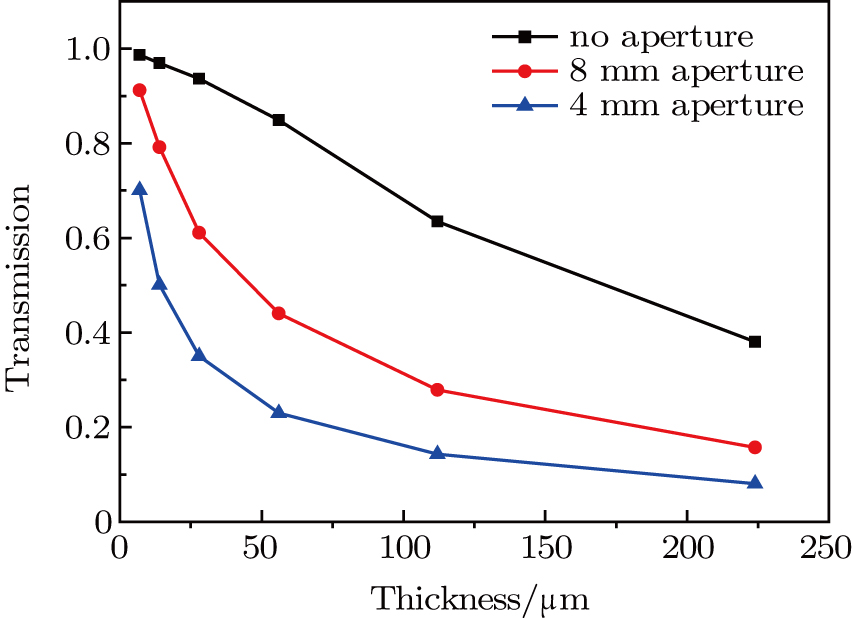 | Fig. 9. (color online) Transmission across each step for the cases of no aperture (black), 8 mm side length aperture (red), and 4 mm side length aperture (blue) at the Fourier plane. |
The distribution of the electrons on the screen is shown in Fig.
The experimental result of radiography measurements using the 46.2 MeV electron beams agrees well with the simulations for 40 MeV HEER on an aluminum step target, giving the RMS spatial resolution on the order of tens of micrometers. The transmission of the electron beams for different areal densities were investigated experimentally. The influence of the diameter of the aperture placed at the Fourier plane was discussed, showing that smaller apertures can improve the spatial resolution to several micrometers and make the transmission more sensitive to the areal density. In summary, the result of the experiment is consistent with the simulations, demonstrating that the LINAC with an ultra-short pulsed electron bunch is suitable for HEER applications.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] |