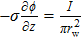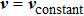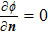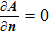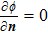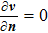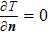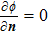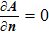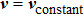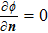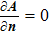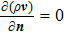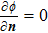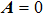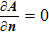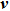† Corresponding author. E-mail:
The physical characteristics of a plasma arc affect the stability of the keyhole and weld pool directly during keyhole plasma arc welding (KPAW). There will be significant change for these characteristics because of the interaction between the keyhole weld pool and plasma arc after penetration. Therefore, in order to obtain the temperature field, flow field, and arc pressure of a plasma arc under the reaction of the keyhole, the physical model of a plasma arc with a pre-set keyhole was established. In addition, the tungsten and base metal were established into the calculated domain, which can reflect the effect of plasma arc to weld pool further. Based on magneto hydrodynamics and Maxwell equations, a two-dimensional steady state mathematical model was established. Considering the heat production of anode and cathode, the distribution of temperature field, flow field, welding current density, and plasma arc pressure were solved out by the finite difference method. From the calculated results, it is found that the plasma arc was compressed a second time by the keyhole. This additional constraint results in an obvious rise of the plasma arc pressure and flow velocity at the minimum diameter place of the keyhole, while the temperature field is impacted slightly. Finally, the observational and metallographic experiments are conducted, and the shapes of plasma arc and fusion line agree with the simulated results generally.
Welding with penetration of plasma arc is an ideal method to join thick metal plate because it can weld one pass with backside formation.[1] To compare with other high energy beam welding, keyhole plasma arc welding method (KPAW) has the advantages of low cost and easy operation. However, the stability of KPAW will become weak as the welding current increases and some welding defects will appear because of the unstable plasma arc with strong penetrating force. Moreover, there is a violent interaction among plasma arc, weld pool, and keyhole, which can make the physical characteristics change complicatedly. Similar to the compressed effect of nozzle, the keyhole causes an additional constraint to plasma arc. Arc pressure, velocity, and temperature become more complex under the additional constraint effect. Furthermore, the formation and stability of keyhole weld pool are affected. So it is helpful for better understanding the KPAW process by investigating the physical characteristics of plasma arc and weld pool under the additional constraint effect of the keyhole.
Numerical simulation has been an effective method to study the welding process because the computer technology and numerical theory develop rapidly. Regarding to the simulation of welding arc, early articles mostly focused on the solution of arc region without considering the electrode, base metal, and their interactions.[2–5] Then, in order to avoid the artificial assumption of welding current on the tungsten tip, a fluid and solid coupling calculation was conducted by considering tungsten into the calculated domain.[6] Based on the previous models, including energy source terms on surfaces of electrode and base metal, the unified calculated models were established to analyze the heat and mass transfer between arc and base metal.[6–14] Subsequently, researchers began to use these models to study more complex factors which influenced the physical characteristics of welding arc. Fan et al.[15] presented a three-dimensional model of tungsten inert gas welding arc taking the behavior of metal vapor into account. Zhou et al.[16] numerically analyzed the influence of the surface topography of the deposited layer on arc in additive forming process. Through the above study of free arc, researchers has understood the mechanism of heat generation, distribution of arc physic field and energy transfer deeply.
However, for KPAW, modeling and calculation are more complicated because of the severe physical characteristics and keyhole effects. The special keyhole digging process of KPAW has been numerically analyzed by tracking the free surface of weld pool. The evolution of temperature and flow field in weld pool was quantitatively investigated by coupling keyhole deformation and thermal-mechanical effects.[17–20] Jian et al. and Pan et al.[21,22] developed a unified model of plasma arc welding by coupling the transport behavior between plasma arc and weld pool. The whole region consisted of the plasma arc, and weld pool, and the keyhole penetrating process was simulated at the same time. Moreover, Li et al.[23] established a more effective calculated model of KPAW by pre-set a simple keyhole to study the thermo-physical process.
Even though there have been a lot of study about KPAW, the evolution of the whole physical field under the additional constraint effects of a keyhole with efflux has not been investigated. Under the action of keyhole penetration, it is significant to control the formation of a back side weld bead. After full penetration, there is one more outlet for arc plasma, which has a serious impact on arc physical characteristics. Conversely, the plasma arc can affect the weld pool further. Therefore, for numerical analysis of KPAW, it is very necessary to establish a unified model including electrodes, plasma arc, and efflux to study the heat and force transfer in a more complete region. In this work, considering the interaction law on the cathode and anode, a unified model coupling plasma arc, weld pool, keyhole, and efflux is proposed to study the physical field in quasi-steady state of KPAW. Through this study the numerical model will be improved and it is also helpful to understand the transport phenomenon in KPAW further.
Figure
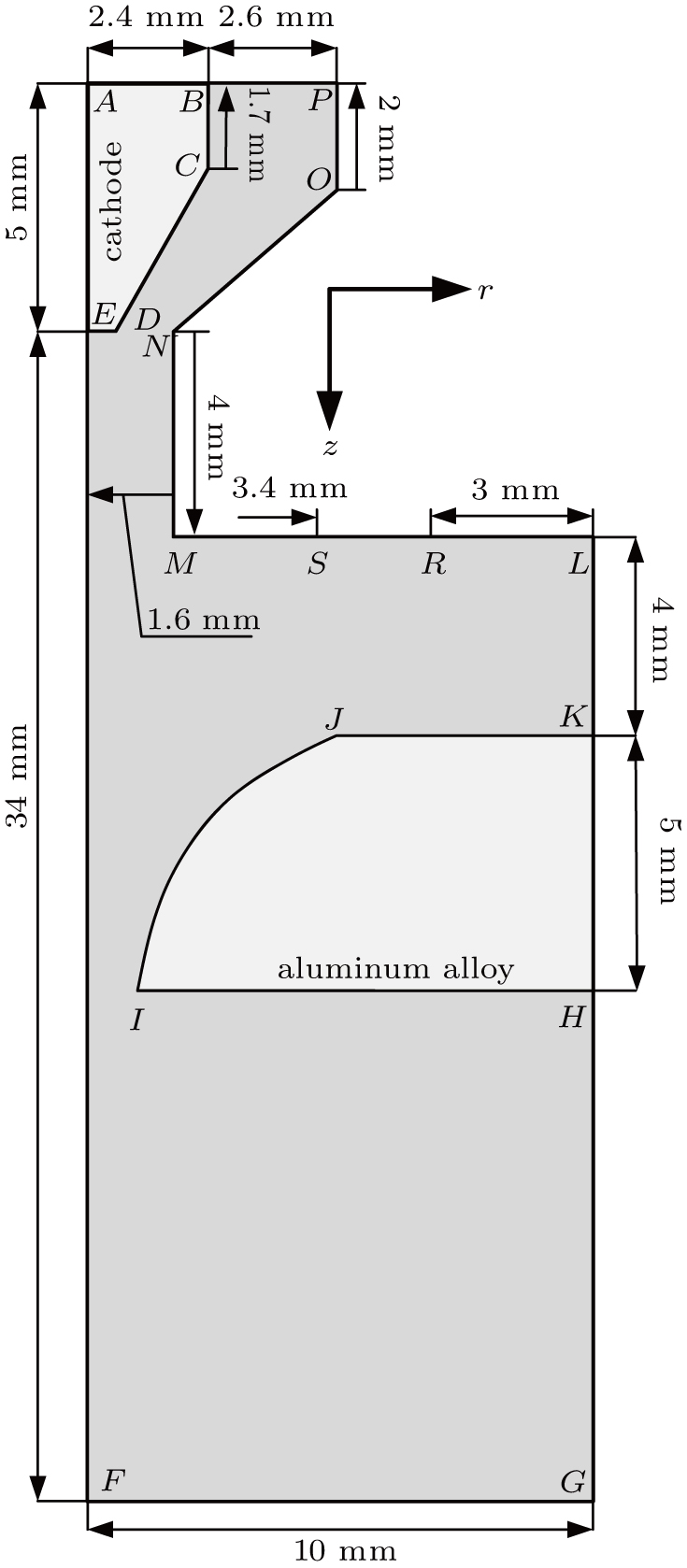
The conditions used in the simulation are the same as those in experiments. Plasma gas and shielding gas are both argon. The flow rates are 2.0 L/min and 15 L/min, respectively. The welding current is 140 A. Arc length, the distance from ML to JK, is 4 mm.
To mathematically model the arc, pool, and the interaction, we assume that (i) the plasma arc is in local thermodynamic equilibrium, (ii) the fluid is laminar, and (iii) the plasma arc is a continuous medium. The simplifications are made that (i) the viscous dissipation is neglected, (ii) the plasma arc is axisymmetric, and (iii) the metal vapor and fluid flow inside the weld pool are neglected. The direction of the gravity is the positive of the z axis. The latent heat of the metal evaporation is neglected.
Based on the above assumptions, the governing equations are described as
(i) mass conservation:
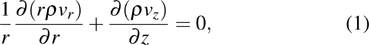 |
(ii) radial momentum conservation:
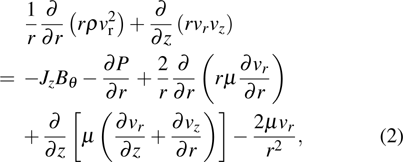 |
(iii) axial momentum conservation:
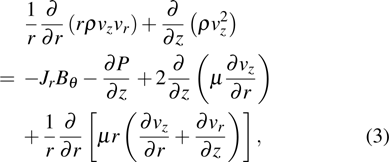 |
(iv) energy conservation:
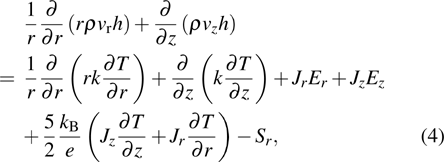 |
There is the term of Lorenz force in momentum conservation and Joule heat term in energy conservation. So the Maxwell equations need to be solved to get the distribution of magnetic induction B and current density J, which is shown as
Ohmʼs law:
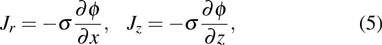 |
 |
 |
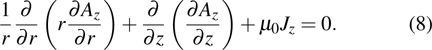 |
 |
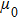
An additional energy source term which can describe the thermal and flux that occurs only at the electrode is needed. The additional heat flux at the cathode includes thermionic cooling, ion heating, and radiation cooling, which is defined as
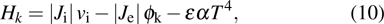 |
 |
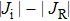
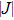
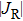
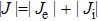
At the anode surface, it also needs an additional energy source term of heating by electron condensation and radiation cooling, which is written as
 |
The boundary condition is set according to the actual welding process as shown in Table
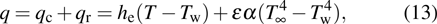 |
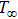
| Table 1.
Boundary conditions. . |
Figure
Figure
Figure
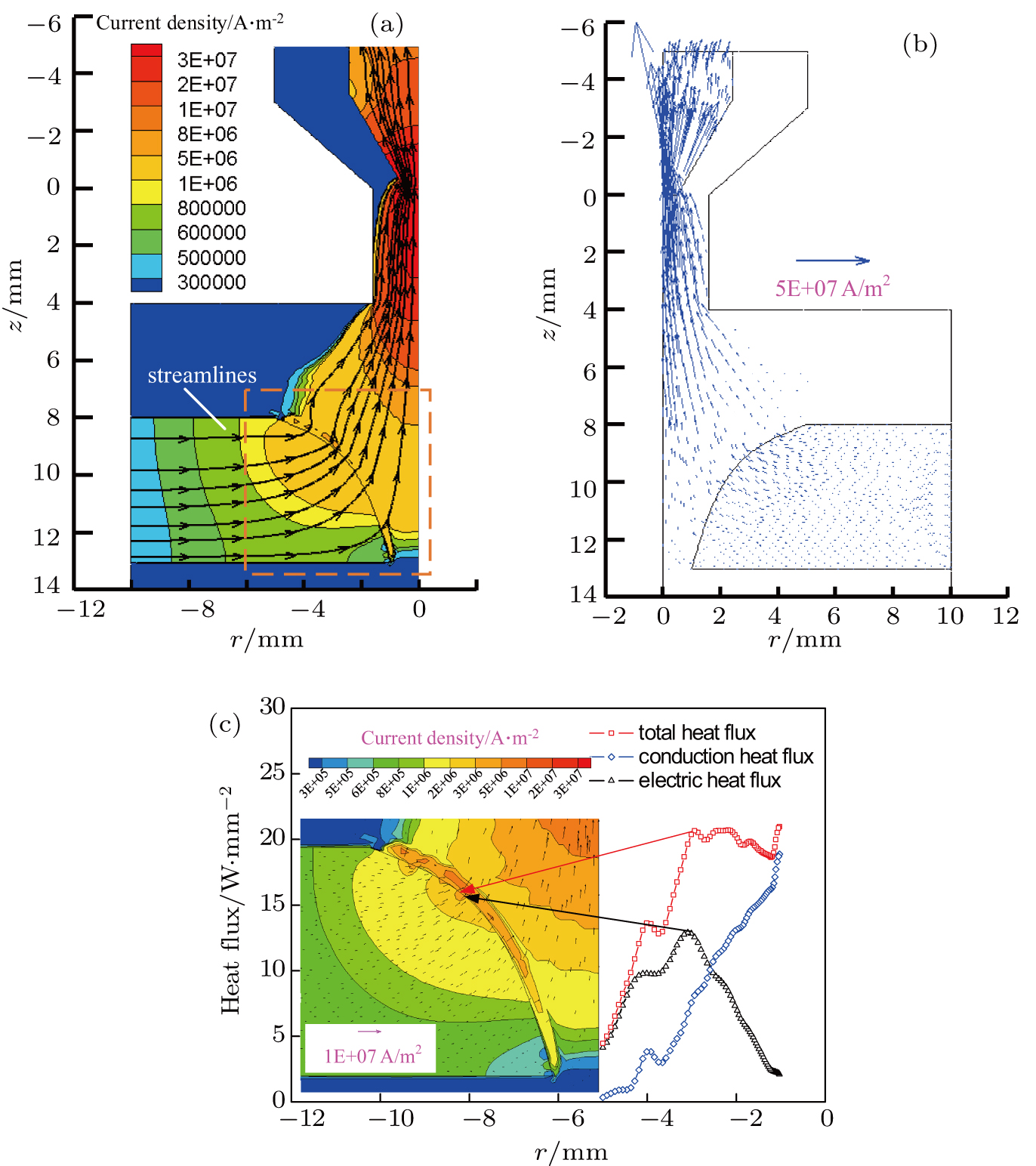 | Fig. 4. (color online) Distribution of current density and heat flux on the keyhole boundary. (a) Distribution contour and flow direction, (b) vector, and (c) heat flux. |
Figure
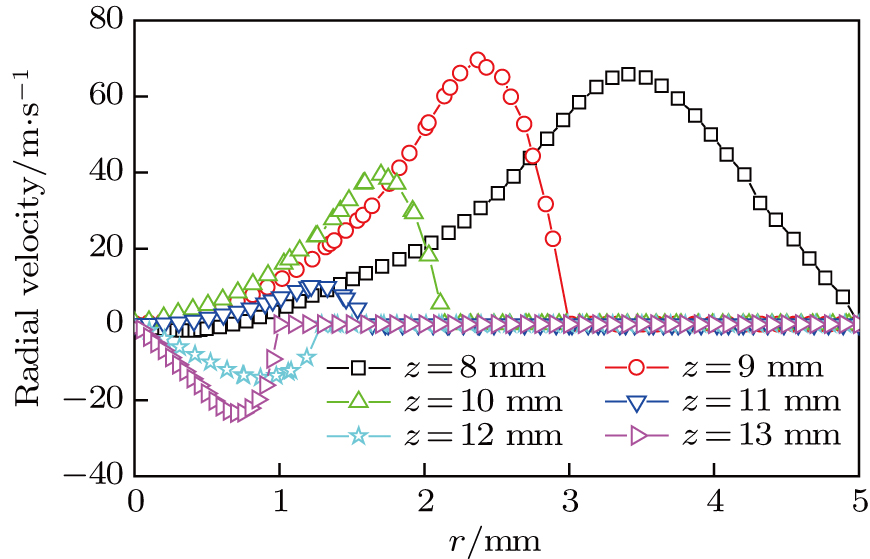
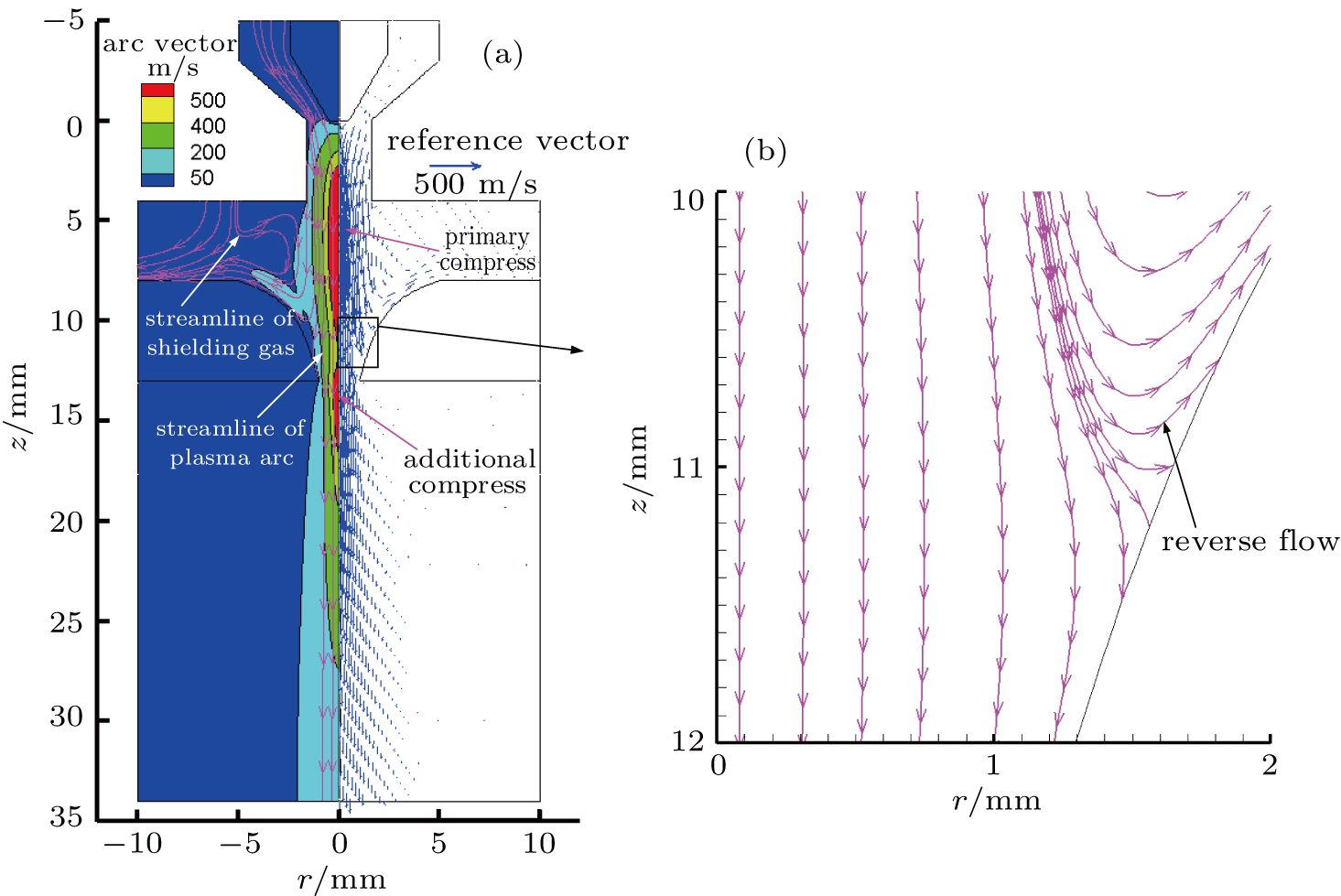 | Fig. 5. (color online) Velocity distribution of plasma arc and its vector. (a) Velocity in the whole region and (b) magnified reverse flow region. |
Figure
Figure
Figure
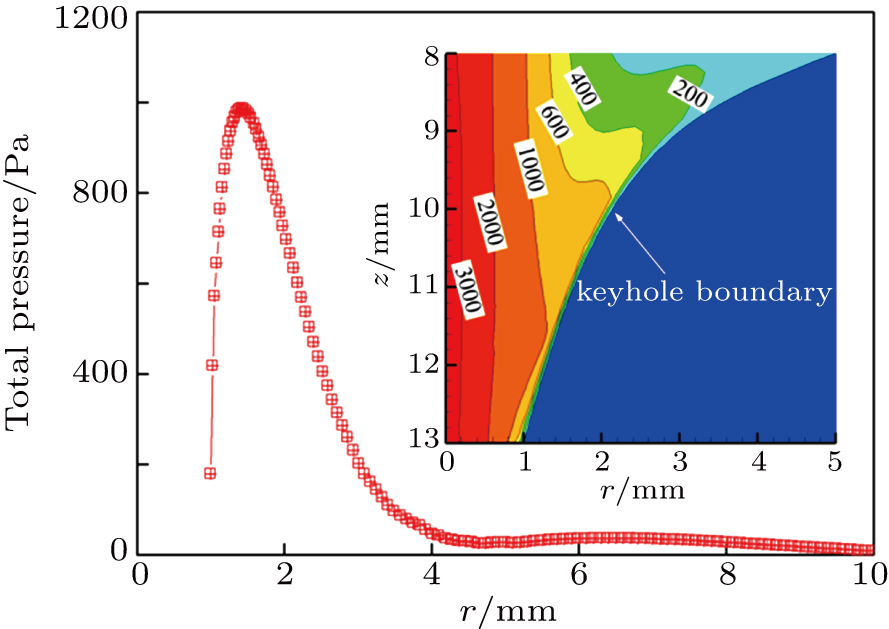
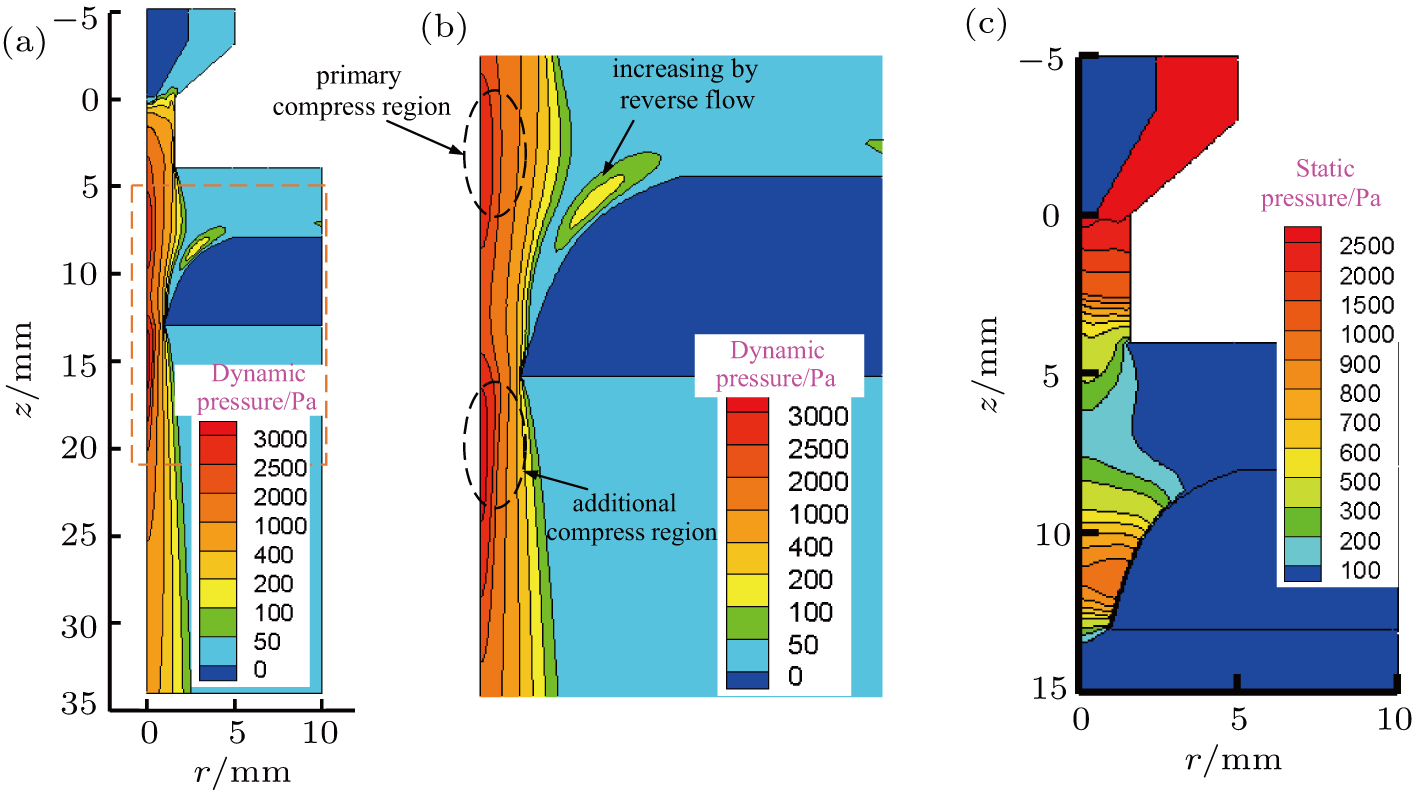 | Fig. 8. (color online) Distribution of plasma arc pressure. (a) Dynamic pressure in the whole region, (b) magnified compressed region, and (c) static pressure distribution. |
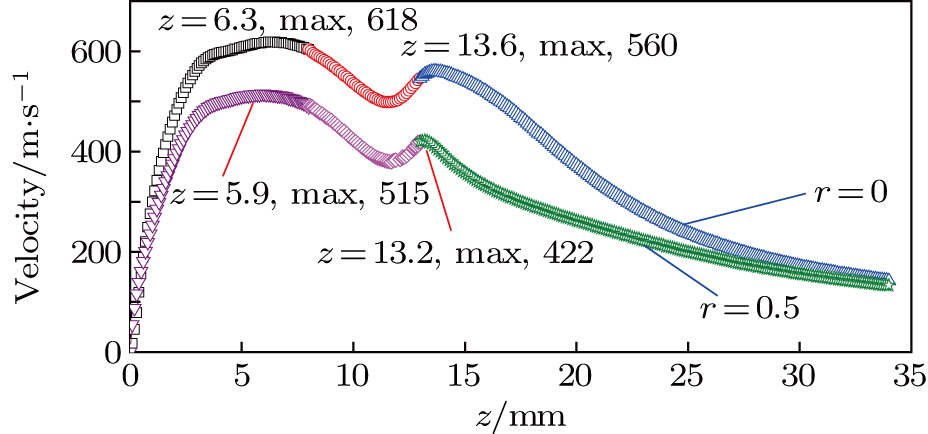
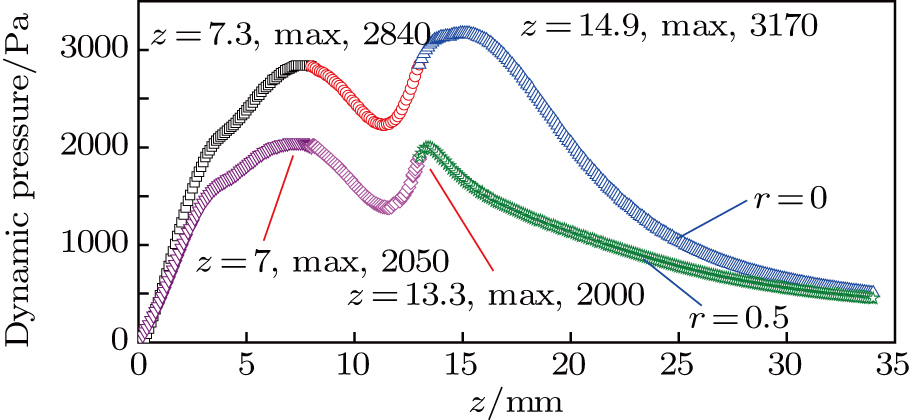
Similar to the distribution of velocity on the axis line, dynamic pressure reaches to a two peak value under the constraint of nozzle and keyhole. Respectively, on lines of r = 0 and r = 0.5 mm, the peak values are shown in Fig.
Figure
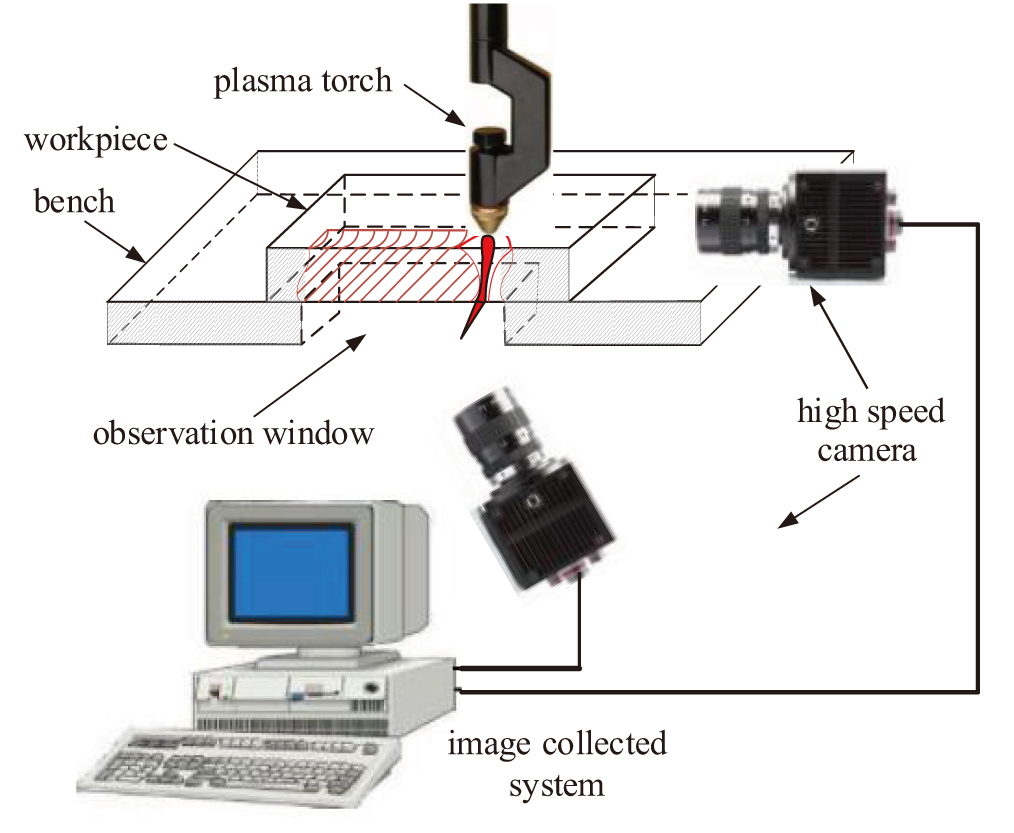
A high speed camera experiment platform is built to verify the calculated model, which is shown in Fig. 
Figure
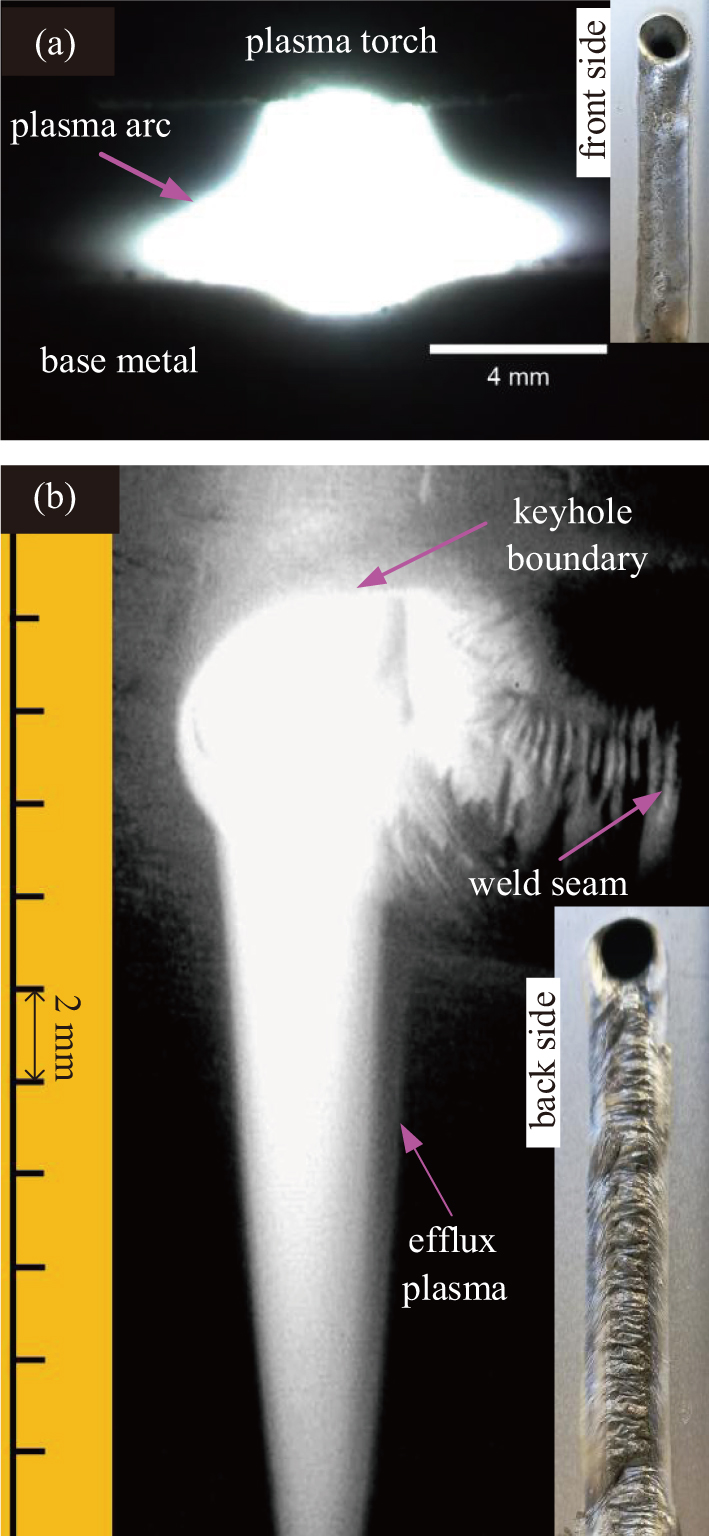 | Fig. 12. (color online) Images of (a) plasma arc of front side and (b) efflux plasma of bottom side. |
Therefore, from the shape and size of plasma arc and efflux, it preliminarily indicates that the calculated model is reasonable.
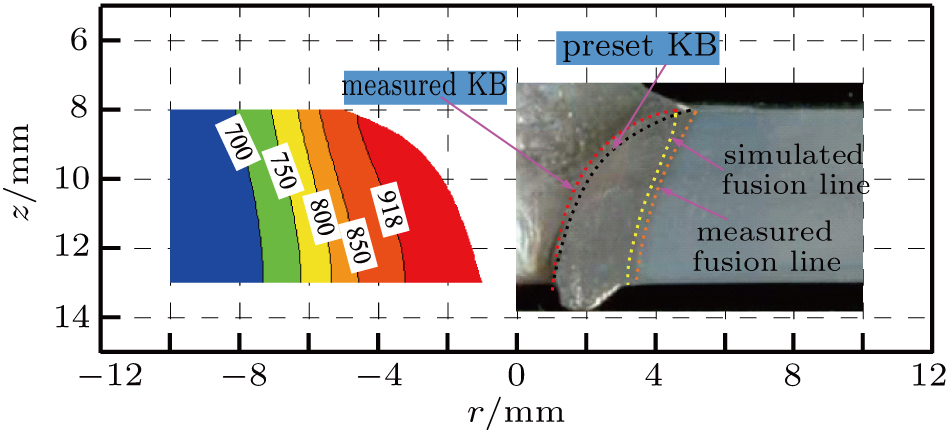
In addition, a plasma arc penetrating experiment was performed and the macrograph of the weld was made. Comparing the simulated and experimental results, it is shown that the fusion zone and keyhole size are in good agreement with each other, as shown in Fig.
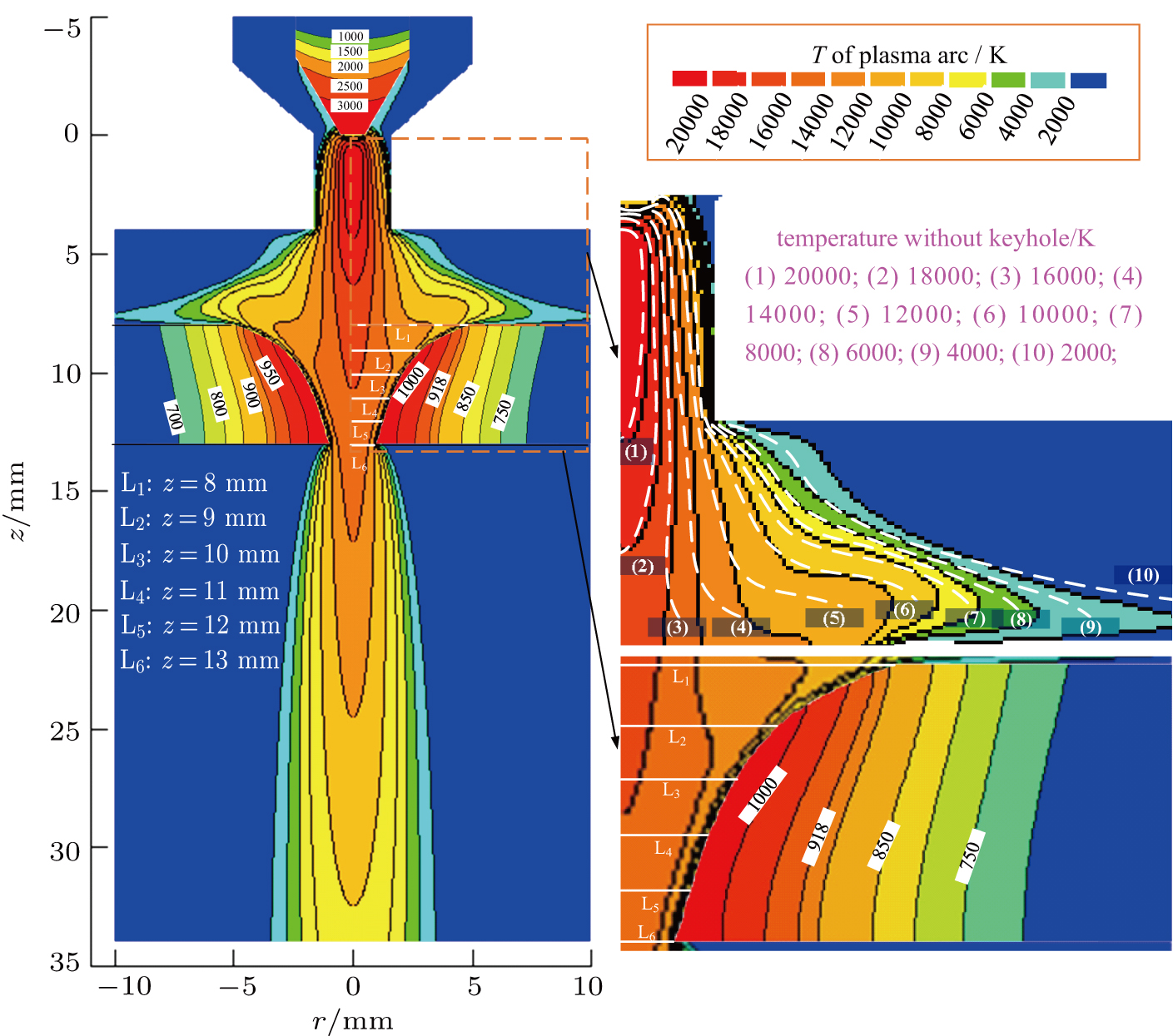
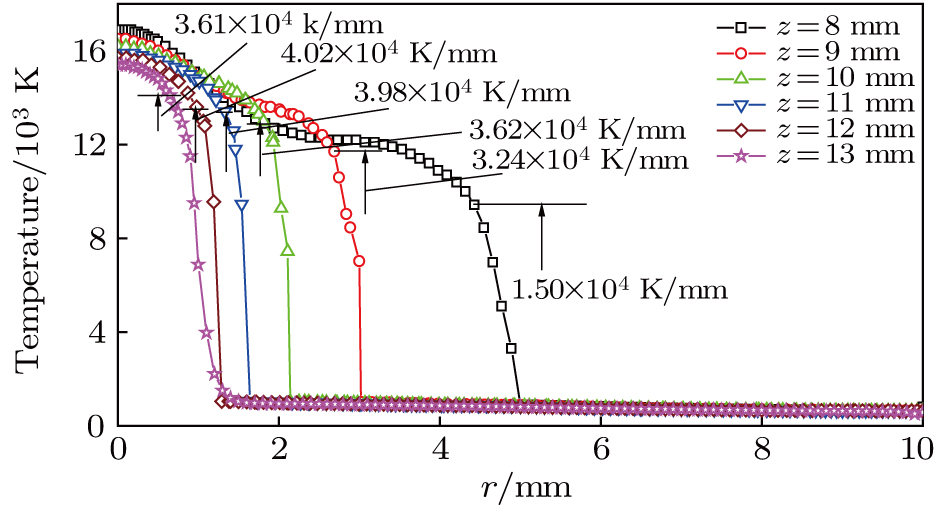
The plasma arc temperature on the upside of base metal with a keyhole relatively shrinks to the center more than that without keyhole. The arc temperature gradient on the boundary increases as the depth of keyhole and decreases when close to the bottom of the keyhole.
The welding current mainly flows through the upper part of the keyhole. The heat on the upper part of the weld pool is produced both by electronic heat and heat conduction, while that on the lower part is provided mainly by heat conduction.
The second peak of arc pressure appears on the axis under the additional constraint of the keyhole. Plasma velocity has a similar characteristic with arc pressure and reverse flow occurs near the keyhole boundary.
Comparing the results of simulation and experiments, the shapes of weld, plasma arc, and efflux plasma are basically in agreement with each other.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] |