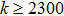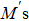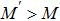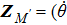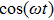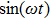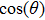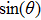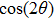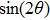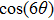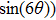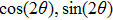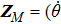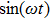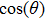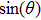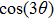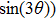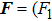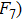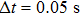† Corresponding author. E-mail:
Nowadays, massive amounts of data have been accumulated in various and wide fields, it has become today one of the central issues in interdisciplinary fields to analyze existing data and extract as much useful information as possible from data. It is often that the output data of systems are measurable while dynamic structures producing these data are hidden, and thus studies to reveal system structures by analyzing available data, i.e., reconstructions of systems become one of the most important tasks of information extractions. In the past, most of the works in this respect were based on theoretical analyses and numerical verifications. Direct analyses of experimental data are very rare. In physical science, most of the analyses of experimental setups were based on the first principles of physics laws, i.e., so-called top-down analyses. In this paper, we conducted an experiment of “Boer resonant instrument for forced vibration” (BRIFV) and inferred the dynamic structure of the experimental set purely from the analysis of the measurable experimental data, i.e., by applying the bottom-up strategy. Dynamics of the experimental set is strongly nonlinear and chaotic, and itʼs subjects to inevitable noises. We proposed to use high-order correlation computations to treat nonlinear dynamics; use two-time correlations to treat noise effects. By applying these approaches, we have successfully reconstructed the structure of the experimental setup, and the dynamic system reconstructed with the measured data reproduces good experimental results in a wide range of parameters.
In recent years, a large scale of data has been accumulated in various fields, especially in social and biological systems.[1–4] However, the system structures generating these data are usually not clear.[5,6] Therefore, it is very important in interdisciplinary fields to reveal system structures by analyzing their output data, called dynamic structure reconstructions.[7–13] A typical example in this regard is a recent dialogue project on reverse engineering assessment and methodology (DREAM), which has attracted considerable attention in the field of reconstructing gene regulatory networks.[14,15] Similar objectives are found in other areas, such as neural networks[16,17] and ecosystems.[18] Mathematically, dynamics of systems considered are widely described as coupling ordinary differential ODEs[19–22] and the problem of system reconstructions is thus to reveal these linear or nonlinear structures of the differential systems. So far, many system structures’ reasoning methods had been proposed to different fields to solve various structure reconstruction problems.[15,23–27] In most of the practical cases, network reconstructions from measurable data must encounter some major difficulties: nonlinearity of network dynamics; and effects of unknown impacts, such as noise. The joint interplay of these difficulties makes the problem of network reconstructions challenging. In order to overcome these difficulties, some new integrated physical thinking and intelligent methods have been proposed.[15,23–34] So far, most of the works of network reconstructions have considered mathematical analyses and numerical simulations of various models, and much fewer works directly analyzed realistic experimental data. Moreover, a majority of works of network reconstructions are in the social and biological disciplines. In physics, scientists have been familiar with research strategies, starting from the first principles, i.e., so-called top-down analyses, and people have very seldom inferred structures of experimental setups by analyzing measurable data of experiments only. Due to some unknown complexities of experimental sets; unknown experimental surrounding; and strong nonlinearity and chaotic of dynamics, the conventional top-down strategies are not always successful, and direct analyses of experimental data, i.e., the bottom-up strategies, may serve as useful tools to reconstruct experimental structures. In this paper, we collect data of oscillating angle of the Boer resonant instrument under forced vibration with a very high measurement frequency and try to reveal the dynamical structure of the experimental set purely from measurable data. For performing effective data analysis, we use high-order correlations to treat nonlinearity of the experimental system, and two-time correlations to deal with noises existing in the experiment. Then by analyzing the available angle data only, we are able to infer the interaction structures between different experimental subsets; fix some unknown and not measurable physical parameters, and reconstruct the dynamic model of the experimental system. In particular, the reconstructed mechanical model can satisfactorily reproduce essential dynamic features in a wide range of control parameters, though the data under analysis are taken from the experimental measurement at a fixed single parameter set.
In this paper, we conduct an experiment of “Boer resonant instrument for forced vibration”, i.e., we use a fine iron bar with a matching nut adding on a Pohlʼs torsion pendulum to complicate the apparatus,[35] and further, introduce a double-well potential into the basic torsion pendulum apparatus. This experimental setup can produce very rich experiment results such as complicated patterns of periodic and chaotic motions and diverse bifurcations between these patterns, by varying a single experimental parameter, the frequency of the driving force, only.[36–39]
Pohlʼs torsion pendulum is a torsional harmonic oscillator that can oscillate with a rotational motion about the axis of a torsion spring clockwise and counterclockwise. Its behaviors are analogous to those of translational spring-mass oscillators, and the corresponding linear iZed equation of the copper rotating wheel is accepted for describing its dynamics, which is
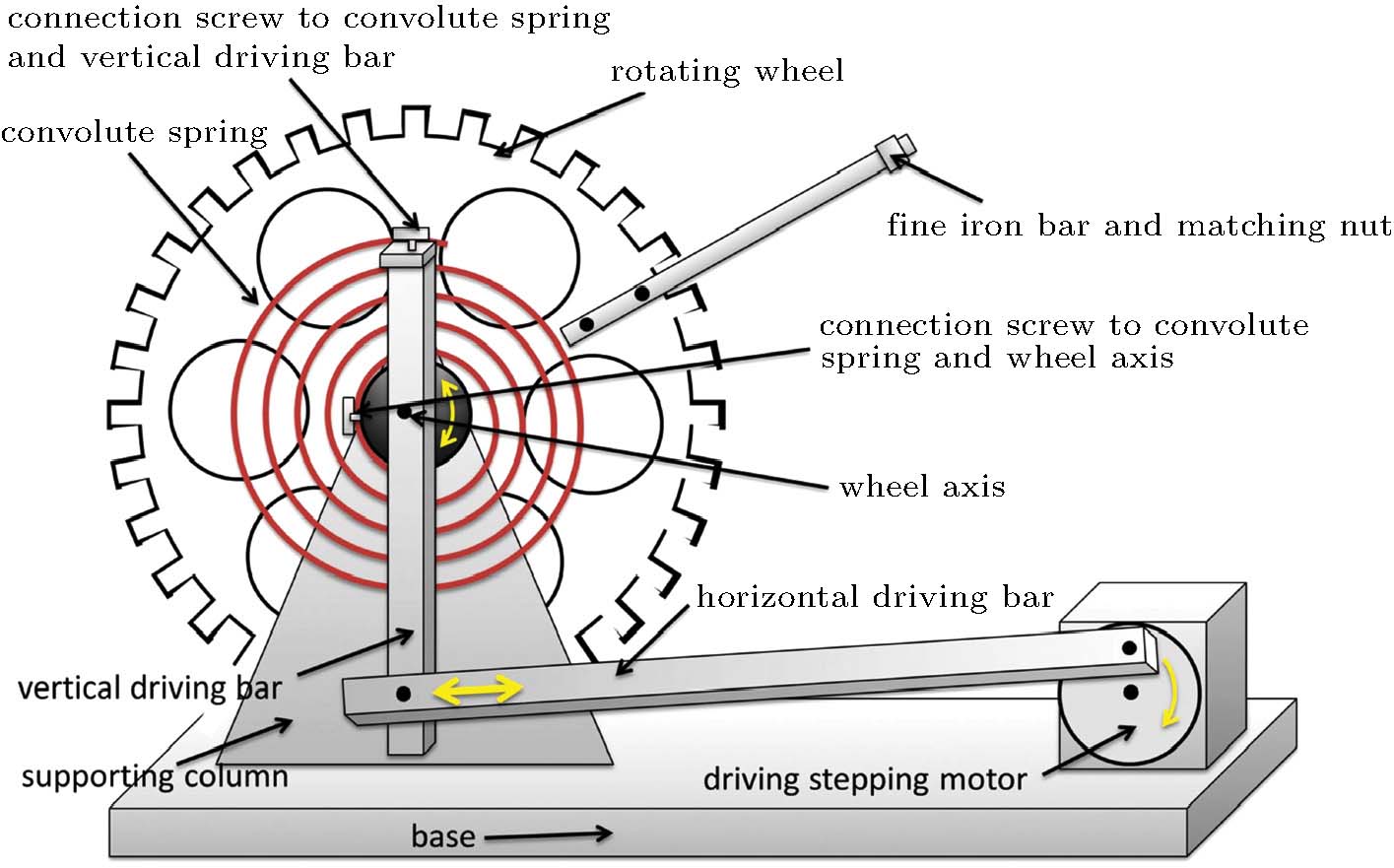 | Fig. 1. (color online) Experimented setup of “Boer resonant instrument for forced vibration”,[35] a fine iron bar with a matching nut is added to a Pohl’s torsion pendulum, and a double-well potential structure is introduced by a torsion pendulum apparatus through adding weights to the copper rotating wheel of Pohl’s torsion pendulum basis. Extremely rich experiment results can be explored in the torsion pendulum experiment, including rich patterns of periodic and chaotic motions and diverse bifurcations between these patterns, by varying a single experimental parameter, the frequency of the driving force, only. |
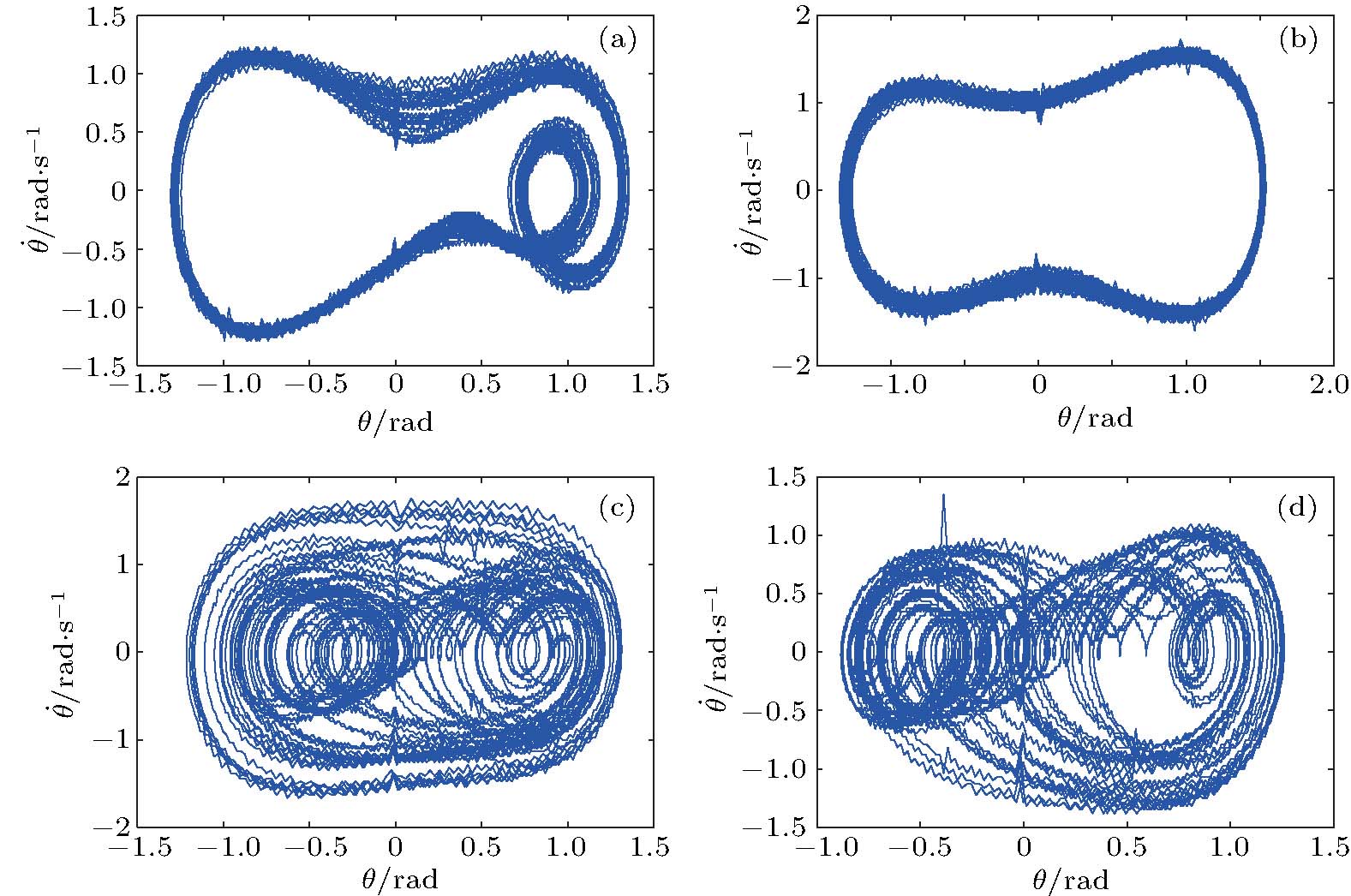
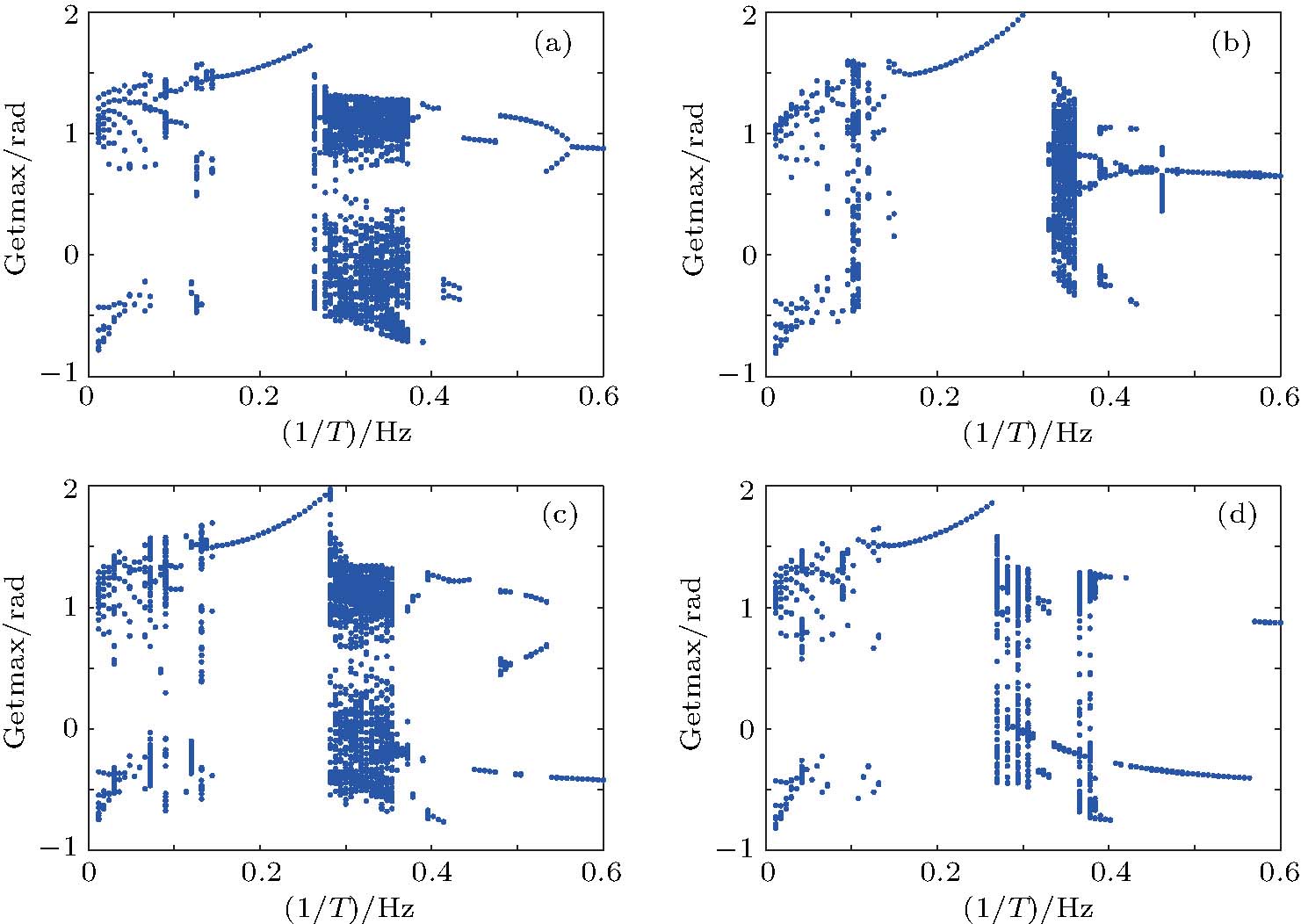
In all experiments, the data of swing angle θ are measured by an organic glass turntable and collected. The frequency of measurements are very high as fm=50 Hz, and the duration of angle measurement is rather long up to L = 7200 s, so that all behaviors of different types of motions can be well captured. By recording the swing angle for different driving periods, complicated bifurcation diagrams of θ, responding to changes of parameter T are manifested. In Fig.
In this section, we consider the dynamics structure reconstruction of the experimental sets (Fig.
Since phase angle data 
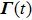
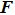

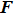
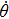
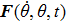
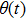
This task can be formally done as follows. By expanding 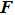
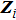
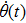
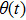
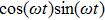
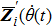
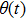
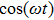
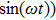
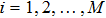
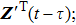
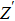
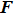
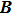
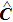
In Eq. (
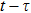
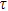
If all terms in
Since all elements of 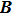
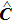
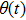
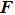
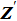
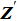
Up to now, there are still several points to be made clear before Eq. (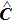
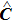
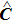
i) Since we are considering a pendulum system and measuring phase angle 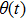
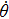
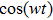

ii) In Eq. (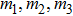
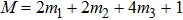
iii) After truncation M is fixed in Eq. (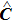
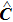

Considering all the above three items, a well-defined and closed algorithm Eqs. (
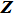

Using the data collected from the chaotic states at different Tʼs of Fig.
In order to justify the sufficiency of M truncation in Eq. (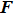

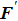


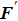
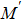
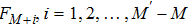
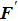
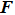
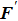

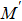
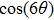
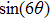
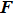
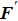

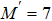
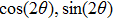
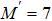
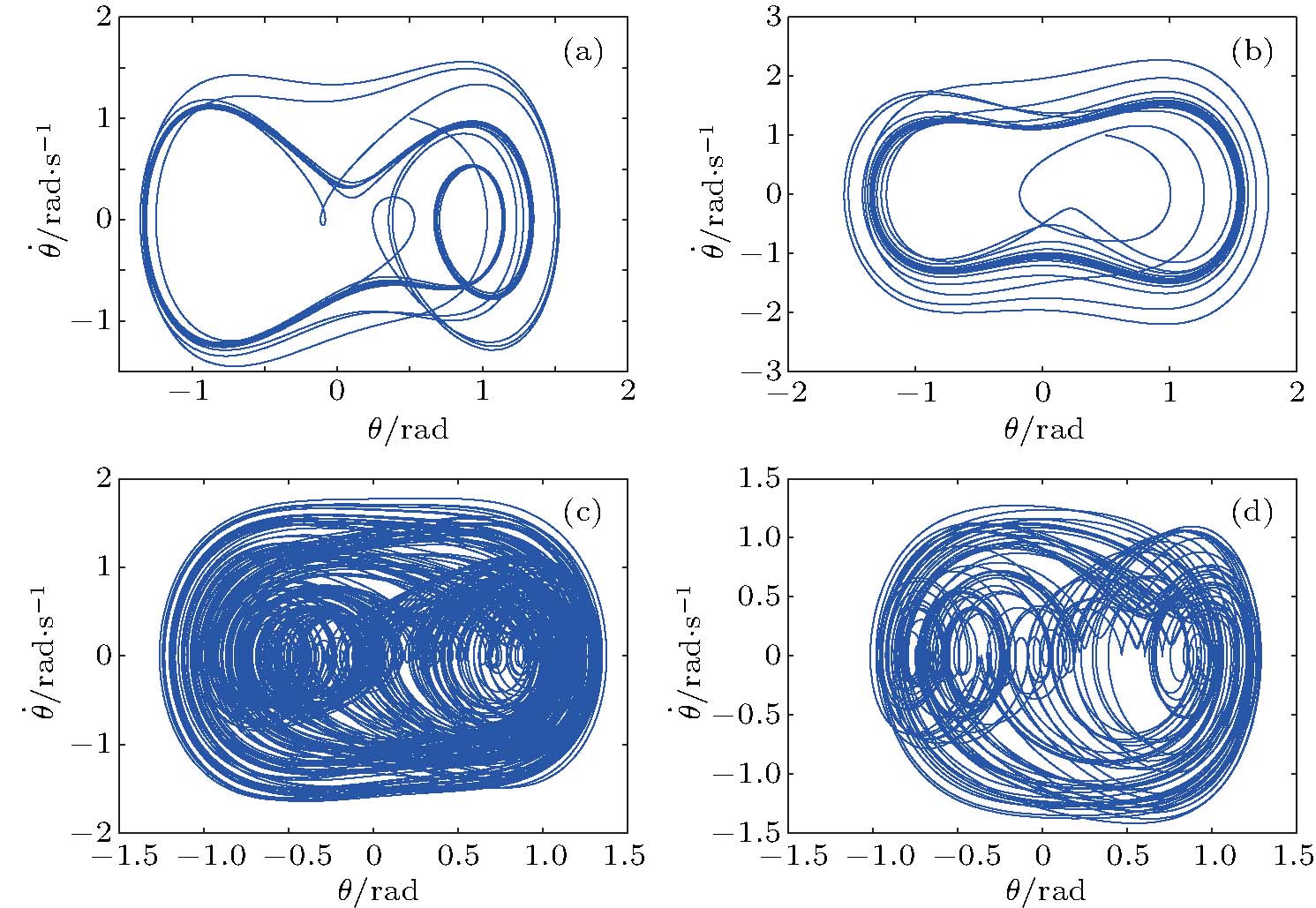
With parameters reconstructed by using Eqs. (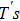
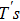
In Fig.
In conclusion, we have performed the dynamic structure reconstruction of an experimental set “Boer resonant instrument for forced vibration” based on measured experimental data only. So far, most of the works on the system reconstructions have considered various model systems. In this paper, the systematical analysis fully based on experimental data will be useful for practical applications in wide fields. In physics, we are familiar with various derivations, starting from physical first principles, i.e., a top-down investigation strategy. In this paper, we assume no prior knowledge of the experimental structure, except some general and well-known understanding of friction, driving and angle property of measured data. Purely from experimentally measured data, we can infer the structure of the experimental set. This bottom-up strategy can explore not only the “first principles”, i.e., the main dynamic structure, of the experiment, but also reveal the concrete parameter values in the experimental set, which cannot be directly derived from the first principles. In Figs.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] |