† Corresponding author. E-mail:
The electrical conductivities of single-crystal K-feldspar along three different crystallographic directions are investigated by the Solartron-1260 Impedance/Gain-phase analyzer at 873 K–1223 K and 1.0 GPa–3.0 GPa in a frequency range of 10−1 Hz–106 Hz. The measured electrical conductivity along the 


The explanation of geomagnetic deep sounding and magnetotelluric (MT) data from the deep interiors of earth’s and other planets’ deep interior relies on the known electrical properties of minerals and rocks established in the laboratory at the relevant temperatures and high pressures.[1–7] The MT field surveys have found zones of anomalously high conductivity (
Feldspar is a representative tectosilicate mineral characterized by a fundamental formula of MT4O8 (M denotes Na, Ca, K or Ba; T refers to Si or Al), and is the most abundant rock-forming alumosilicate mineral that contains 60% of the earth’s crust; it can be found widespread and commonly in various igneous, metamorphic, and some sedimentary rocks. In general, alkali (K+, Na+) or alkaline-earth (Ca2+, Ba2+) cations with large ionic radii occupy the M-sites in the feldspar crystal structure. The T-sites are occupied by a three-dimensional (3D) framework of different charges of tetrahedral Al3+ and Si4+ ions, which are widely used in the glass, ceramics, and cement industries. The composition and structural stability of feldspar make it an important component of the earth’s crust; its electrical properties at high temperatures and high pressures, combined with those of other typical rock-forming minerals in the deep crust (e.g., quartz, amphibole, clinopyroxene, orthopyroxene and mica) are crucial to establishing the conductivity–depth profile of the earth’s interior.[14–19]
The electrical conductivities of natural and synthetic alkali feldspar (both K-feldspar (KAlSi3O8) and albite (NaAlSi3O8), and their solid solution), anorthite (CaAl2Si2O8), and plagioclase have been extensively studied at high temperatures and high pressures.[20–34] It is important to know the electrical conductivity of K-feldspar, a crucial end member of feldspar, for explaining the conduction mechanism of K-feldspar-bearing rock deep in the earth’s crust. However, the several studies that have previously investigated this are limited in scope. Maury studies[23] reported the electrical conductivities of a series of polycrystalline feldspars at 673 K–1173 K and atmospheric pressure. Guseinov and Gargatsev[26] measured the electrical conductivities of natural pure microcline single-crystal feldspar and the maximum microcline single-crystal of feldspar with a minor albite phase at 373 K–1273 K and atmospheric pressure. Hu et al.[30] measured the electrical conductivities of hot-pressed synthetic polycrystalline dry K-feldspar aggregate at 1.0 GPa–3.0 GPa and 873 K–1173 K by using a multi-anvil press, and from the Nernst–Einstein equation they also calculated its diffusion coefficient. More recently, El Maanaoui et al.[34] investigated the anisotropic electrical conductivities of natural alkali feldspar from the German Eifel region with two distinct chemical compositions characterized by potassium to total-alkali cation ratios 


The present study reports the use of impedance spectroscopy to determine the electrical conductivities of single-crystal K-feldspar along three different crystallographic directions at frequencies of 0.1 Hz to 1 MHz. A series of characteristic parameters including the pre-exponential factor, activation energy, and activation volume are acquired. The single-crystal K-feldspar shows a large anisotropic electrical conductivity, and the results are compared with those of previous studies. At 2.0 GPa, the diffusion coefficient of ionic potassium is calculated by using the electrical conductivity data from the Nernst–Einstein equation. We also discuss in detail the conduction mechanism of the K-feldspar single crystal at high temperature (T) and pressure (P).
The natural K-feldspar megacryst in the present study was available from Pakistan. The surface of each sample was fresh, non-fractured, non-oxidized and purely gem-class single-crystal K-feldspar without any evidence of twinning, exsolution, alteration, secondary phase precipitation, structural flaws, or heterogeneity. Chemical compositions (see Table 




 | Fig. 1. (color online) Detailed description crystalline configuration, lattice plane and crystallographic axis for K-feldspar single crystal along three main directions. |
 | Fig. 2. Raman spectra of the starting material and the recovered sample: (a) the starting material used in this study, (b) the sample recovered from 3 GPa. All peaks are attributed to K-feldspar. |
| Table 1.
Chemical compositions of the starting material of K-feldspar. . |
K-feldspar samples were cut and polished into cylinders (diameter 6.0 mm, height 6.0 mm) using an ultrasonic drill and diamond saw. They were then cleaned sequentially with deionized distilled water, alcohol, and acetone, and baked for 48 h in a 473-K vacuum drying oven to remove any adsorbed water.
Vacuum Fourier transform infrared spectroscopy (FT-IR, Vertex-70V, Hyperion-1000 infrared microscope) at wavenumbers from 350 cm−1 to 8000 cm−1 was used to determine the water content values of doubly polished samples thinner than 


 |
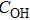

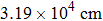

 | Fig. 3. Representative unpolarized FT-IR spectra of 
|
The water content values of K-feldspar before and after conductivity measurements were less than 
In-situ high-pressure electrical conductivity measurements of samples were performed using a YJ-3000t multi-anvil and a Solartron-1260 Impedance/Gain-phase analyzer (Schlumberger) in the Key Laboratory of High-Temperature and High-Pressure Study of the Earth’s Interior, Institute of Geochemistry, Chinese Academy of Sciences. Hui et al.[38] and Sun et al.[39] described in detail the measurement principles and experimental procedures.
The experimental setup for electrical conductivity measurements of feldspar at high pressure is illustrated in Fig.
 | Fig. 4. (color online) Experimental setup for electrical conductivity measurements of feldspar at high pressure. |
 | Fig. 5. (color online) Photomicrograph (plane-polarized reflected) taken with light from the recovered sample assembly after conductivity measurement. |
During the experiment, the pressure was raised to the designated value slowly at a rate of 1.0 GPa/h. At a constant pressure, the temperature was then increased gradually at 100 K/h to designated preset values in steps of 50 K. Impedance spectroscopy was measured on a Solartron-1260 Impedance/Gain-phase analyzer with a sinusoidal signal voltage of 1.0 V and a frequency range of 10−1 Hz–106 Hz. Four parameters of complex impedance including the real part (


 |
 |

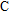
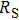

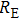
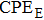

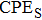

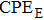
We measure the electrical conductivity of K-feldspar single crystals along the 


Figures 












The electrical conductivities of the samples (σ, S/m) are calculated by using the following equation:
 |
 |


 |
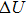
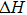
Figure
| Table 2.
Fitting parameters of Arrhenius relation of electrical conductivity along three crystallographic axes for K-feldspar single crystal at pressures of 1.0 GPa–3.0 GPa. The top five columns represent single crystals in the present study and the bottom three columns refer to the calculated isotropic average values of randomly oriented polycrystalline aggregates. The series, average, and parallel averaging schemes are employed to acquire the electrical conductivities of aggregate sample, i.e., |
The electrical conductivity of K-feldspar single crystal along the 



Figure 




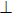



 |
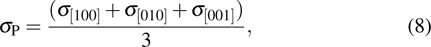 |
 |
These three isotropic average schemes transform the conductivity results along the three crystallographic axes into isotropic conductivity values for randomly oriented polycrystalline K-feldspar aggregates. The results from the series and parallel averaging represent respectively the minimum and maximum average conductivity. However, the present work shows that the magnitude of the anisotropic electrical conductivity of K-feldspar remains approximately constant across the whole temperature range (673 K–1223 K).
Figure 





 | Fig. 10. (color online) Anisotropic electrical conductivities of dry K-feldspar single crystal at 2.0 GPa in the present study compared with previous results. The lines are labeled as follows: black solid lines represent the results of this work; dark blue dashed and dotted lines represent electrical conductivities of the 




|
Figure
The logarithm of the electrical conductivity at each pressure and orientation varies linearly with the reciprocal of temperature, indicating that our samples have only a single dominant conduction mechanism. The activation volume (
 |
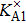
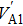



Electrical conductivity originates from the diffusion of a dominant charge-carrying species under a designated AC electric field. The correlation between electrical conductivity and isotope diffusion coefficient has been widely examined for many silicate minerals in order to link measured conductivities, the conduction mechanism, and diffusion data for charge carriers (e.g., ions, small polarons, protons etc.).[61–68] The K-feldspar studied here had only potassium ions at the interstitial sites verified to play an important role in bulk conductivity, and their diffusion coefficient can be obtained from the Nernst–Einstein equation:[69]
 |
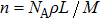

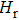


 | Fig. 11. (color online) Calculated diffusion coefficients of dry K-feldspar single crystal by using the Nernst–Einstein equation at 2.0 GPa, and their comparison with previous studies. Black solid lines represent the results of this work; pink dotted line represents the self-diffusion coefficient of sodium in natural single-crystal alkali sanidine with a chemical composition of 


|
Figure 





In light of this new result for the influence of crystallographic orientation on the diffusion coefficient of single-crystal K-feldspar, we compare five previous results obtained under different conditions. Lin and Yund[71] found the potassium self-diffusion coefficient for pure microcline perthite with a chemical composition of 



In summary, in the present study, strong anisotropies along the three main orientations in both the electrical conductivity and the potassium diffusion coefficient of K-feldspar are revealed by using the electrochemical impedance spectra at conditions of high temperature and high pressure, with anisotropic ratios (

We appreciate Dr. Aaron Stallard of Stallard Scientific Editing Company for polishing the English language of the manuscript.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] |