† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11672087, 11502058, and 11402252).
The phase diagram of HfO2–TiO2 system shows that when Ti content is less than 33.0 mol%, HfO2–TiO2 system is monoclinic; when Ti content increases from 33.0 mol% to 52.0 mol%, it is orthorhombic; when Ti content reaches more than 52.0 mol%, it presents rutile phase. So, we choose the three phases of HfO2–TiO2 alloys with different Ti content values. The electronic structures and optical properties of monoclinic, orthorhombic and rutile phases of HfO2–TiO2 alloys are obtained by the first-principles generalized gradient approximation (GGA)+U approach, and the effects of Ti content and crystal structure on the electronic structures and optical properties of HfO2–TiO2 alloys are investigated. By introducing the Coulomb interactions of 5d orbitals on Hf atom (



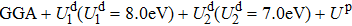
Among all candidate materials for the gate insulators of metal oxide semiconductor field effect transistors and the capacitor dielectrics of dynamic random access memories, HfO2 and TiO2 are promising candidates due to their properties.[1] The phase diagram, cell parameters and geometry structure for HfO2–TiO2 system have been studied. The main phase of HfO2–TiO2 is monoclinic (denoted as “m”), monoclinic + orthorhombic (denoted as “o”), orthorhombic, and orthorhombic + rutile (denoted as “r”), when TiO2 content values are less than 5%, 5%~33%, 33~52%, and 52~100%, respectively.[2–5] For example, HfTiO4 (i.e., Hf0.5Ti0.5O2) has a columbite-type (α-PbO2) structure with two formula units per unit cell, with orthorhombic symmetry, space group pb/cn, with the Hf and Ti atoms randomly distributed on the octahedral site of the α-PbO2 structure.[6,7]
The phase structure and optical properties of HfO2–TiO2 films are determined by preparation process and Ti content. Nanolaminate HfO2–TiO2 films are grown by reactive sputter deposition on unheated fused SiO2, sequentially annealed at 573 K to 973 K. A nanocrystalline structure of orthorhombic HfTiO4 adjacent to an interface followed by monoclinic HfxTi1 − xO2 was identified.[8] HfxTi1 − xO2 films on silicon substrates were prepared by the atomic layer deposition. As-deposited HfxTi1 − xO2 films remained amorphous after annealing up to about 1000 μC in N2 for 5 min.[1] Hafnium titanate films were deposited in a large Hf–Ti compositional range by atomic layer deposition. The o-HfTiO4 diffraction lines in the samples (30%–64% Hf) annealed at 850 μC have been observed. For an Hf content value higher than 82%, an m-HfO2-like structure was reported.[9] The x-ray diffraction of a 1:1 mixture of HfO2 and TiO2, prepared by the alkoxy hydrolysis technique and heating to ~750 μC, indicated that the material is mainly composed of 95% o-HfTiO.[4] The Ti addition stabilized the amorphous phase of HfO2. After high-temperature annealing, the films transformed from an amorphous into a polycrystalline phase. The o-Hf–Ti–O peaks were detected in polycrystalline films containing 33 mol% or higher Ti content. As Ti content decreased, m-HfO2 became the predominant microstructure.[10]
As far as we know, there is no paper studying electronic structure and optical properties of HfO2–TiO2 alloys by theoretical calculation based on density function theory, and there are very few studies on electronic structures and optical properties of HfO2–TiO2 alloys experimentally.[11] Thus, it is essential to investigate the electron structures of HfO2–TiO2 alloys with different phases and Ti content values and clarify the difference in optical property among different structures with variable Ti content from the first-principles calculations.
In this paper we use the GGA scheme and GGA + U scheme formulated by Loschen et al.[12] to calculate the lattice parameters, band structures and optical properties of m-, o- and r-HfTiO4 alloys. After introducing the on-side Coulomb interactions of 5d orbitals on Hf atom (




The first-principles calculations are performed with plane-wave ultrasoft pseudopotential by the GGA with Perdew–Burke–Ernzerhof (PBE) functional and GGA + U approach as implemented in the CASTEP code (Cambridge Sequential Total Energy Package).[15] The ionic cores are represented by ultrasoft pseudopotentials for Hf, Ti, and O atoms. For Hf atom, the configuration is [He]4f145d26s2, where the 5d2 and 6s2 electrons are explicitly treated as valence electrons. For Ti atom, the configuration is [Ar]3d24s2, where the 3s2, 3p6, 3d2, and 4s2 electrons are explicitly treated as valence electrons. For O atom, the configuration is [He]2s22p4, and 2s2 and 2p4 treated as valence electrons. The plane-wave cut-off energy is 380 eV, and the Brillouin-zone integration is performed over the 6 × 6 × 6 grid sizes by using the Monkhorst–Pack method for structure optimization. This set of parameters assures the total energy convergence of 5.0 × 10−6 eV/atom, the maximum force of 0.01 eV/Å, the maximum stress of 0.02 GPa and the maximum displacement of 5.0 × 10−4 Å.
In the following sections, we optimize the geometry structures of HfO2–TiO2 alloys by the GGA, and GGA





Finally, we calculate electronic structures and optical properties of m-Hf1 − xTixO2 (x = 0 mol%~50 mol%), o-Hf1 − xTixO2 (x = 12.5 mol%~87.5 mol%), and r-Hf1 − xTixO2 (x = 50 mol%~100 mol%), and study the effects of different phases and Ti content values on the electronic structures and optical properties of HfO2–TiO2 alloys. We analyze the change trend and give some reasonable explanations.
The space group of m-HfTiO4 alloy is p21/c and the local symmetry is C2h–5. Moreover, m-HfTiO4 alloy is fully characterized by lattice constants a, b, c, and β. In order to check the applicability and accuracy of the ultrasoft pseudopotential, the GGA calculation of the perfect bulk m-HfTiO4 alloy is carried out to determine an optimized a, b, c, and β. The resulting a = 0.507 nm, b = 0.5174 nm, c = 0.5337 nm, and β = 99.1° are in good agreement with the experimental value, a = 0.5078 nm, b = 0.5134 nm, c = 0.5271 nm, and β = 99.2°.[3]
From the band structure along high-symmetry points in the Brillouin zone, an indirect band gap is observed, and the band gap value Eg is about 2.66 eV by GGA. The resulting band gap of m-HfTiO4 alloy obtained by 

Figure
 | Fig. 1. (color online) (a) Imaginary part values of dielectric functions and (b) total density of state (DOS) in m-HfO2–TiO2 alloys with different Ti content values, obtained by GGA + U. |
From Fig.
The total DOS curves in the conduction bands shift leftwards. Namely, the position energies of the two shoulders decrease. It is easy to understand the reason why the ε2 value and total DOS in m- HfO2–TiO2 alloys vary. The total DOS in conduction bands near Fermi surface is mainly composed of Hf 5d state and Ti 3d state, where the first shoulder and the second shoulder correspond to Ti 3d state and Hf 5d state, respectively. It is well known that the energies of positions of Ti 3d state and Hf 5d state are about 3.0 eV[14] and 5.8 eV,[13] respectively, similar to the energies of positions of the two shoulders in total DOS of conduction bands near Fermi surface. The resulting denser available state (for Hf 5d state) in the conduction bands has wiped out the higher shoulder, while the thinner states (for Ti 3d state) have wiped out the lower shoulder in the imaginary part of dielectric function, respectively.
The space group of o-HfTiO4 alloy is pb/cn and the local symmetry is D2h-14. Moreover, o-HfTiO4 alloy is fully characterized by lattice constants a, b, and c. In order to check the applicability and accuracy of the ultrasoft pseudopotential, the GGA calculation of the perfect bulk o-HfTiO4 alloy is carried out to determine an optimized a, b, and c. The resulting a = 0.5073 nm, b = 0.5777 nm, and c = 0.5242 nm are in good agreement with the experimental values, a = 0.4756 nm, b = 0.5563 nm, and c = 0.5047 nm.[3]
From the band structure along the high-symmetry points in the Brillouin zone, an indirect band gap is observed, and the band gap value Eg is about 2.99 eV from the GGA. The resulting band gap of o-HfTiO4 alloy obtained by 
Figure
Figure
The total DOS curves in the conduct bands shift leftwards. Namely, the position energies of the two shoulders decrease, which is similar to those in m- HfO2–TiO2 alloys. The reason for variations of ε2 and total DOS in o-HfO2–TiO2 alloys is the same as that in m-HfO2–TiO2 alloys. By adopting these U values (


It is well known from crystal field theory[16] that the two peaks in the conduction bands are a result of the ligand field splitting of the Ti 3d and Hf 5d orbitals into two sets of t2g and eg states. The third shoulder in the Fig.
A comparison of our results about o-Hf0.875Ti0.125O2 alloy with the experimental results of imaginary part of dielectric function in the Hf0.88Ti0.12O2 film after annealing at high temperature in Ref. [10] is shown in Fig.
The space group of r-HfTiO4 alloy is p42/mnm and the local symmetry is D4h–14. Moreover, r-HfTiO4 alloy is fully characterized by lattice constants a and c. In order to check the applicability and accuracy of the ultrasoft pseudopotential, the GGA calculation of the perfect bulk r-HfTiO4 alloy is carried out to determine an optimized a and c. The results are a = 0.4856 nm and c = 0.3165 nm, there are no experimental values available to be compared with, and we give the experimental data of cell parameters of rutile TiO2, a = 0.4594 nm and c = 0.2959 nm.[17,18]
From the band structure along the high-symmetry points in the Brillouin zone, an indirect band gap is observed, and the band gap value Eg is 2.035 eV from the GGA. The resulting band gap of r-HfTiO4 alloy obtained by 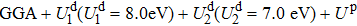
Figure
From Fig.
In Fig.
From the phase diagram of HfO2–TiO2 systems, we choose three phases of HfO2–TiO2 alloys with different Ti content values, i.e., monoclinic phase with a Ti content value of less than 50.0 mol%, orthorhombic phase with a Ti content value in a range from 12.5 mol% to 87.5 mol%, and rutile phase with Ti content value more than 50.0 mol%. The electronic structures and optical properties of monoclinic, orthorhombic, and rutile phase of HfO2–TiO2 alloys are obtained by the first-principles generalized gradient approximation (GGA) + U approach, and the effects of Ti content and phase on the electronic structure and optical properties of each of the HfO2–TiO2 alloys are discussed. By introducing the Coulomb interactions of 5d orbitals on Hf atom (




| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] |





