† Corresponding author. E-mail:
Projected supported by the National Natural Science Foundation of China (Grant Nos. 11675025, 11135007, and 11405012).
In this paper, we analytically explore the magnetic field and mass density evolutions obtained in particle-in-cell (PIC) and magnetohydrodynamics (MHD) simulations of a rarefied deuterium shell Z-pinch and compare those results, and also we study the effects of artificially increased Spitzer resistivity on the magnetic field evolution and Z-pinch dynamic process in the MHD simulation. There are significant differences between the profiles of mass density in the PIC and MHD simulations before 45 ns of the Z-pinch in this study. However, after the shock formation in the PIC simulation, the mass density profile is similar to that in the MHD simulation in the case of using multiplier 2 to modify the Spitzer resistivity. Compared with the magnetic field profiles of the PIC simulation of the shell, the magnetic field diffusion has still not been sufficiently revealed in the MHD simulation even though their convergence ratios become the same by using larger multipliers in the resistivity. The MHD simulation results suggest that the magnetic field diffusion is greatly enhanced by increasing the Spitzer resistivity used, which, however, causes the implosion characteristic to change from shock compression to weak shock, even shockless evolution, and expedites the expansion of the shell. Too large a multiplier is not suggested to be used to modify the resistivity in some Z-pinch applications, such as the Z-pinch driven inertial confinement fusion (ICF) in a dynamic hohlraum. Two-fluid or Hall MHD model, even the PIC/fluid hybrid simulation would be considered as a suitable physical model when there exist the plasma regions with very low density in the simulated domain.
The Z-pinch of wire-array (liner) has been considered as a promising drive approach to the ignition of inertial confinement fusion (ICF) and its fusion energy application due to its high conversion efficiency from electromagnetic energy stored to kinetic and radiation energy of implosion plasma.[1–6] While its plasma formation and implosion process are very complicated. There are a lot of measured images from the wire-array (without preconditioning) Z-pinch experiments to demonstrate that the majority of wire-array substance has been ablated due to Joule heating and is radially swept inward towards the array axis by
In most of simulations of wire-array Z-pinch, the ablation process of wire-array is ignored due to its complexity, and the wire-array is treated as a plasma shell with a precursor plasma inside, or the wires are treated as the metallic gas sources with high density and low temperature.[12,13] The metallic gas is partly ionized and expanded. The ionized gas is driven inward by Lorentz force, and a precursor plasma profile is formed. The density of ablated plasma inside the wire-array is varying all the way, and is possibly very low in the front of the precursor plasma, or the streams of the ablated plasma. For the very low plasma density it should be understood whether the currently used magnetohydrodynamics (MHD) model can accurately describe the magnetic field evolution and the electric fluid movement.
In the practice of Z-pinch simulation, which is mostly based on the radiation magnetohydrodynamics equations (model), for obtaining better simulation results, which agree well with the experimental data, such as convergence ratio, and x-ray power and energy, the electrical resistivity of Z-pinch plasma needs artificially modifing more or less.[12,14] The characteristic results might be obtained through this modification, but the magnetic field evolution and the pinch dynamic process might be changed unexpectedly. It is interesting and important to explore the variations of the magnetic field evolution and the dynamic process with this modification.
The discharged plasma is essentially a system consisting of a large number of charged particles, i.e., electrons and ionized ions. So the Z-pinch plasma can be treated as a huge charged particle system, and can be simulated through a particle-in-cell (PIC) code. In principle, it is to solve the Maxwell equations and particle motion equations.[15] Welch et al. first realized the fully kinetic particle-in-cell simulation of deuterium gas-puff Z-pinch on a Z machine.[16–18] They made use of the implicit, fully electromagnetic (EM) and kinetic particle-in-cell code LSP to simulate the Z-pinch process. Later Schmidt et al. extended the applications of LSP code to fully kinetic simulations of dense plasma focus devices, which were designed to produce fusion neutron resources.[19,20] Recently, the LSP code was used to simulate and assess the ion kinetic effects in a laser direct-drive capsule implosion experiment.[21] All these researches mainly focused on the neutron yields and production mechanism, rather than on the microscopic mechanisms of Z-pinch and focus.
Two years ago, we realized the particle-in-cell simulation of the rarefied deuterium shell Z-pinch in China.[22] In principle, the profiles and evolution of magnetic field obtained in the PIC simulation are believed to have higher reliability. Therefore, due to the lack of measured profiles of magnetic field during the Z-pinch process, they could be approximately considered as the real magnetic field in the Z-pinch plasma. So we can understand the validity of MHD simulation of the Z-pinch plasma under very low mass density through comparing their evolvements obtained in the MHD and PIC simulations. At the same time the comparison can help us to in depth understand the Z-pinch mechanism in physics.
It is a crucial matter for Z-pinch radiation MHD simulation that the magnetic field evolution and the radiation emission and transport are accurately modeled because the used physical models and parameters for the magnetic field and radiation may largely affect the simulated results. When the mass density of simulated plasma is very low, the produced radiation is quite weak and can be neglected in the simulation. So we can focus on the magnetohydrodynamic behavior of the rarefied deuterium shell Z-pinch.
In this paper, we show the statistical results of mass density evolution in the PIC simulation of the rarefied deuterium shell Z-pinch in Subsection
The rarefied deuterium plasma shell Z-pinch, which was simulated by a particle-in-cell code,[22] is now simulated by our 1D radiation MHD code.[12,23] At the beginning, the inner radius rin of the shell is 0.6 cm, the outer radius rout is 1.0 cm, and its height is 1.0 cm. The mass per unit length of the plasma shell is 1.0 × 10−12 g/cm, and the matched current is taken as I(t) = 433 sin4(πt/2T0) A, where t is the time and T0 is the rising time of the current (I) from 0 to peak. Here T0 is assumed to be 50 ns. The mass density of the shell is about 4.97 × 10−13 g/cm3. The emission of radiation would be very weak during the shell Z-pinch due to very low plasma density, and the radiation effect on the shell Z-pinch dynamic process would not be considered in its MHD simulation. The free path of particle collision is still substantially smaller than the size of the shell, and the fluid description may be suitable for its magnetohydrodynamic process. Therefore, we simulate the Z-pinch process of the rarefied deuterium plasma shell by the 1D MHD code. Generally, the Spitzer resistivity (η = 5.2 × 10−3zlnΛ/T3/2 Ω⋅cm, where z is the ionization degree, lnΛ is the Coulomb logarithm, and T is the plasma temperature in units of eV) is adopted in solving the magnetic field equation. The resistivity is sometimes modified by being multiplied by a factor for obtaining better results. When a multiplier of 2 is applied to the Spitzer resistivity, which approximately means that the resistivity perpendicular to the azimuthal magnetic field is adopted in the simulation.
Figure
In the Lagrangian MHD simulation, we can record the flow lines of the simulated mass points. Figure
Figure
 | Fig. 3. (color online) Profiles of mass density at 5 ns, 25 ns, 35 ns, 40 ns, 45 ns, 50 ns, and 55 ns, calculated in MHD simulations with the used multipliers of (a) 2 and (b) 1000. |
In Z-pinch MHD simulation it is well known that the simulated Z-pinch process is sensitive to the modification of plasma resistivity. Compared with the macroscopic experimental data, the good simulated results could be obtained through the resistivity modification, but the dynamic process presented in the simulation might be changed a lot, even deviated from the reasonable one. Now we begin to explore how the modified resistivity affects the magnetic field evolution and the dynamic process of Z-pinch in the MHD simulation.
Figure
 | Fig. 4. (color online) Variations of magnetic field profile with the used multiplier in the MHD simulation at 25 ns (a), 35 ns (b), 45 ns (c), and 55 ns (d). |
Figure
 | Fig. 5. (color online) Radius variations of outer and inner interfaces (a), and mass center (b) of the shell with time under a few multipliers applied to Spitzer resistivity in the MHD simulation. |
Figure
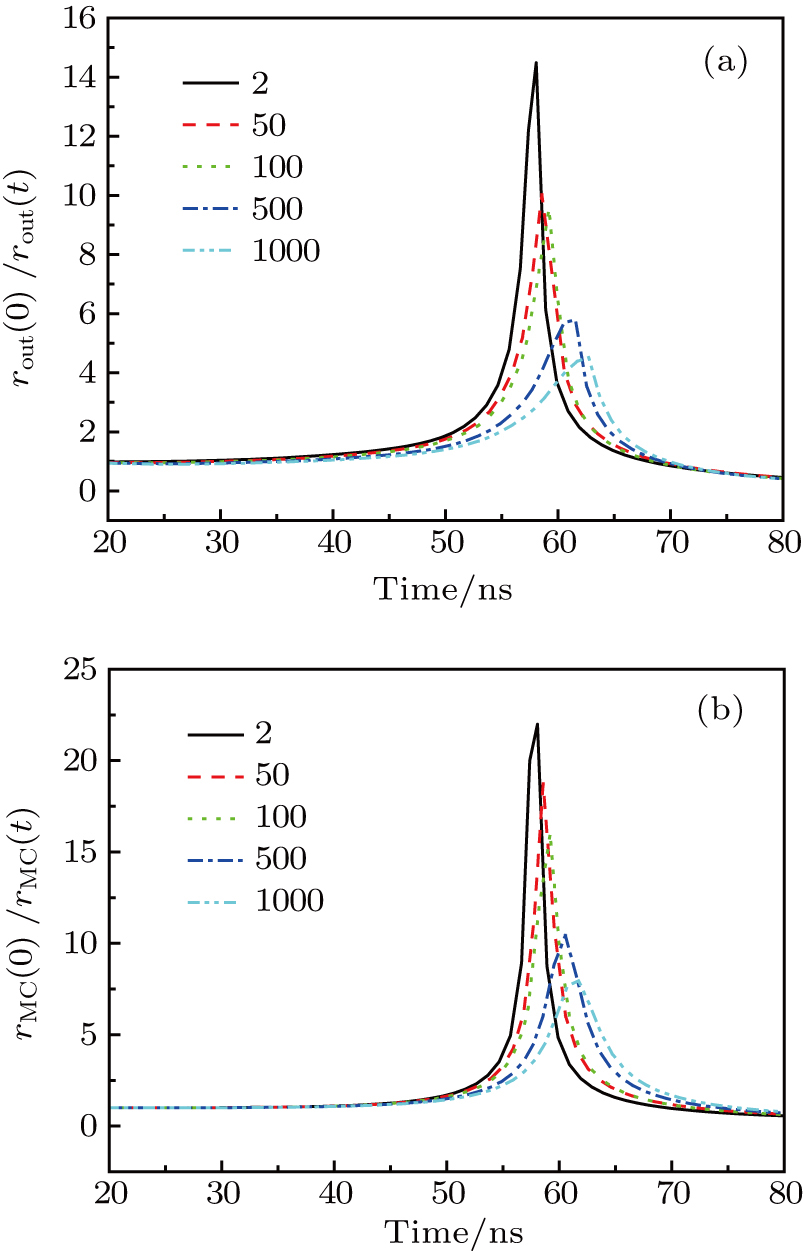 | Fig. 6. (color online) Variations of convergence ratio of outer interface (a) and mass center (b) of the shell with time under a few multipliers used in the MHD simulations. |
Figure
 | Fig. 7. (color online) Variations of mass density profiles with the used multiplier in the MHD simulation at 25 ns (a), 35 ns (b), 45 ns (c), and 55 ns (d). |
Figure
In the PIC simulation, a few millions of simulated particles are tracked, and the integrated evolution of the particle positions reveals the dynamic process of the shell Z-pinch.[22] For comparing the Z-pinch characteristics obtained by the MHD simulation with that by the PIC simulation, their mass center implosion trajectories are calculated. They are defined as rc = ∫ρr2\dr/∫ρr\dr in the MHD simulation, and

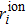
The magnetic field distribution and evolution are governed by the induction equation of magnetic field, which just includes the convection and diffusion terms due to adopting the Ohm’s law
Here we compare the magnetic field profiles calculated by the MHD and PIC simulations at different times. Firstly Figure
When the used Spitzed resistivity is enlarged, the magnetic field diffusion will be enhanced and the convergence ratio becomes close to that obtained in the PIC simulation. Will their magnetic field profiles and evolutions become the same? Figure
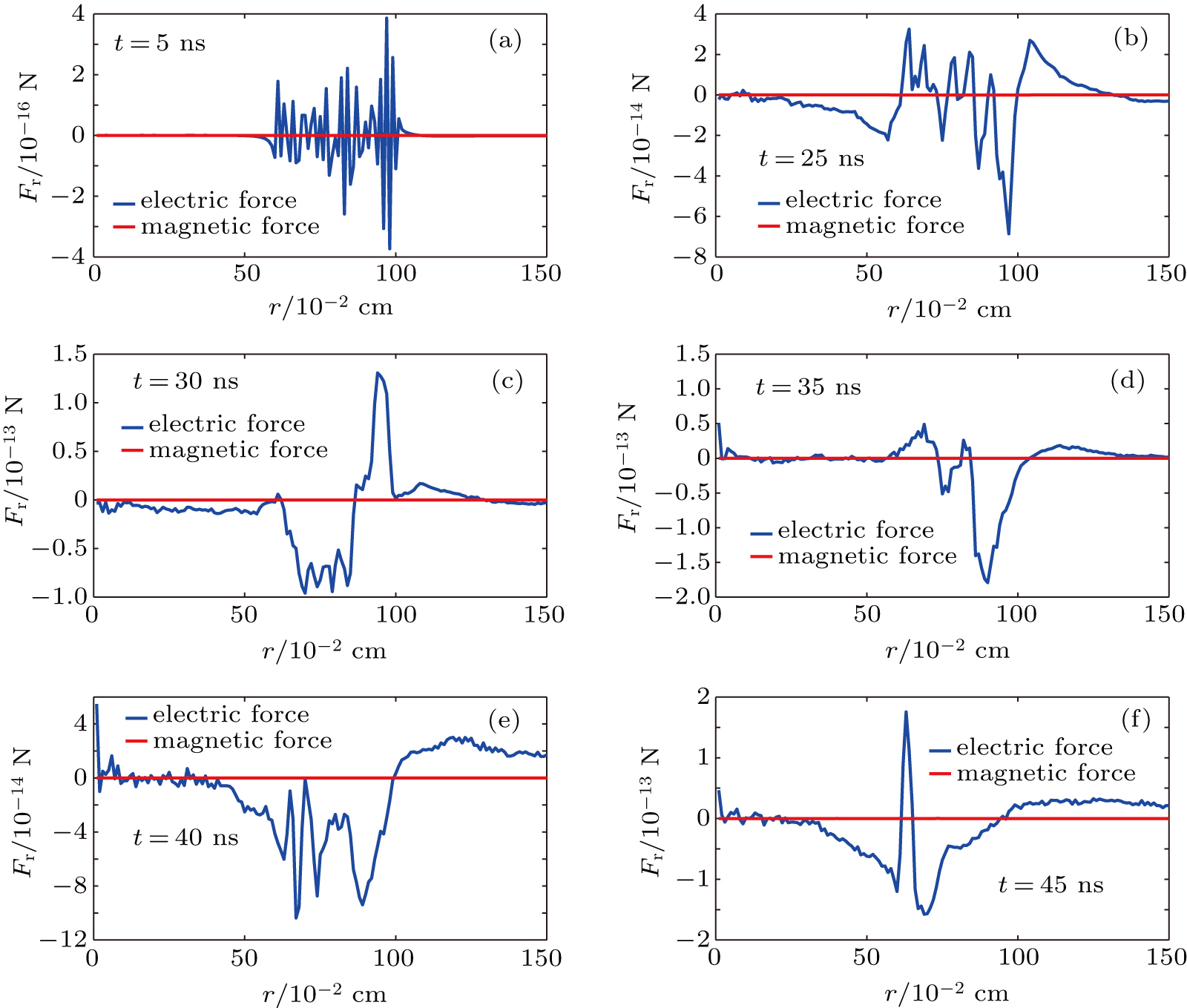
In the MHD simulation of Z-pinch, the whole plasma shell is driven inwards by Lorentz force
In the radial direction the electric and magnetic forces exerted on the electrons are comparable in magnitude,[22] while the forces exerted on the ions are mainly the electric forces. So, in the Z-pinch process the electrons should be first accelerated in axial electrical field and reach higher velocities, then they are driven inwards to the axis at the same time by the radial magnetic forces (i.e., Lorentz forces −qυzBθ, where q and υz are the charge and the axial velocity of electron, respectively, and Bθ is the azimuthal magnetic field), which causes the separations between the electrons and ions because the ion mass is much larger than the electron’s, and in turn a strong electrostatic field is produced. The produced electrostatic field attracts the ions to move towards the electrons. That is to say, the Z-pinch mechanisms are different under the descriptions of single fluid MHD and particle kinetics.
We cheerfully note that the mass density evolutions obtained in the PIC and MHD simulations are similar in the phase of shock wave compression after 45 ns (see Figs.
However, compared with the magnetic field profile obtained in the PIC simulation, the diffusion of the magnetic field seems to be underestimated in the MHD simulation. Even though their convergence ratios become almost the same, the magnetic field in the PIC simulation distributed inside the shell is higher than that in the MHD simulation mostly. Theoretical analysis demonstrates that the ion inertial length (c/2πfpi, where fpi is the ion plasma frequency) is comparable to the size of the shell with very low density considered in this paper. In this case, the magnetic field becomes mainly frozen into the electron fluid rather than the bulk plasma, and the two-fluid or Hall MHD model, even the PIC/fluid hybrid simulation would be used.[25–30] Therefore, in the wire-array Z-pinch (single-fluid) MHD simulation in which the processes of wire ablation and plasma expansion are considered, the plasma density needs to be truncated when it is too low.
When a radiation research of Z-pinch is located outside the Z-pinch plasma, such as the researches of radiation effect on material and the measurement of plasma opacity, the Z-pinch dynamic process will be relatively isolated from the interaction process of radiation and material. The requirement for the accurate simulation of Z-pinch plasma might be relaxed to some extent, and a larger multiplier could possibly be used in resistivity modification to obtain a more reasonable x-ray radiation pulse waveform. While in the scheme of dynamic hohlraum for Z-pinch driven ICF the ablated implosion process of a capsule embedded in the dynamic hohlraum is tightly connected with the wire-array (liner) implosion process. The action process of the capsule depends on the implosion process of the plasmas outside the capsule. In this case, if a larger multiplier (say, several tens or hundreds) is used, the inner part or shell of the plasma profile will be driven to implode earlier due to the artificially enhanced magnetic diffusion, and in turn it will unexpectedly cause the capsule action earlier.
We should point out that the required multiplier to modify the resistivity nominally for more reasonable result of Z-pinch simulation would decline with the increase of atomic number due to the possibly high ionization degree for a certain current level. In this paper the largest multiplier 1000 is used to restrain the convergence ratio to a value close to the convergence ratio of the PIC simulation because the atomic number of deuterium is the smallest in all the elements.
The Z-pinch processes of the rarefied deuterium current-carrying shell are simulated by the MHD and PIC codes, respectively. Their results, especially the magnetic field and mass density profiles and evolutions, are analytically compared with each other. In the MHD simulation the variation trends of the implosion characteristic and mass density, magnetic field, convergence ratio and temperatures with the increasing resistivity are explored in detail. Firstly, compared with the magnetic field profiles obtained in the PIC simulation, the magnetic field diffusion cannot be adequately revealed in the MHD simulation under the very low plasma density, though the fluid dynamic behaviour is still qualitatively described. For accurately simulating the whole wire-array Z-pinch process, two-fluid or Hall MHD model, even the PIC/fluid hybrid simulation would be possibly required. Secondly, there is a significant difference in the evolution of mass density profile between the PIC and MHD simulations before 45 ns (during the snowplow like implosion phase) of the shell Z-pinch because of the different pictures of forces exerted on ions and fluid. After the shock formation in the PIC simulation, the mass density evolution is similar to that in the MHD simulation for the case of using multiplier 2 to some extent. Thirdly, the MHD simulation results suggest that the magnetic field diffusion is enhanced greatly by increasing the Spitzer resistivity used. In turn it causes the implosion characteristics to change from the shock compression to weak shock, even shockless evolution, and cause the shell to expand more obviously, thereby slowing down the implosion process and reducing the convergence ratio. The peak temperature of electron increases and then reaches a saturate value, while the peak temperature of ion declines with the increasing of resistivity used. Finally, in the MHD simulation, though the nominally better simulation results could be obtained by modifying the used resistivity, too large a multiplier is not suggested to be used in the Z-pinch in which the applied sample (object) is tightly coupled with the imploding plasma, such as the Z-pinch driven ICF in a dynamic hohlraum. If too large a multiplier is applied, it may induce the earlier inward movements of the inner plasma, and may generally result in an unreasonable implosion picture.
The particle-in-cell simulation of Z-pinch makes us understand in depth the microscopic kinetic process and the applicability of MHD simulation in very low plasma density. Practically, (radiation) MHD simulation is still the main numerical program tool in the physical understanding, experimental designs and data analysis of Z-pinch. In the future, the PIC simulation should be continuously developed and applied for the microscopic investigation of Z-pinch with higher mass density, and the physical models used in MHD simulation should be developed hand-running for the magnetic field evolution calculated accurately during the Z-pinch.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] |