† Corresponding author. E-mail:
Entanglement between particles is a crucial resource in quantum information processing, an important example of which is the exploitation of entangled photons in quantum communication protocols. Among the different available sources of entangled photons, semiconductor quantum dots (QDs) excel owing to their deterministic emission properties, potential for electrical injections, and direct compatibility with semiconductor manufacturing techniques. Despite the great promises, QD-based sources are far from being ideal. In particular, such sources present several critical issues, which require the overcoming of challenges pertaining to spectral tunability, entanglement fidelity, photon indistinguishability and brightness. In this article, we will discuss the potential solutions to these problems and review the recent progress in the field.
In 1935, Einstein, Podolsky, and Rosen presented a thought experiment to describe the peculiarity of the quantum entanglement.[1] In a many-body entanglement system, the quantum state of each constituting particle cannot be described independently, even when the particles are separated by large distances. The exploitation of the entanglement in quantum information processing (QIP), e.g., quantum computing,[2,3] quantum cryptography,[4,5] and quantum teleportation,[6,7] has attracted significant attentions in the last decade. In this regard, it is crucial to develop high-quality sources for entangled quantum bits (qubits). At present, the generation of entangled qubits has been realized in various systems, such as atomic ions,[8,9] superconductor circuits,[10] electrons,[11,12] diamonds,[13] and photons.[14,15] In this article, we focus on the recent developments of polarization-entangled photons generated by semiconductor quantum dots (QDs).
In analogy to the classical information science, which uses the binary bits 0 and 1 to store information, the basic entity of quantum information is the qubit. The basic states to form an orthogonal basis of the qubit space are called computational bases. Considering a two-state system, for example, if the computational bases are 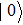
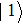
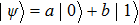

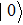
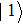
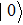
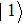

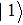
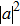
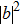
 | Fig. 1. (color online) Common physical realizations of qubits.[16] |
The photon, whose modern concept was developed by Albert Einstein, is a fundamental particle exhibiting the wave-particle duality. In other words, photons are self-oscillating short electromagnetic waves and particles with spin 1 at the same time. Photons can be used as flying qubits in QIP, due to their unique properties mentioned above. In particular, a single photon possesses many degrees of freedom (e.g., spin angular momentum, orbital angular momentum, arrival time, frequency, and so on), which can be used to encode a coherent superposition of states. Figure
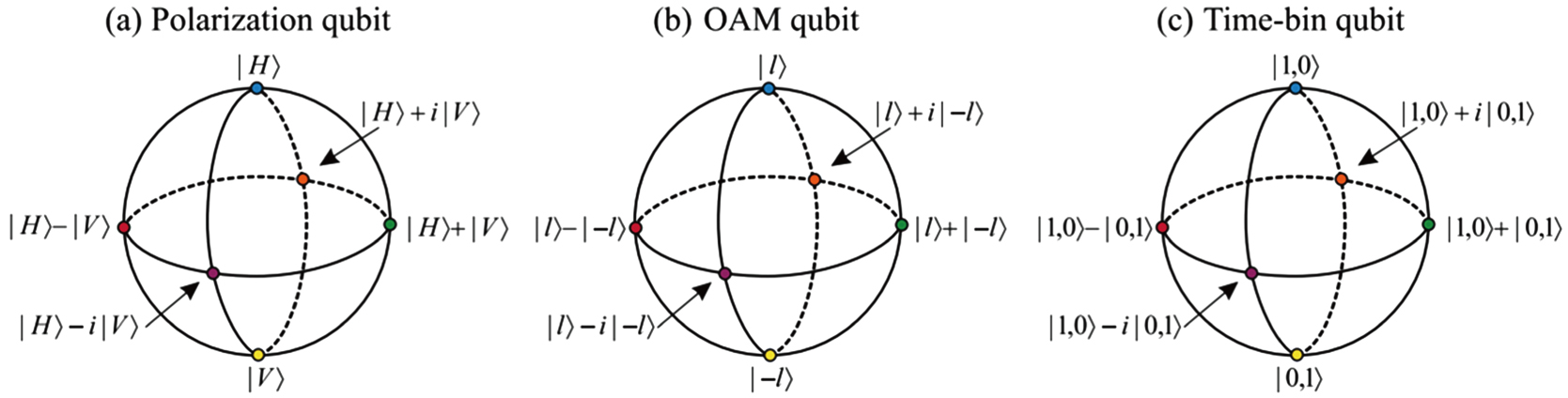 | Fig. 2. (color online) Bloch sphere representations of (a) polarization qubit, (b) orbital angular momentum qubit, and (c) time-bin qubit.[17] |
If we describe the photon as an electromagnetic wave, its polarization represents the oscillation direction of the electric field. In this viewpoint, the circular polarization is the spin angular momentum of the photon, with the left-handed and right-handed circular polarizations corresponding to +h and −h spin state, respectively. As shown in Fig. 
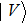
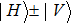
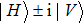
The orbital angular momentum (OAM) of photons, which represents the spatial distribution of the electromagnetic field, is associated with the helical or twisted phase front. The schematic is shown in Fig.
 | Fig. 3. (color online) Helical phase fronts of OAMs with different indexes.[18] |
The time-bin encoding is based on the arrival time of a single photon. A detailed experimental configuration was firstly proposed by Brendel.[23] A photon is sent into a two-path setup, then the quantum state of the photon can be described by 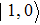

The quantum entanglement describes a nonlocal property of quantum correlations between multiple systems. It can be described mathematically in an elegant way. Here, we refer to a two-body system for example. Let us consider two physical subsystems A and B, whose respective Hilbert spaces are 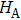


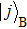
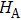

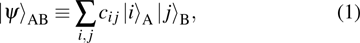 |
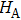

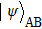
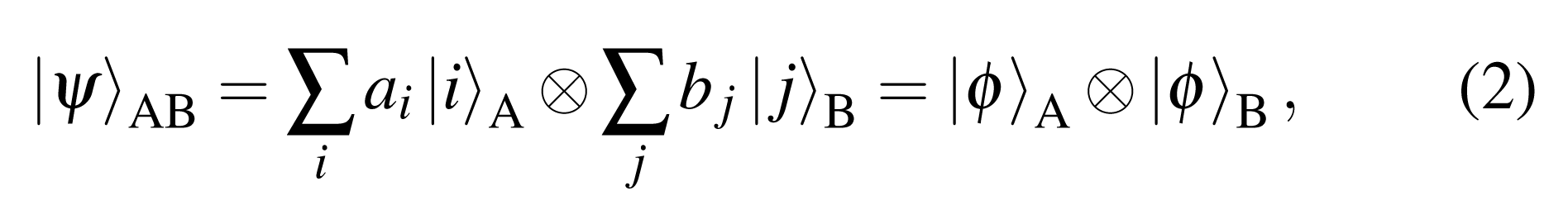 |
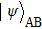
In the following we mainly focus on polarization-entangled photon pairs. The electric vector of an electromagnetic wave can be described by any orthogonal polarization basis, such as horizontal 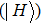
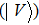
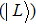
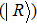
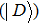
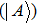
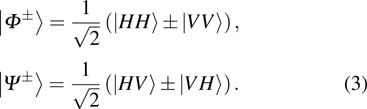 |
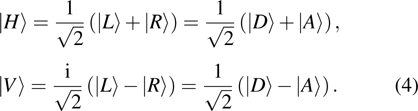 |
In the early years, polarization-entangled photon pairs were generated from the cascade radiations of single calcium (Ca) atoms.[25,26] The schematic diagram is shown in the following Fig.
 | Fig. 4. (color online) Two photons cascade radiation in a Ca atom.[27] |
By using the two-photon pumping technique, one electron is excited from the ground energy level 4s2 


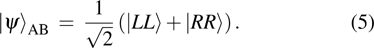 |
Spontaneous parametric down-conversion (SPDC), which was observed in the 1960s, describes a nonlinear optical effect in crystals, such as beta-barium borate (BBO) and potassium dihydrogen phosphate (KDP). More specifically, when a pump light is irradiated on a nonlinear crystal, a small portion of photons will interact with the crystal itself to generate down converted photons. In this process, the pump photon will generate a signal photon and an idler photon, and the three photons must fulfill the energy and momentum conservations, as well as the phase matching condition. Signal and idler photons are entangled in their polarizations. As shown in Fig.
 | Fig. 5. (color online) Type-I (a) and Type-II (b) spontaneous parametric down-conversion.[27] |
In type-I SPDC, the two output photons have the same polarization direction, whereas in type-II SPDC, the two output photons have polarization directions perpendicular to each other. The corresponding entangled states are also shown in Fig.
The III–V group semiconductor QDs, particularly QDs based on indium arsenide (InAs) and gallium arsenide (GaAs), possess the type-I energy-band alignment and can efficiently confine both electrons and holes in nanometer dimensions. As a result, the exciton effect is dominating in emission. When the QDs are symmetric enough, they can be the leading candidates for a deterministic generation of polarization-entangled photons. We will discuss the influence of symmetry on entanglement properties of QDs’ emission later, for the moment we only consider the QDs having a 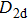
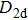
 |
In 1964, John Stewart Bell proposed a mathematic formulation (the famous Bell inequality) to test the local hidden variable theories. Five years later, John Clauser, Michael Horne, Abner Shimony, and Richard Holt generalized the Bell inequality to CHSH inequality, and proposed a practical experiment to test the EPR paradox. Since then, many endeavors have been made to realize loophole-free Bell inequality tests.[25,31–37] According to the Bell theorem, the key points to verify the entanglement of two particles are the simultaneous measure of the physical properties of the two particles and the analysis of their correlations. The Hanbury Brown and Twiss (HBT) setup is usually employed in these types of experiments, as shown in Fig.
 | Fig. 7. Two-channel photon correlation detection setup.[38] QWP and HWP denote quarter wave plate and half wave plate, respectively. |
The black box stands for a source of generation of photon pairs. In the experiment, the generated two photons are separated into two different channels by a non-polarizing beam splitter. The quarter wave plate, half wave plate, and polarizer are used to project the photon onto different polarization bases in each channel. The avalanche photodetector and time-correlated single-photon counting system are used to analyze the correlations between the two photons.
After obtaining the correlation data, there are two methods to test the degree of polarization entanglement of the two-photon state. The first method consists in the direct examination of the CHSH inequality, whereas the second one is the quantum state tomography. The CHSH inequality can be written as[27,39]
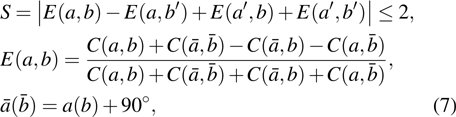 |
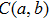

Another way to evaluate the entanglement is to reconstruct the density matrix of the studied quantum system. For a two-photon AB system, the polarization state 
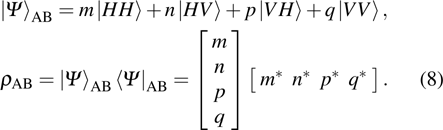 |
 |

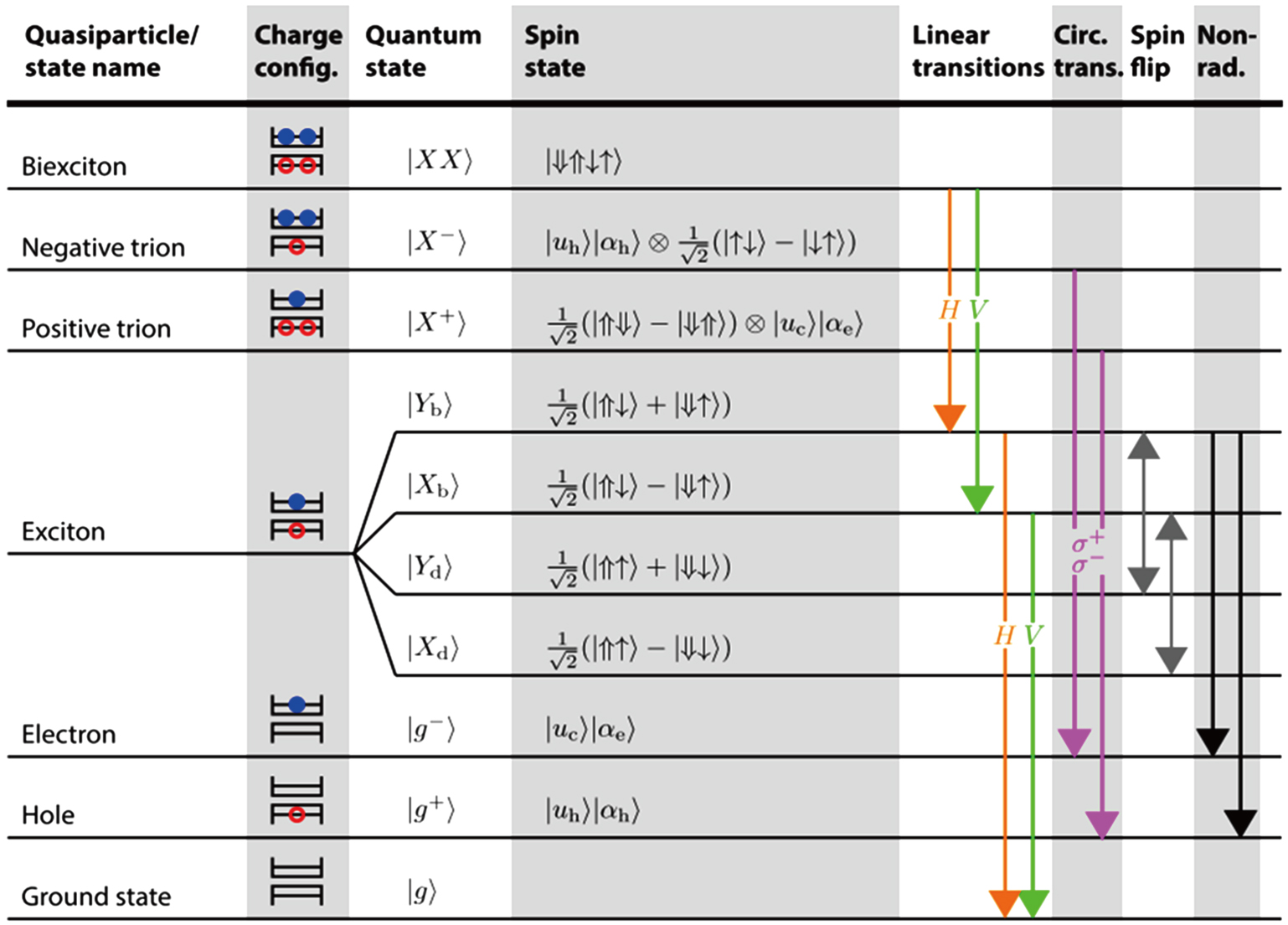 | Fig. 8. (color online) Group of basic exciton states in semiconductor QDs.[41] The double and single arrows in Dirac kets indicate the spin directions of holes and electrons, respectively. X, XX, and g denote exciton, biexciton, and ground states, respectively. The subscripts b and d denote bright and dark excitons, respectively. |
In addition to the quantum tomography, the entanglement fidelity is often used as an easily determinable quantity to characterize the degree of an entanglement. In general, the fidelity represents the closeness of one state to another. For example, the entanglement fidelity of a two-photon polarization state to 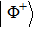
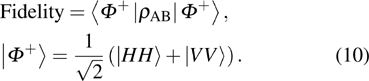 |
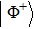
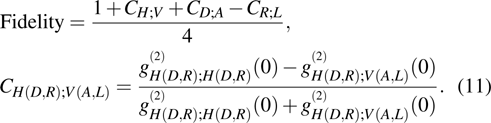 |
Semiconductor QDs are zero-dimensional nanostructures, and their optical and electrical properties can be artificially tailored by shape, size and compositions. Due to the strong quantum confinement, excitons-related effects are dominating in QDs. Such feature makes semiconductor QDs eligible for application opportunities in quantum optics.
The various exciton states in a single III–V group semiconductor QD are shown in Fig.
As far as the III–V group semiconductor QDs concern, here we mainly focus on the InAs- and GaAs-based ones. In this context, the anisotropy of strain, composition and shape reduces the symmetry of QDs to C2v or even lower C1. Considering the exchange interaction, there will be an energetic splitting between the two bright excitons, which is called fine-structure splitting (FSS), as shown in Fig.
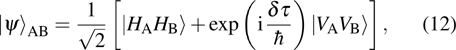 |
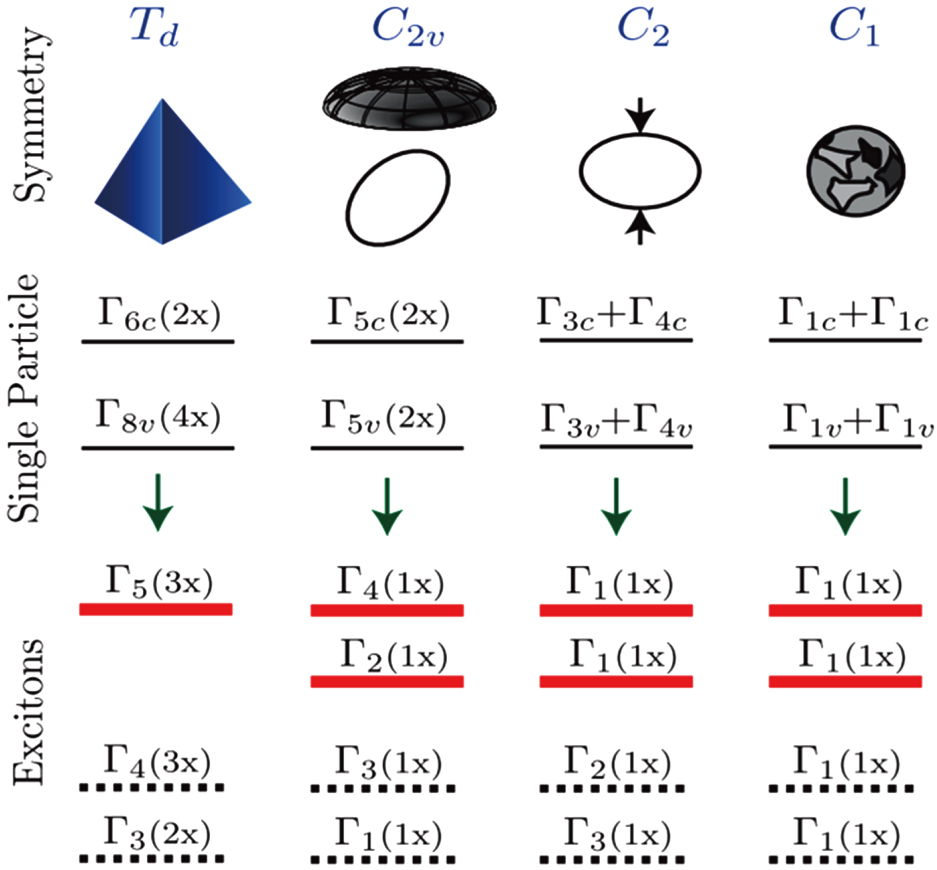 | Fig. 9. (color online) Symmetry analysis for four different point groups. The single-particle levels for the highest occupied and lowest unoccupied states are indicated by solid black lines. The ensuing irreducible representation of bright and dark excitons are indicated by thick red and dashed black lines, respectively.[46] |
More systematically, by constructing an effective two-band model based on the two bright excitons, Gong et al. claimed that the lower bound of FSS under uniaxial stress can be predicted by the polarization angle, and that both the FSS under zero stress and the critical stress can be determined by monitoring the changes in the polarization angle of the exciton.[47] The FSS is related to the uniaxial stress according to a parabolic function; therefore, it is possible that the FSS cannot go down to zero under a mere uniaxial stress. This provides a feasible method to select QDs for entangled-photon sources.
Because semiconductor QDs are used as entangled-photon sources, the community has made great efforts to eliminate FSS. An ideal quantum light source, which can be excited either optically or electrically, should possess good properties of brightness, entanglement fidelity, indistinguishability, coherence and on-demand (tunable wavelength and repetition frequency) at the same time. For semiconductor QD-based polarization-entangled photon sources (PEPS), there are three main tasks to be carried out: the manipulation of FSS; the optimization of the excitation condition; and the rational design of optical structures. In recent years, we have witnessed great success in this field.
The FSS mainly originates from the structure asymmetry; therefore its manipulation via the growth control of QDs is straightforward. However, typical InAs QDs grown on GaAs (001) crystal plane using the Stranski–Krastanow method suffer from strain and alloy intermixing, as well as shape elongation.[48,49] Hence, the symmetry of this type of QDs is lower than C2v. In 2009, two theoretical articles[50,51] predicted that InAs QDs on GaAs (111) crystal plane would have a symmetry higher than C3v, hence a small FSS. The results of the calculation of the wave function symmetry are shown in Figs.
 | Fig. 10. (color online) (a) and (b) Orientation of electron (blue) and hole (yellow) wave functions for a lens-shaped QD on two substrates with different orientations.[50] (c) Atomic force microscope analysis of the sample surface in the work by Kuroda et al.[54] (d) Scheme of the pyramidal QD structure.[52] (e) Profile of the pyramidal InGaAs1−xNx QDs (the upper figure is the atomic force microscope results, the lower figure shows the SEM result of the sample after removing the substrate).[53] |
GaAs/aluminum gallium arsenide (AlGaAs) QDs are an interesting alternative to the conventional InAs/GaAs QDs.[49,55] In 2013, Kuroda et al. used a droplet epitaxy method to realize self-assembled GaAs QDs on (111)A substrates[54] (see Fig.
Another emerging possibility to obtain highly-symmetric growths of GaAs/AlGaAs QDs is to use the droplet etching and nanohole etching techniques.[57–60] Recently, Huber et al. reported that, with preselected QDs in the sample, emissions of entangled photons can be obtained with high single-photon purity, high indistinguishability and high entanglement fidelity (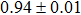

 | Fig. 11. (color online) (a) Droplet etching and nanohole infilling technique for the GaAs QDs growth. (b) Comparison of FSS between two kinds of QDs. (c) Entanglement fidelity as a function of FSS.[62] |
Post-growth tuning knobs, for example, the electric field,[63–67] magnetic field,[68–70] strain field,[47,71–85] thermal annealing,[86–89] and their combinations, can effectively manipulate the FSS of QDs. For practical applications of QD-based sources, these techniques are indispensable.
The first breakthrough in electric field-controlled PEPS based on InAs QDs was reported by Bennett et al. in 2010.[67] As shown in Fig. 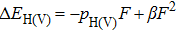
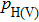
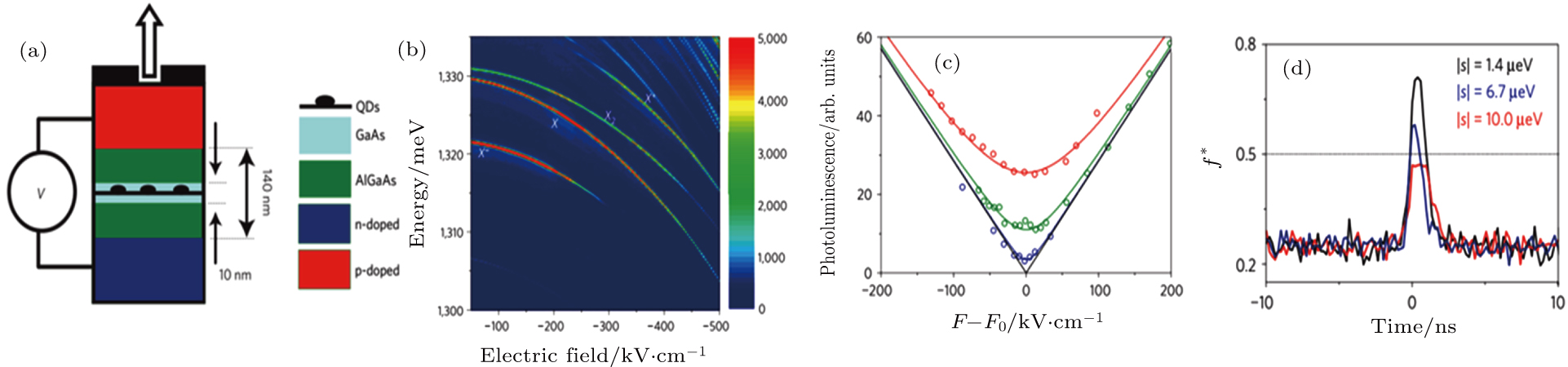 | Fig. 12. (color online) (a) and (b) Device design and observed giant Stark shift of the excitonic transitions. (c) FSS of three QDs controlled by vertical electric field. (d) Entanglement fidelity of three QDs with different FSS.[67] |
A similar work based on GaAs QDs was reported by Ghali et al.[63] An n–i–Schottky diode was used to realize the electric field tuning of the QDs’ FSS. The device structure and energy band profile along the growth direction are shown in Fig.
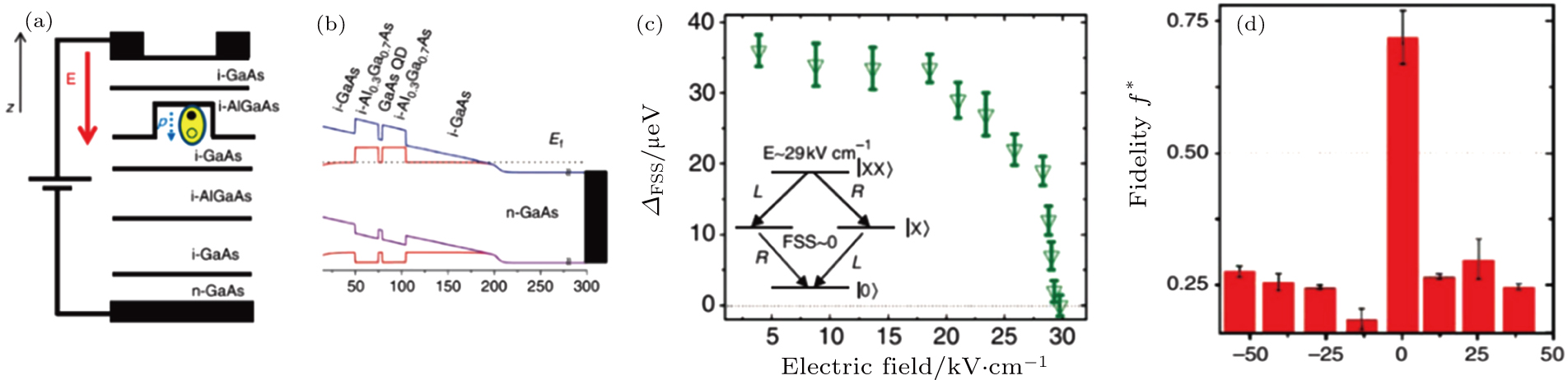 | Fig. 13. (color online) (a) Schottky-type device containing QDs. The polarization of QD exciton dipole moment is indicated by the dotted arrow. (b) z-direction energy band diagram. (c) Nonlinear dependence of FSS on external electric field. (d) Results of the entanglement fidelity.[63] |
Another interesting result was reported by Muller et al.[90] A continuous-wave laser was used to tune the QDs in the alternating current Stark limit to eliminate the FSS. It was observed that FSS decreases as the intensity of the tuning laser increases.
The effect of magnetic fields on QDs’ FSS was studied in detail by Bayer et al.[70] The first PEPS based on magnetic field tuning was reported by Stevenson et al. in 2006.[68] Four years later, they reported that the in-plane magnetic field can be used to tune the FSS more effectively, with a tuning coefficient of up to 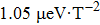
The electrical field tuning may introduce excessive carriers around the quantum dots and degrade the coherence of the emitting photons. Furthermore, large electrical fields can lead to quenching effects. Nevertheless, the magnetic field tuning is not suitable for practical applications due to the bulky setup. An emerging technique consists in the usage of strain fields. The early studies in this context were reported by Seidl et al.[92] and Ding et al.[71] In particular, they used piezoelectric lead zirconic titanate (PZT) and [Pb(Mg1/3Nb2/3)O3]0.72[PbTiO3]0.28(PMN-PT), respectively, to tune the exciton states of the self-assembled QDs. In the latter work, thin membranes containing QDs were used to significantly increase the strain tuning range. Plumhof et al. reported the influences of anisotropic strain fields on the FSS of InAs and GaAs QDs, for the first time.[72] Trotta et al. realized the simultaneous application of large strain and electric fields, leading to the successful elimination of FSS for almost each QDs in the sample.[75] In 2012, a strain-tunable quantum light-emitting diode (QLED) was also reported.[74]
The first experimental demonstration of strain-tunable QLED emitting polarization-entangled photon pairs (also called ELED) was realized by Zhang et al.[79] As shown in Fig.
 | Fig. 14. (color online) (a) Sketch of the diode structure. The PMN-PT was cut in a way that it can exert large anisotropic strain fields on the bonded ELED. (b) Entanglement fidelity as a function of FSS. (c) Representative variation of FSS of the high-energy component of the exciton as a function of the strain tuning for five QDs. (d) Real part of the density matrix of the two-photon state.[79] |
For most of the tuning techniques, it is impossible to realize the simultaneous tuning of FSS and the QD emission wavelength. As a consequence, it is difficult to realize an entanglement swapping between two separated QDs. In 2015, an in-plane strain tuning stage with three degrees of freedom, where the FSS and the exciton energy can be independently tuned, was theoretically investigated.[82] The proposed device is shown in Fig.
 | Fig. 15. (color online) (a) Sketch of the strains stage providing anisotropic in-plane strain fields. Three independent voltages (
|
In 2016, a six-legged piezoelectric device was realized experimentally by Trotta et al.[80] Polarization-entangled photons from InGaAs QDs were interfaced with a Cs vapor cell. After slowing down the photons by the atoms, a decrease in the entanglement fidelity was observed. This work opens the door to the realization of a hybrid quantum system based on semiconductor QDs. The device structure and entanglement fidelity are shown in Figs.
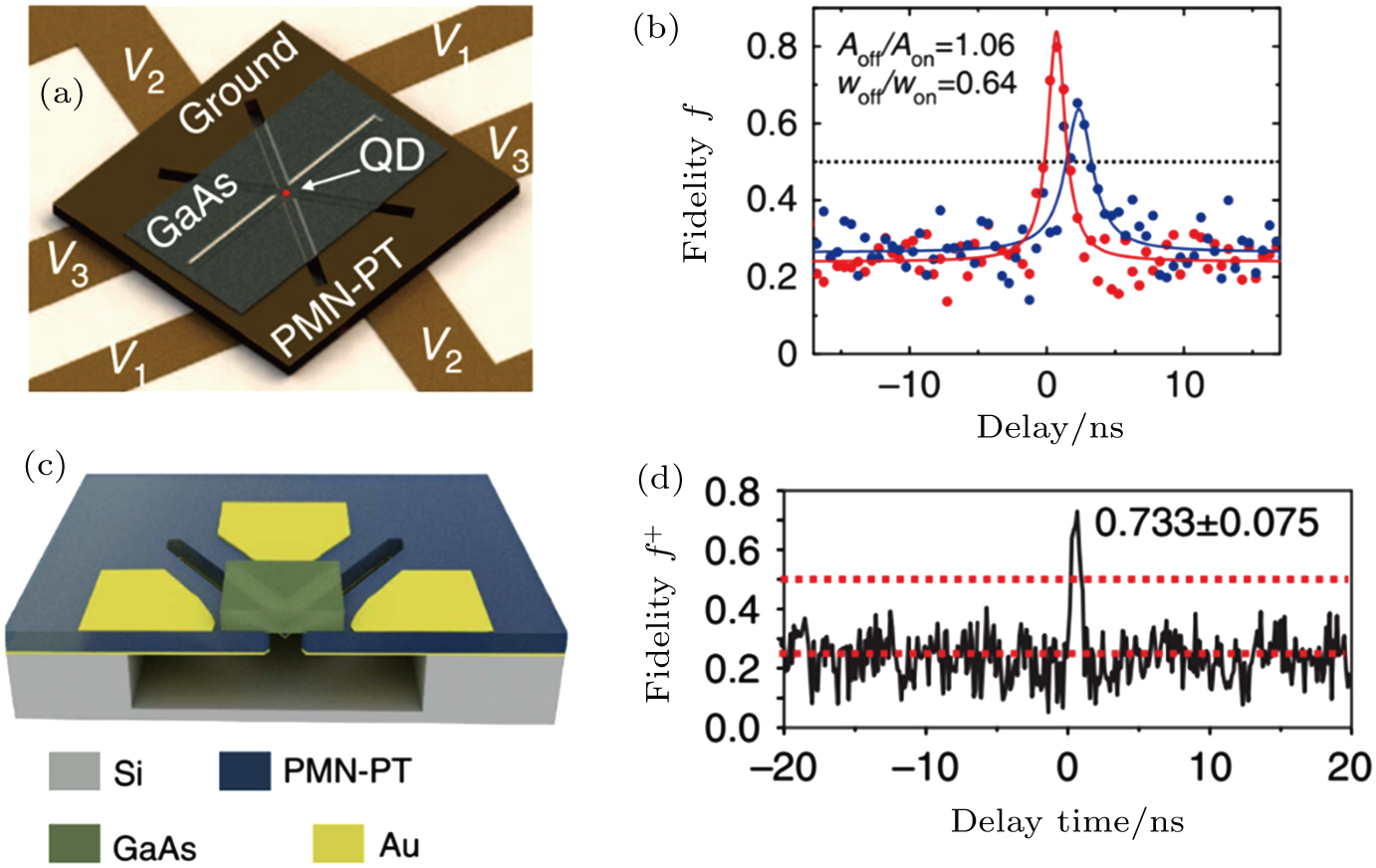 | Fig. 16. (color online) (a) Sketch of the six-legged strain tuning device used to engineer a nanomembrane (grey region) containing QDs. (b) Entanglement fidelity with (blue data points) and without (red data points) the Cs cell in the exciton optical path.[80] (c) Scheme of the cross section of the four-legged strain-tuning device. A focused ion beam (FIB) and a wet-chemical undercut were used to fabricate the device. A thin GaAs nanomembrane containing In(Ga)As QDs was transferred to the suspended region between the four legs.[83] (d) Entanglement fidelity results after the FSS tuning, without any background subtraction. |
To date, one of the most challenging tasks for QD-based PEPS is to enhance their brightness. Due to the high refractive index of the surrounding materials and isotropic emission of QDs, only a small portion of the photon pairs can be collected. The most common solution adopted to improve the extraction efficiency is to use the Purcell effect. When the QDs are coupled both spatially and spectrally with a cavity mode, their photon emissions are modified by
 |
An elegant solution was proposed by Dousse et al.[93] As shown in Fig.
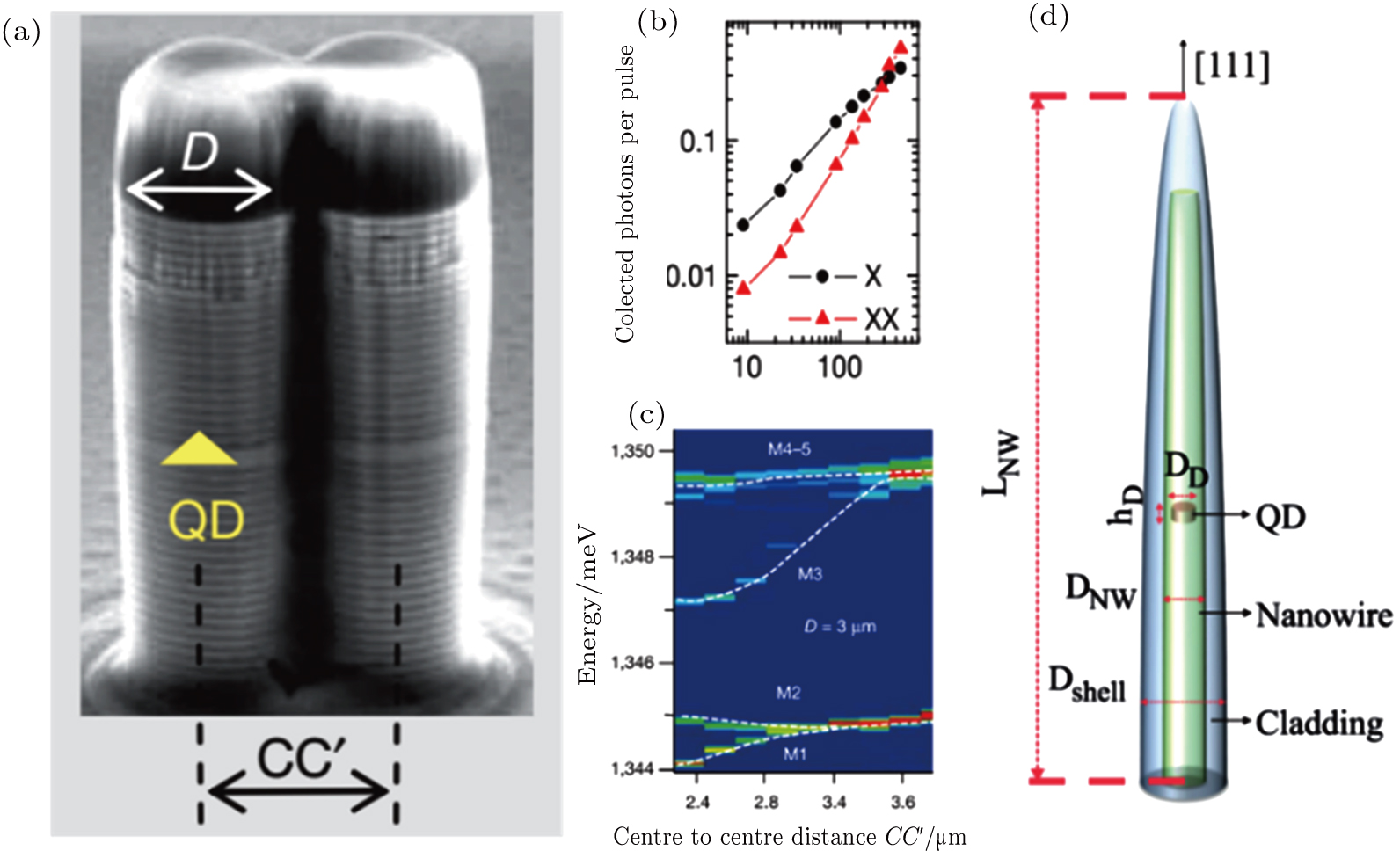 | Fig. 17. (color online) (a) Diagram of the device that contains two microcavities and one InAs QD. (b) Number of exciton and biexciton photons collected in each excitation pulse as a function of the excitation power. (c) The optical modes of the photonic molecule as a function of the intra-molecule distance.[93] (d) Structure of nanowire QDs.[95] |
An alternative option, which also brings a broadband enhancement, is to use the nanowire QDs. Versteegh et al.[94] reported that the nanowire waveguide has the advantages of a broad frequency bandwidth and a controlled direction, which suits for the QD-based PEPS. The light extraction efficiency of a single InAsP QD in InP nanowire could reach 18±3%. Besides, the entanglement fidelity to the maximum Bell state can be up to 0.765, without any time-gating technique. A similar work was reported by Huber et al.[95] The device structure is shown in Fig.
Semiconductor QDs can be excited either optically or electrically. The electrical injection is more promising in practical QIP, given that no sophisticated laser systems are required. The first ELED was realized by Salter et al.[97] They showed that the device could emit polarization-entangled photon pairs under DC or AC injections, with the latter achieving an entanglement fidelity of up to 0.82. After this pioneering work, it took the community a long time to reproduce the result, simply due to the low probability of finding QDs with small enough FSS. Zhang et al. reported a strain-tunable ELED,[79] as above mentioned. Another interesting recent work from Chung et al.[98] is based on the realization of selectively carrier-injected and site-controlled arrays of ELED based on pyramidal QDs.
For optical excitations, QDs can be excited either resonantly or non-resonantly. For the non-resonant excitation, the carriers are excited to energy levels higher than the first excited states, and they decay to the first excited states of QDs. In this scheme, an inevitable time jitter of the emissions is created. Besides, charges in excess will form around the QDs, leading to spectral diffusions and a pure dephasing. The combination of these effects will significantly degrade both the indistinguishability and coherence of the QD emissions. Moreover, the biexciton population probability under the non-resonant excitation is quite low. In 2014, Müller et al. realized a two-photon excitation (TPE) to single QDs via a virtual state.[99] The schematic is shown in Fig.
 | Fig. 18. (color online) (a) Energy diagram of TPE. (b) Photofluorescence spectra of the same QD, under non-resonant excitation (upper) and TPE (lower).[99] (c) Scheme of a pulse shaper to generate the chirp pulse (upper), and generation of a biexciton with broadband, chirped excitation (lower).[100] (d) Photofluorescence spectrum of a GaAs QD under phonon-assisted TPE for optimized detuning of the laser energy, pulse length (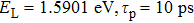
|
Figure
However, TPE is sensitive to the excitation power and the QDs’ environment, and a slight perturbation may lead to dramatic variations in the population probability. Reindl et al. reported a scheme called phonon-assisted TPE.[101] They claimed that, although the phonon-assisted TPE scheme is inherently non-resonant, the population inversion of exciton and biexciton states coupled to a quasi-continuum of vibrational modes is possible (see the inset of Fig.
Since the first realization of a QD-based entangled photon source in 2006, this field has experienced a significant success. The “on-demand” emissions of QDs make them a strong competitor of the traditional SPDC-based sources. To date, the FSS has been controlled through the methods mentioned above. There are also progresses in the on-chip integration, development of efficient excitation schemes, improvement of the photon indistinguishability, etc. However, several challenges remain to be overcome. For example, it is necessary to explore new material systems that function at higher or even room temperatures. In addition, the low brightness is a main hurdle. Recently, micro-lens fabricated with in-situ electron-beam lithography[103] and micro-objective made with a 3D-printing technique[104] have been used in QD-based single photon source. These interesting techniques can be exploited for the fabrication of QD-based PEPS. An efficient photon extraction from a QD may be also achieved with a broadband planar cavity antenna.[105]
For the application of PEPS, the entanglement swapping and purification protocols are important for an efficient distribution of the entanglement in a network.[106] Such protocols have been experimentally realized with SPDC sources.[107,108] Recently, the quantum secure direct communication has also been experimentally realized.[109,110] Thanks to the fast progress of QDs, we believe that QD-based PEPS will soon become an important workhorse for advanced quantum optics experiments.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] | |
| [100] | |
| [101] | |
| [102] | |
| [103] | |
| [104] | |
| [105] | |
| [106] | |
| [107] | |
| [108] | |
| [109] | |
| [110] |