† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61473166 and 41404146).
We investigate experimentally and numerically the quantitative dependence of characteristics of a low-velocity intensity source (LVIS) of atomic beam on light parameters, especially the polarization of cooling laser along the atomic beam axis (pushing beam). By changing the polarization of the pushing beam, the longitudinal mean velocity of a rubidium atomic beam can be tuned continuously from 10 to 20 m/s and the flux can range from 3 × 108 to 1 × 109 atoms/s, corresponding to the maximum sensitivity of the velocity with respect to the polarization angle of 20 (m/s)/rad and the mean sensitivity of flux of 1.2 × 109 (atoms/s)/rad. The mechanism is explained with a Monte-Carlo based numerical simulation method, which shows a qualitative agreement with the experimental result. This is also a demonstration of a method enabling the fast and continuous modulation of a low-velocity intense source of cold atomic beam on the velocity or flux, which can be used in many fields, like the development of a cold atomic beam interferometer and atom lithography.
Since the first demonstration of a laser-cooled atomic beam by Phillips and Metcalf,[1] a bright and cold atom beam has become the basis of many precise measurements and atom optic experiments, including ultra-high-resolution atomic and molecular spectroscopy,[2,3] atom frequency standards,[4,5] Bose–Einstein condensation (BEC) experiments,[6,7] atom interferometers,[8–12] atom lithography,[13] etc. The desirable features for a cold beam of neutral atoms are high flux at low average velocity, small divergence, tunability of flux and velocity, and robustness and stability in the beam parameters, which are especially important in our case, where a cold atomic beam of rubidium is directly used as a matter wave source for an atom interferometer.[14]
For obtaining a high-flux low-velocity atomic beam, two classes can be generally identified among the different schemes developed. One of the earliest methods is to start with a thermal beam and decelerate it along its propagation axis using radiation pressure in several methods, such as Zeeman slower,[1,15,16] frequency-chirped laser radiation,[15,17,18] isotropic light slowing,[19] and wideband light slowing.[4,20] Among these methods, Zeeman slowers are still widely used to give a high flux of atoms (about 1011 − 1012 atoms/s). However, the process of cooling by all these techniques is accompanied by associated photon heating, which induce unavoidable increase in the transverse temperature of atoms and hence a decrease in the beam brightness and phase space density.
The other class of methods more recently adopted is to use magneto-optic forces to first confine atoms in a vapor cell, which form a reservoir from which atoms can be efficiently ejected into a well-collimated beam. Vapor cells trade-off flux (about 109 − 1010 atoms/s) for the transverse compression of the atomic beam, a decrease in the longitudinal velocity of atoms and a reduced background of thermal atoms, but with similar flux density and a greater flexibility in design. The three most common vapor cell designs have been developed according to different configurations of magnetic and optical fields, including two-dimensional (2D) MOT,[9,21–25] 2D+ MOT[26–33] and its variations,[34–39] and 3D MOT or the LVIS.[40–43] Both the 2D+ MOT and LVIS designs use cooling and radiation force imbalance along the flux axis to produce a slow and narrow velocity distribution to several meters per second range, using a 2D and 3D quadrupole magnetic field, respectively. In the cases of the 2D MOT and 2D+ MOT design, the standard three-dimensional (3D) MOT arrangement in the source chamber is replaced by a 2D MOT configuration, with (2D+ MOT) or without (2D MOT) push and cooling beam along the symmetry axis. These techniques have been used for generating cold beams of different species of atoms and molecules from alkaline atoms (Li, Na, K, Rb, Cs) to the alkaline earths,[44] metastable helium,[45] and NH3 molecular.[46]
The choice of the method for producing a cold atomic beam depends on the specific requirements of the subsequent experiment. Most of these continuous cold atomic beam are eminently suitable for loading MOT, but are still very far from the ideal of a continuous beam with a controllable velocity, density, and temperature in the moving frame comparable to a pulsed cold atomic source based on an MOT in the application of an atom interferometer experiment. On one hand, flexible velocity or flux tunability is important for getting precise control or modulation on parameters of a matter-wave source for a well-defined de Broglie wavelength. On the other hand, these factors may lead to the instability of beam parameters of an atomic source, which induces phase noise of an atom interferometer. Several methods have been demonstrated for controlling the flux of an atomic beam and correspondingly the longitudinal velocity by changing the detuning of the cooling beam,[47,48] using separate “pushing” and “retarding” beams along the flux axis,[27] or two-color pushing beams.[36]
In this paper, we study the characteristics of an LVIS atom beam as a function of light beam parameters, especially the pushing light polarization. A 87Rb atomic beam is prepared and experimentally measured for this aim and a numerical simulation based on the Monte Carlo method is used to explain our results qualitatively. Results show that pushing beam polarization angle may influence the longitudinal velocity and flux of an LVIS atomic beam with the sensitivity of 20 (m/s)/rad and 1.2 × 109 (atoms/s)/rad, respectively. This also presents a simple method which enables fast modulation of an LVIS atomic beam on the longitudinal mean velocity ranging continuously from 10 to 20 m/s by changing the polarization of the pushing beam.
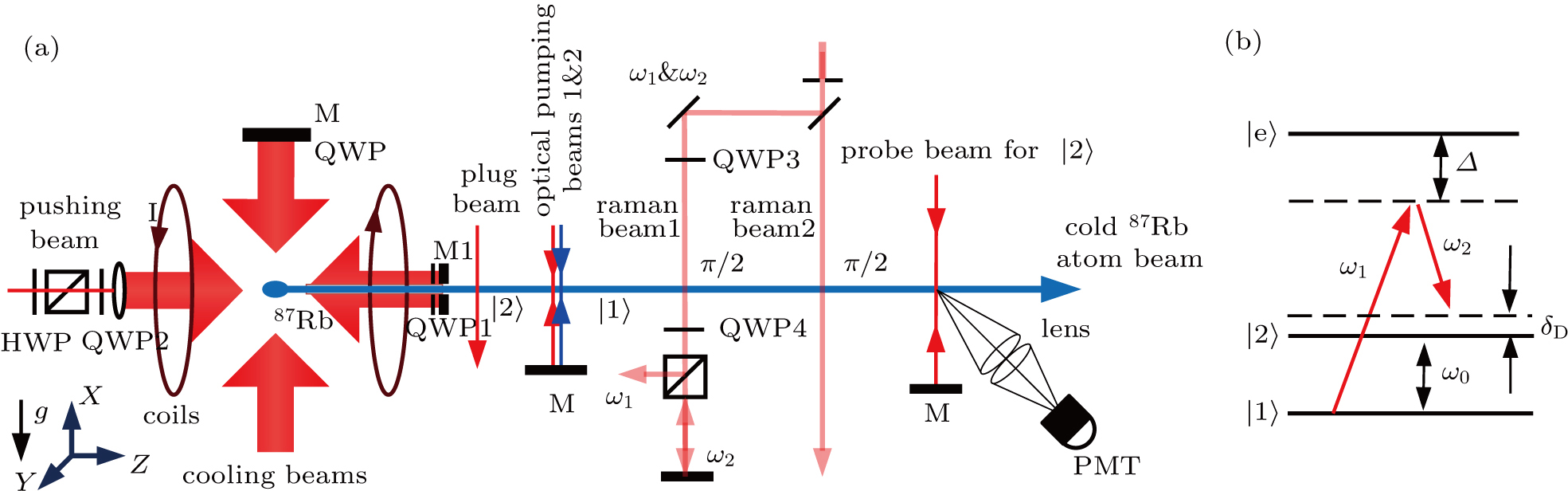
A diagram of the experimental setup is shown in Fig.
The longitudinal velocity and flux of the cold atomic beam are measured by the time-of-flight (TOF) method, realized by switching off the atomic beam using a plug beam. The fluorescence of atoms, induced by a probe laser beam, is collected by a photomultiplier tube (PMT, H7422-50, Hamamatsu, Japan) in a distance of 0.7 m from the plug beam. Both the plug beam and probe beam are tuned to the F = 2 → F′ = 3 resonance.
The transverse velocity distribution of the cold atomic beam is measured by the two-photon velocity-selective Raman transitions.[49] When a pair of counter-propagation Raman beams, in Doppler-insensitive geometries, meet at right angle with the atomic beam, the detuning frequency of Raman beam, δD, is related to the transverse velocity vx,
As shown in Fig.
Before interacting with the Raman beams, the atoms initiated in the F = 2 ground state need to be state-prepared to the magnetically insensitive |F = 1, mF = 0⟩ ground state by a combination of optical pumping beams 1 and 2, which are tuned to F = 2 → F′ = 2 allowed transition and F = 1 → F′ = 0 in σ± transitions (linear polarization orthogonal to the magnetic field), respectively. In addition, a constant magnetic bias field is applied throughout the length of the second chamber to define a quantization axis, horizontally in the direction of the Raman beams, with a four-conductor magnetic field assembly running inside the vacuum chamber (not shown in Fig.
A numerical simulation based on the Monte Carlo method is carried out to model the atomic beam characteristics in a similar approach used by Chaudhuri et al.[33] The simulation considers motion equations of atoms, which are captured from the background vapor in a 3D MOT, form into a beam under the imbalanced radiation pressure, and then pass through a hole into the next UHV chamber where the beam flux is measured.
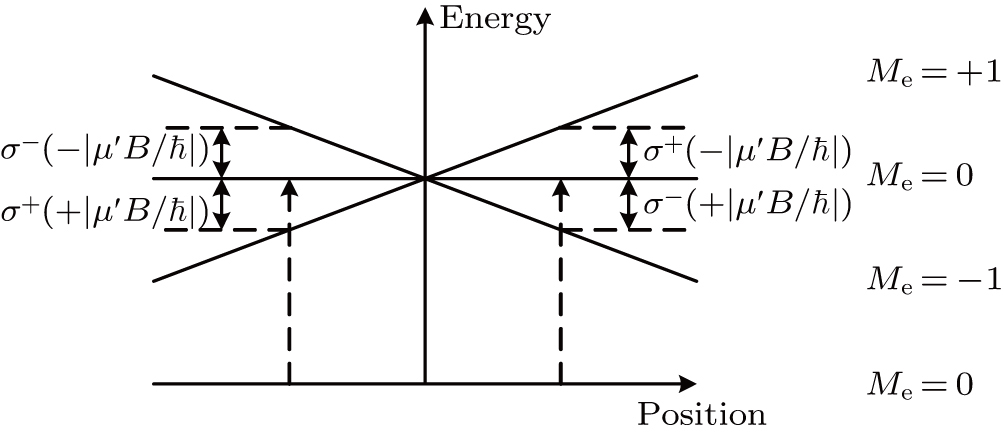
For the description of motion of atoms in an MOT, we consider the scattering force on atoms in the low-intensity limit. The total scattering force on an atom is given by 
The frequency detuning from resonance, δ±, for each laser beam is given by
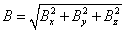
Equation (
Equation (
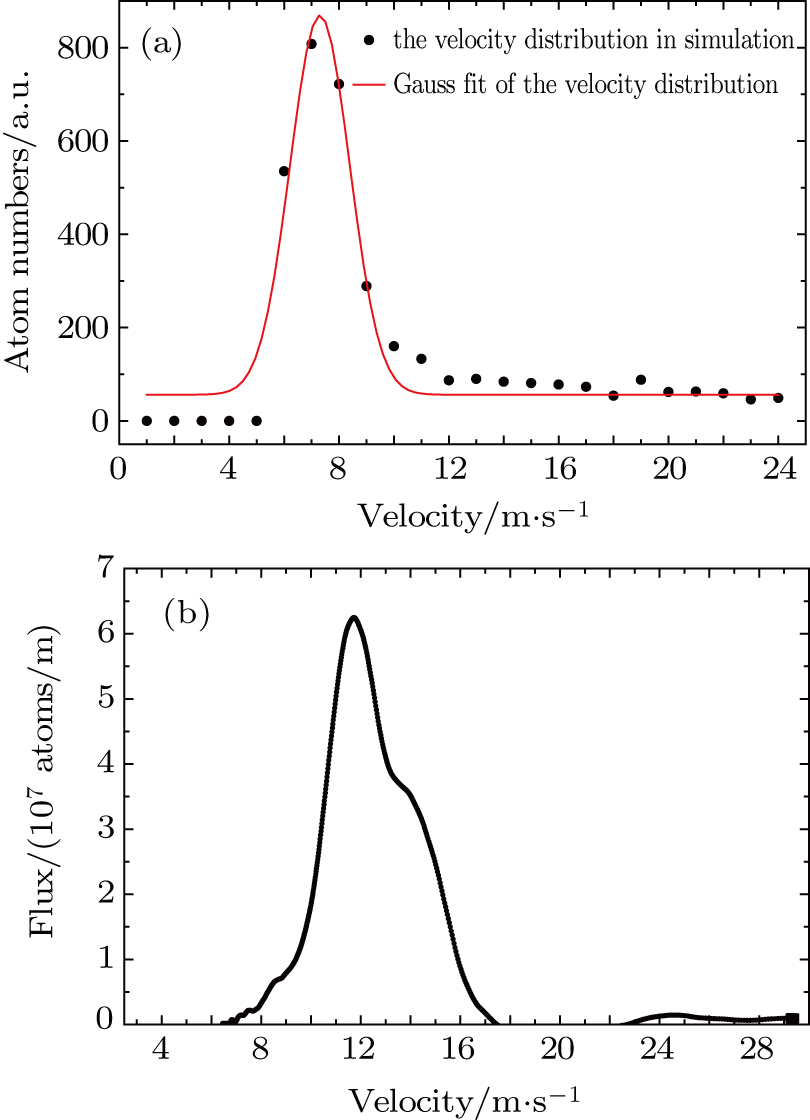
Starting with an initial sample of 1 × 107 atoms, we compute their individual trajectories and obtain the fraction of atoms being captured and transferred into the atomic beam. Trajectories of 1000 atoms calculated by a 3D numerical simulation are shown in Fig.
We simulate numerically and measure experimentally various beam characteristics of atoms, especially the atomic beam flux and longitudinal velocity as functions of the cooling beam detuning or the pushing beam polarization. One simulated velocity distribution of an atomic beam extracted from the LVIS and the corresponding experimental result are shown in Fig.
Atomic beam characteristics generated in the LVIS are studied with respect to variation of the pushing beam polarization by rotating the quarter-wave plate QWP2. Experimental and simulation results are shown in Fig.
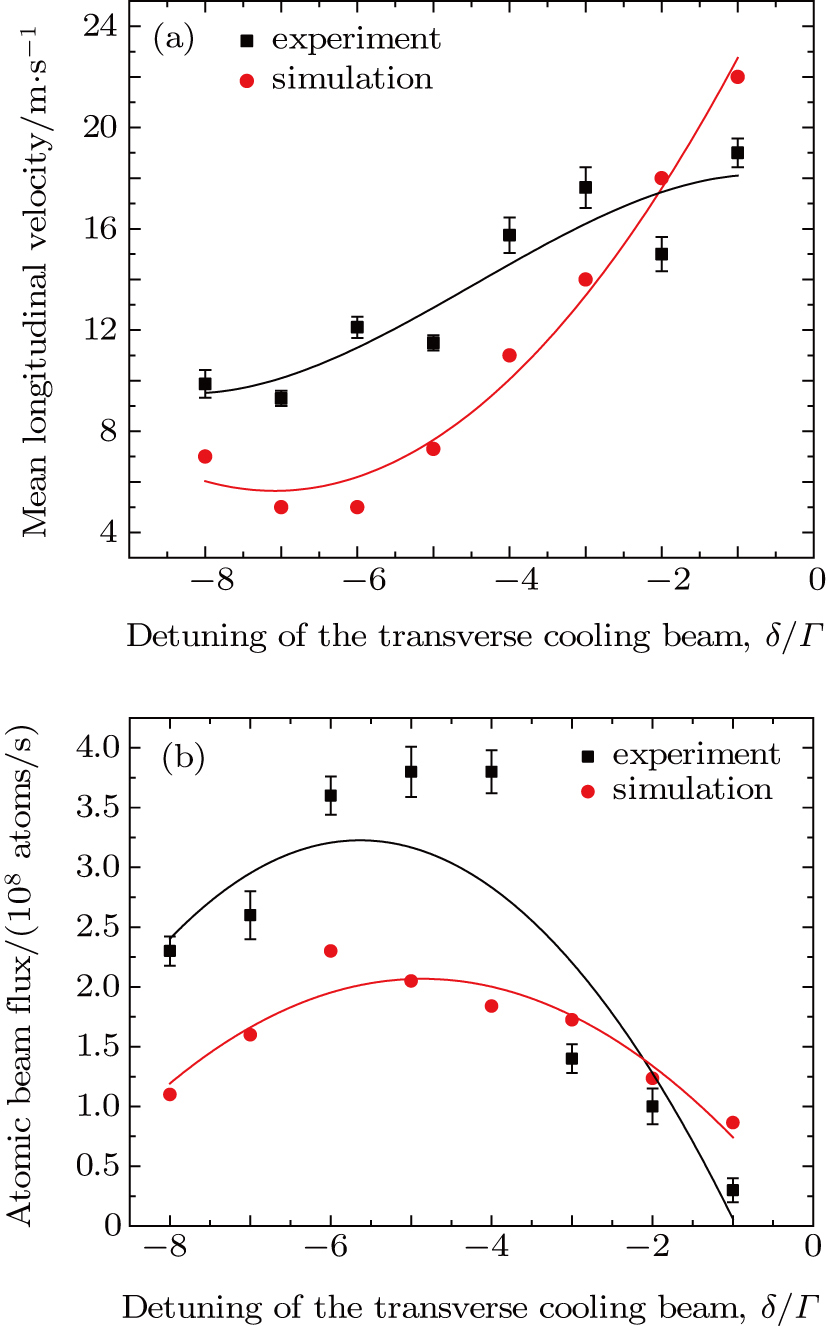
The variation of atomic beam characteristics is also studied as a function of frequency detuning of the transverse cooling laser. Experimental and numerical data are shown in Fig.
Transverse velocity spread is measured by the Doppler-sensitive Raman transition spectrum. The Doppler-sensitive Raman transition spectra driven by the first π/2 Raman pulse by blocking the Raman beam 2 shown in Fig.
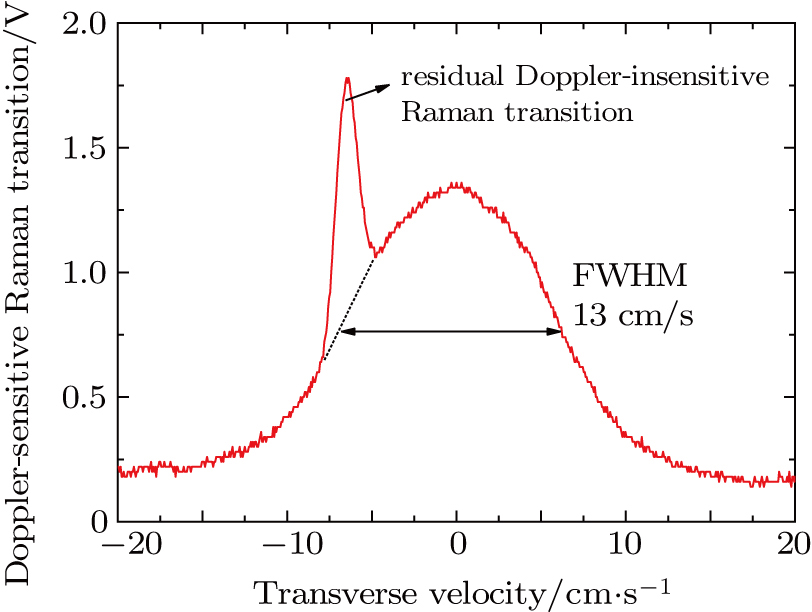 | Fig. 7. (color online) Doppler-sensitive Raman transition spectrum for measuring transverse velocity spread. |
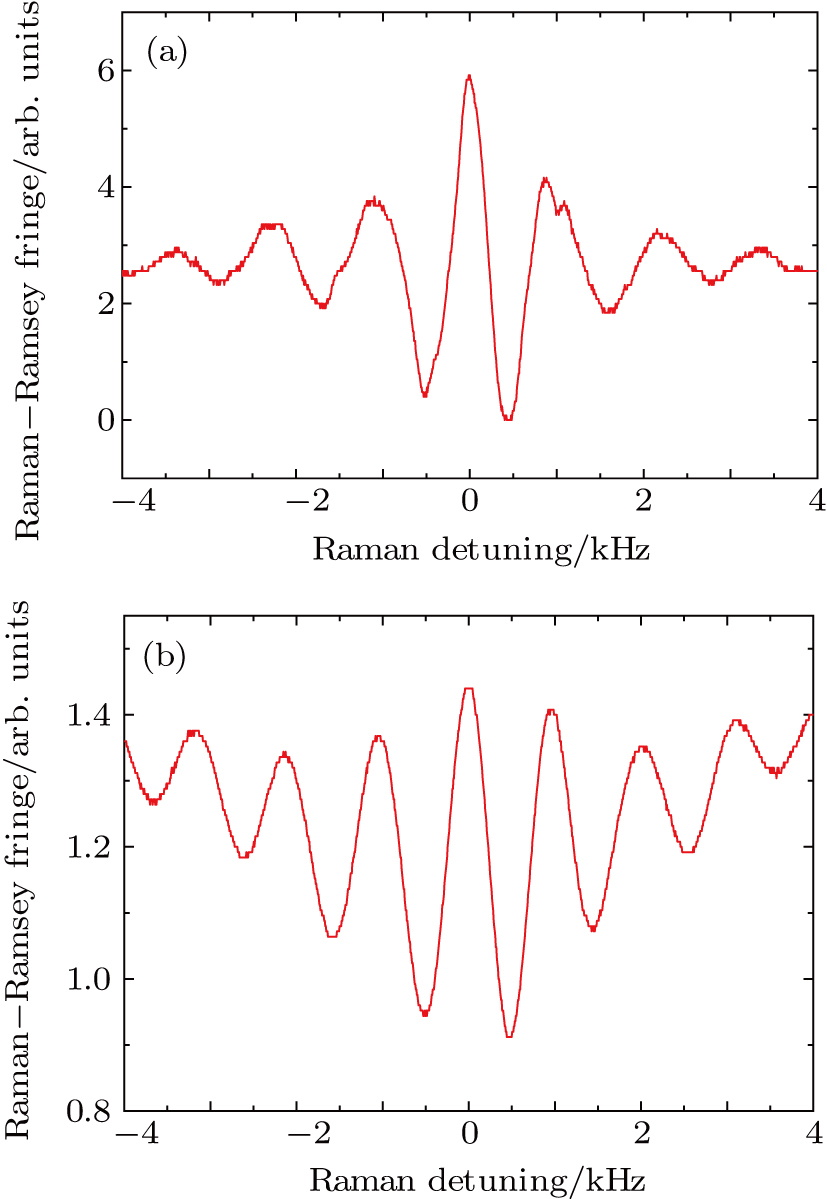
The tunability of the velocity and flux of a continuous LVIS atomic beam are demonstrated in a Raman–Ramsey atomic interferometer by changing the polarization of the pushing beam. With the π/2–π/2 pulse sequence, we obtain the Raman–Ramsey fringes with an interaction-zone separation of L = 19 mm and an interaction-zone width of d = 1 mm. The Raman–Ramsey fringes with different longitudinal velocity of the atomic beam are shown in Fig.
In conclusion, we study experimentally and numerically the quantitative dependence of an LVIS of atomic beam on the polarization of the pushing light beam. Results show that the pushing light polarization is an important factor to influence the flux and velocity of an LVIS atomic beam, with maximum sensitivity with respect to the polarization angle of 1.2 × 109 (atoms/s)/rad and 20 (m/s)/rad, respectively. For an atom interferometer rotating at an angular velocity Ω, the phase shift can be written as ΔΦΩ = 


Although we have demonstrated that the pushing beam polarization is one of the important factors that influence the characteristics of an LVIS of an atomic beam, the improvement of the stability of an LVIS of atomic beam depends on the systematic optimization involving many experimental parameters like light intensity, frequency detuning, etc. Concerned with the pushing beam polarization, one can make the LVIS source operate in the polarization-insensitive range or take some active method for stabilizing the polarization. On the other hand, one can fast tune the velocity and flux of an LVIS-based atomic beam by simply changing the polarization of the pushing light for actively stabilizing the atomic beam source or amplitude modulating and demodulating the phase of an atomic beam interferometer to get interferometer signal with higher signal-to-noise ratio.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] |