† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11275238, 11205225, and 11375034).
Simulations of guiding of low-energy ions through a single nanocapillary in insulating polymers are reported. The nanocapillary has a diameter of 100 nm and a length of 10 μm. Different from previous work, in our simulations a hyperbolic function is used to describe the decay of the charges deposited on the capillary surface. The present simulations reproduce the self-organized charge-up process occurring in the capillary. It is shown that lower-energy ions undergo more oscillations to get guiding equilibrium than those of higher-energy ions, resulting in a longer charging time, which is in good agreement with previous experimental results. Moreover, the experimentally observed mass independence of ion guiding is proved in our simulations. In particular, it is found that the maximum of the repulsive field within the capillary is independent of the ion energy as well as the tilt angle. To counterbalance the increasing of the transversal energy caused by increasing the tilt angle or incident energy, the effective length of the repulsive field is expanded in a self-organizing manner.
Over the past decade, the interactions of low-energy ions with the insulating capillaries have been extensively studied. Unlike the phenomena occurring in the metal capillaries,[1] ions can be transmitted along the insulating capillary axis with their initial charge state and incident energy even when the capillaries are tilted by a larger angle with respect to the incident ion-beam direction.[2–5] This phenomenon is called ion guiding, which is attributed to the self-organized formation of charge patches on the capillary internal wall.[2,6]
The guiding process can be qualitatively described as follows: Ions entering into the capillary tilted by an angle hit the wall and, in turn, deposit their charges at the collision points so that a charge patch is generated near the entrance region (hereafter referred as to entrance charge patch). When the entrance charge patch is sufficient to produce a strong repulsive electric field, subsequent ions will be deflected at large distances from the capillary wall. As a result, the close collisions and charge exchanges between ions and atoms on the capillary wall are inhibited. Then, additional small charge patches are formed further inside the capillary.[6–12] Owing to the capillary conductivities, the entrance charge patch is extended and the small charge patches are strongly weakened so that the electric field within the capillary keeps unchanged to maintain ion guiding.[8,11,12]
Experimentally, a large number of researchers have studied the guiding effect using different insulating capillaries[2–6,13–16] accompanied by negative ions,[17–19] molecular ions,[20,21] and electrons,[22,23] as well as various positive ions. Through analysis of various experimental results, many outstanding achievements are acquired. For instance, the observed oscillations of the ion emission angle provide evidence of sequential charge patches formed on the capillary internal wall.[6,24] Particularly, it is found that the guided transmission are not dependent of the ion mass but primarily dependent of the projectile charge-to-energy ratio.[25,26] Recent experiments reported that 1-MeV proton microbeam could be guided through a single cylindrical Teflon macrocapillary,[27] which still needs further interpretations.
Motivated by the desire to understand the guiding mechanisms, theoretical investigations by means of Monte Carlo simulations.[8–12,28] and analytic calculations[29] have been performed in several research groups. These theoretical studies successfully provide more detailed information about ion guiding. It is demonstrated that most of the deposited charges are located near the entrance region.[9–12] To establish ion-guiding equilibrium in simulations, the transport of charges deposited on the capillary wall should be invoked. However, there exist two different models of the charge transport used in previous simulations, namely the drift model[8,11,12] introducing a nonlinear effect on the charge migration in an electric field, and the diffusion model[9,10] adopting an unbiased random walk to describe the spread and depletion of the deposited charges. Here, it should be pointed out that some general properties of ion guiding can be reproduced by either of these two models. Therefore, a deeper understanding of guiding process within the capillary is still needed. A review on both the experimental measurements and theoretical description of the capillary guiding can be found in Refs. [30] and [31].
The present work is primarily intended to simulate the transmission of ions guided through a nanocapillary and to compare the simulated results with those reported previously. The program is written in MATLAB language which can simplify the procedure codes and improve the developing efficiency greatly. Section
The simulations were designed to explore ion guiding through a cylindrical nanocapillary in polyethylene terephthalate (PET) materials. The nanocapillary has a diameter of 100 nm and a length of 10 μm, whose geometric illustration is shown in Fig.
The simulation methods are very similar to those used in Refs. [9]–[12] except for the charge transport caused by the capillary conductivities, so that the overlapped part are outlined briefly. The capillary wall becomes charged due to the deposition of incident ions but without considering the addition charge-up via the secondary electron emission induced by the ion impact with the capillary wall. The trajectories of ions under the function of electric fields produced by the charged wall, are determined by solving Newton’s equation of motion. Note that the electric fields are weakened by the image charge of the deposited charges.[35,36] For PET materials with relative permittivity ε ≃ 3.2,[37] the electric fields are reduced by a factor of (1 + ε)/2 ≃ 2. Here, it should be pointed out that since we use a single nanocapillary to simulate ion guiding, influences of the capillary neighbors are neglected. Nevertheless, this neglect is justified when the number of capillaries per unit area in foils is not very high.[38]
Due to the capillary conductivities, the charges deposited on the capillary wall will undergo spread and decay, which is key to the guiding process. Since the surface conductivity is much larger than the bulk,[9] only the spread along the capillary surface is taken into account in our simulations. In addition, compared to the drift mechanism, the effect of the diffusion on the charge transport is rather minor.[32] Hence, in our simulations, the diffusion is not invoked.
The spread of deposited charges is considered in terms of the built-in electric field-driven migrations. It is assumed that the charges reaching the golden layer on the front and back surface of the capillary foil will disappear immediately. The carrier mobility governing the charge migration is found to exponentially depend on the square root of the electric field,[39] which is similar to the conductivity modeled by Poole–Frenkel mechanism.[40] To date, it is ambiguous for us whether these two dependencies are exactly within the same framework. Therefore, to avoid the possible inconsistencies, we directly quote the empirical expression for the mobility introduced in Ref. [39], namely,
 |
 |
It is obtained from Ref. [41] that the mobility μ0 of electrons in Mylar (PET) foil is in the neighborhood of 1 nm2/(V·s). Unlike the treatment of the ion deposition in Ref. [11], we assume that the ion deposited on the capillary wall would become an ion-carrier determining the position of the deposited ion. Accordingly, the mobility for ions is estimated to be smaller than the value of 1 nm2/(V·s) as a result of the heavy mass. However, as pointed out in Ref. [11], the mobilities in insulating materials have large uncertainties spanning more than eight orders of magnitude since they are in close relation to the treatment of the internal surface of the hole, such as the humidity, cleanliness.[37,42] Thus, it is unlikely to directly use these mobilities in the simulations. Our methods of determining the mobility is to test the calculations with values varying from 1 nm2/V·s to 10−4 nm2/V·s, and then find the optimal one by comparing the calculated results to the previous experiments of the capillary guiding. After some tests, it is found that the μ0 value of 10−4 nm2/V·s is appropriate for Ne7+-ion guiding. The test results are presented in Appendix
Then, combining the field
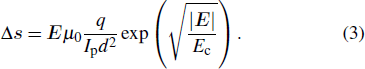 |
Equation (
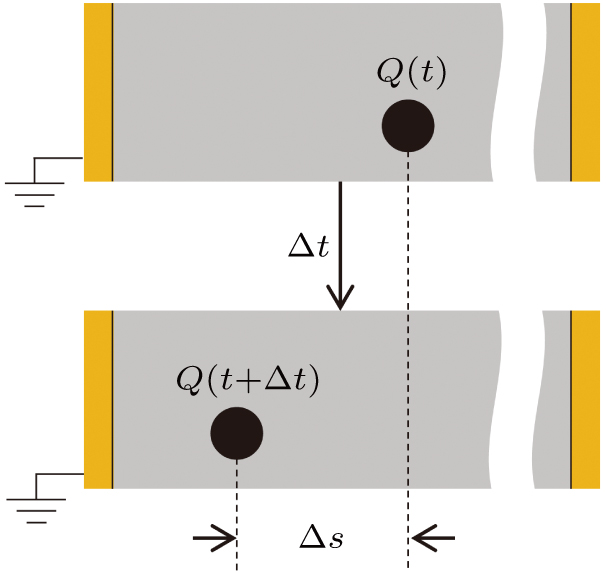 | Fig. 2. (color online) The deposited charge Q(t) is changed into Q (t + Δt) after a time Δt, and the position is governed by Eq. ( |
In previous simulations,[10,11] the decay of the deposited charge Q(t) is assumed to follow an exponential law to describe the charge diffusion into the capillary bulk. However, as mentioned in Refs. [9]–[12] the bulk conductivity could be neglected compared to the surface conductivity. That is to say, the bulk discharge cannot have a significant impact on guided transmission. Moreover, the guiding experiments[43] exactly claim the charge decay not to be exponential with time. Fortunately, it has been achieved in early studies[32–34] that the charge decay on the insulating surface obeys the following hyperbolic formula:
 |
Since both equations (
 | Fig. 3. (color online) The decay of a uniformly charged plate simulated by using Eq. ( |
The selection of ions and the beam currents, to some extent, is subjective. However, one of the selection criteria is that the ion and the current should be readily available from previous experiments for sake of assessing the precision of our simulations. Besides, on the premise of saving the computing time, the selection is best not to introduce extra approximations and simplifications. Therefore, Ne7+ ions with current of 200 pA/mm2 is selected, which leads to that the number of Ne7+ ions injected into the capillary per second is the equivalent of about 1 with consideration of dielectric screening. To make the simulations more factual, the divergence of incident beam is set to be 0.3° full width at half maximum (FWHM) estimated in previous experiments.[20,44] Here, it is added that we can not explain from first principles why the values of the parameters μ0 and t0 should, respectively, be 10−4 nm2/V·s and 1000 s but simply take them as empirical fact that turns out to agree with the experimental observations reported before.
Now, we proceed to the simulations with considering the capillary conductivities. During simulations, the charge migrations on the capillary wall were calculated by Eq. (
From Fig.
Comparing Figs.
 |
For comparison of the absolute values of the charging time τc = 17.1 min with experiments, a review of the literature was conducted. It was found that for 3-keV Ne7+ ions through PET capillaries with 100-nm diameter and 10-μm length tilted by angle of 5°, it needs deposited charge Qc ≃ 350 nC (Qc = Ip · τc) to reach equilibrium.[46] In our simulations, the deposited charge Qc is about 205 nC (200 pA × 17.1 min), which is reasonable in view of the fact that the tilt angle is not the same. Moreover, various currents also result in different Qc values.[47]
In order to search the influence of the ion mass on guided transmission, various species of ions were used as projectiles in simulations. Therefore, we studied the fractions of ions transmitted through the nanocapillary. Figure
 | Fig. 6. (color online) Transmitted ion fractions of Ne7+, Ar7+, Kr7+, and Xe7+ ions with energy of 7-keV and 1-keV Ne1+. The solid lines represent fits through the simulated data using Eq. ( |
According to the foregoing mention, the time evolution of the ion faction with time is governed by the characteristic time τc and the equilibrium faction f∞ indicated in Eq. (
| Table 1.
Values of parameters τc, τs, and f∞ for different ions. . |
For understanding details of guiding mechanism, we studied the field at guiding equilibrium. It is found that the field component Ex is always zero only with small fluctuations, which implies the symmetric distributions of the deposited charges. Similar to the field Ex, the field component Ez is nearly zero except for that near the capillary entrance. This nonzero Ez whose direction is along the negative z axis, would drift the deposited charges near the capillary entrance to the golden layer and, in turn, gives rise to discharging. Therefore, in the following the attention is focused on the field component Ey which is responsible for the ion deflections within the capillary.
Figure
Moreover, the effective length (the part of nonzero values) of the field component Ey increases with the tilt angle, in agreement with previous work.[12] This finding implies that the length of the field should expand in direction of the capillary axis to counterbalance the increasing of the tilt angle. In particular, it is found from comparison of Figs.
In summary, the present simulations capture the essential features of the ion transmission guided through the insulating nanocapillary. The simulations indicate that the ions undergo oscillatory trajectories to the exit of the capillary, which result from the several charge patches sequentially formed on the capillary internal surface. Moreover, it needs a longer time for lower-energy ions to get guiding equilibrium as a result of more oscillations, in agreement with the experiments.[45]
On the other hand, the simulations provide direct evidence that the transmission of ions guided through the insulating capillary is nearly independent of ion mass. As expected by the semiempirical scaling law,[25,26] the key controlling parameter of ion guiding is the ratio of charge to energy. This implies that the insulating capillary has pretty promising future in manipulating various charged particles regardless of the mass.
Most importantly, the field component Ey is found to be nearly unchanged by varying the ion energy as well as the tilt angle. Hence, to guide ions with high transversal energy caused by the increasing of the tilt angle or incident energy, the effective length of the field Ey is extended in a self-organized manner.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] |





