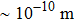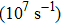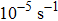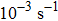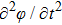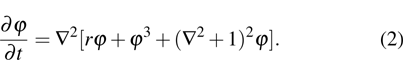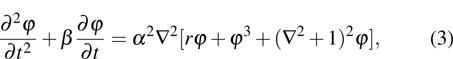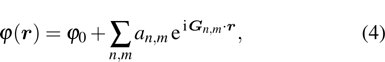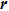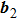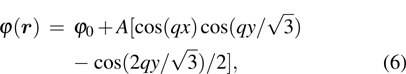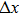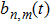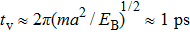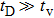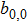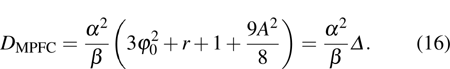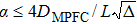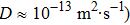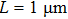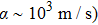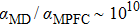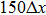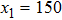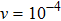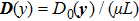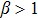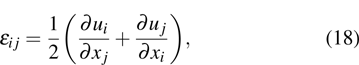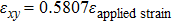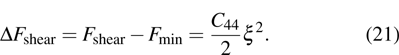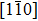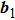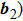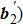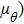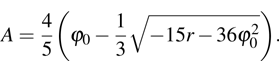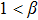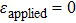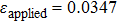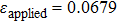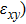1. IntroductionThe elasticity of materials is important for understanding processes ranging from the propagation of elastic waves, to flexure, and to brittle failure.[1–4] A complete parameterization of elastic properties in experiments is however challenging, especially for the deformation of a solid which operates across several length and time scales. Usually, the elastic deformation dynamics on atomic length (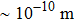 ) and time (
) and time ( ) scales can be captured by molecular dynamics (MD) simulations.[5] However, due to very short time scales, only high stresses (GPa) and strain rates
) scales can be captured by molecular dynamics (MD) simulations.[5] However, due to very short time scales, only high stresses (GPa) and strain rates 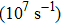 can be probed in the dynamical deformation process. These are to be contrasted with much slower experimental strain rates of
can be probed in the dynamical deformation process. These are to be contrasted with much slower experimental strain rates of 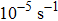 to
to 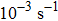 .[6]
.[6]
Recently, based on the density functional theory,[7] Elder and Grant[8,9] proposed a new methodology, called the phase field crystal (PFC) model, which provides a natural description of slow, diffusive dynamics in interacting systems while still maintaining the atomic-level resolution, including topological defects, elasticity, and plasticity. This method has powerful capabilities in describing polycrystalline solidification,[10,11] phase transitions,[12] vacancy diffusion dynamics,[13] dislocation (annihilation, glides and climb),[14,15] and fracture.[16,17] As to the elasticity and plasticity behaviors,[18,19] the PFC method can also describe mechanical responses at low stress and low steady-state strain rate. Considering that the original PFC model did not contain a mechanism for describing elastic interactions sufficiently, Stefanovic et al.[18,20,21] proposed a modified phase-field-crystal (MPFC) model in which the corresponding dynamic equation includes the inertia effect or wave-like term 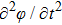 originated from the second order term of time. Thus this MPFC can facilitate rapid elastic relaxations. After comparing results from MPFC to those from PFC, Stefanovic et al. found that the elastic relaxation presented in the MPFC is consistent with the linear elasticity theory. However, the details of a parameter interval for the elasticity behavior are still lacking and how the crystal lattice orientation or system temperature influences the elastic coefficients is also unclear. Therefore, in this work, we first investigate the elastodynamic response of the MPFC model by analyzing the deformation behavior of a strained nano-single crystal specimen, and then we quantitatively characterize the strain distribution of the specimen and analyze the effects of the initial crystal lattice orientation and temperature on the shear modulus. One of the primary goals of this work is to gain new physical insight into these problems, which will prompt the MPFC method as a predictive tool to capture the elastic response of atomic properties for more complicated real materials.
originated from the second order term of time. Thus this MPFC can facilitate rapid elastic relaxations. After comparing results from MPFC to those from PFC, Stefanovic et al. found that the elastic relaxation presented in the MPFC is consistent with the linear elasticity theory. However, the details of a parameter interval for the elasticity behavior are still lacking and how the crystal lattice orientation or system temperature influences the elastic coefficients is also unclear. Therefore, in this work, we first investigate the elastodynamic response of the MPFC model by analyzing the deformation behavior of a strained nano-single crystal specimen, and then we quantitatively characterize the strain distribution of the specimen and analyze the effects of the initial crystal lattice orientation and temperature on the shear modulus. One of the primary goals of this work is to gain new physical insight into these problems, which will prompt the MPFC method as a predictive tool to capture the elastic response of atomic properties for more complicated real materials.
2. Model description and strain characterization2.1. The MPFC modelThe PFC model was introduced to describe periodic systems of a continuum field and can naturally incorporate elastic and plastic behaviors. It relies on a well-known Swift–Hohenberg (SH) form free energy functional and an overdamped equation of motion in describing the temporal evolution of the field φ that represents the reduced local particle density. The simplest dimensionless PFC model for pure systems follows as a conserved evolution of the free energy
where the order parameter
φ is the atom number density field measured from a constant reference value, and
r is a phenomenological constant related to the temperature.
The standard dimensionless evolution kinetic equation for the order parameter φ is
The above kinetic equation describes time scales in crystals near and beyond that of the characteristic vacancy diffusion time. It does not, however, allow any collective atomic oscillations, which are on a much faster time scale. This omission of elastic interactions in the model prevents us from studying phenomena involving several time scales of various orders of magnitude (such as the deformation dynamics of nanocrystalline solids). To tackle this problem, the MPFC dynamic equation is introduced by adding a second order time derivative to the equation
[18]
where
α and
β are phenomenological constants related to the effective sound speed and vacancy diffusion coefficient, respectively. Equation (
3) is of the form of a damped wave equation, and it supports two density propagating solutions: one diffusional and the other corresponding to a propagation elastic mode. By choosing effective values of
α and
β, finite elastic interaction length and time can be set.
The thermodynamic properties of the PFC model have been discussed previously,[8,9,22] indicating that this model can yield different crystal phases, such as body-centered-crystal lattices, hexagonal lattices, and lamellar phase. The periodic order parameter φ can be written in the general form
where

is the amplitude of the atomic density,
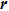
is the space position vector, and
φ0 is the average atomic density.

, where

and
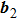
are the reciprocal lattice vectors. For two-dimensional (2D) hexagonal lattices, these reciprocal lattice vectors can be written as
where
a0 is the crystal lattice constant. Here we employ one-mode approximation to keep the only critical mode whose amplitude is equal to

(
A is the amplitude of the density waves). The hexagonal lattice density in two dimensions is acquired as
where
q is the wave number related to
a0, satisfying

. Substituting Eq. (
6) into Eq. (
1), integrating over a unit cell, and minimizing the free energy with respect to
A and
q lead to
The physical details of all parameters and the solving procedure of Eq. (3) spectrally implemented in the Fourier space can be referenced to Ref. [23]. Here, unless otherwise specified, all parameters used in the simulation are
where
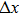
and

are the grid-sizes and

is the time-step size.
2.2. The elastodynamic response in the MPFC modelIf we consider a perfect lattice with one “atom” chopped out, this would correspond to a vacancy in the lattice. Phonon vibrations would occasionally cause neighboring atoms to jump into the vacancy and eventually the vacancy would diffuse through the lattice. In the PFC model, the density at the vacancy slowly fills in and the density at the neighboring sites slowly decreases as the vacancy diffuses throughout the lattice. To determine time scales of vacancy diffusion, it is useful to perform a linear stability analysis,[24] which linearizes Eq. (2) around an equilibrium state density field  according to
according to
where

is a perturbation wave vector and
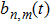
is the corresponding amplitude associated with the perturbation of the steady-state mode

. The resulting linearized equation of Eq. (
2) is obtained by substituting Eqs. (
9)–(
11) into Eq. (
2) and expanding the latter to linear order. Then the diffusion constant can be obtained as
This analysis demonstrates that equation (
2) admits propagating solutions for density disturbances with an effective diffusion time

, which can be written as
Take Cu at 1063 °C as an example. With a lattice parameter of
a = 3.61 Å and the self-diffusivity

, it will take about

for an atom to diffuse to its original nearest neighbor position. On the other hand, the bond stretch “vibrational period”
[25] is estimated to be
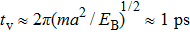
, where

is the atom mass and

is the binding energy due to the interatomic potential. So
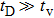
, note that the diffusive motion of an atom in the crystalline phase is much larger than the elastodynamic response time of the vibrational motion of an atom. This suggests that elastic strains will relax instantly, implying that the system would correspond to an over-damped system, which prevents PFC simulation from direct comparison with faster, real-world mechanical experiments. In order to overcome this deficiency, the MPFC model was introduced to make the PFC model operating on two time scales: one diffusional and the other corresponding to a propagating elastic mode.
[18]To better understand the diffusive dynamics and elastic interactions governed by the MPFC equation, a linear stability analysis is performed. The linearized equations are the same as Eqs. (9)–(11). It is straightforward to repeat the above calculation in the PFC model. Substitute Eqs. (9)–(11) into Eq. (3) and ignore higher-order nonlocal terms retaining only the contribution 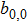 among the nonlinear coupling terms with zero modes. By solving the resulting linearized dynamic equation, the effective elastic interaction length and interaction time can be obtained (see Ref. [18] for details)
among the nonlinear coupling terms with zero modes. By solving the resulting linearized dynamic equation, the effective elastic interaction length and interaction time can be obtained (see Ref. [18] for details)
where

. Moreover, the effective vacancy diffusion coefficient reads
By properly tuning the parameters α and β, finite elastic interaction length and time can be set. Over this elastic interaction time and distance, the density waves will propagate effectively undamped. Beyond this time and distance, however, the density evolution becomes diffusive. As an illustration, considering a system with dimension L, we require the elastic interaction length  , which implies
, which implies 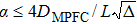 . After choosing an appropriate value for α, β can be determined from
. After choosing an appropriate value for α, β can be determined from  . Using Cu at 1063 °C as an example (
. Using Cu at 1063 °C as an example (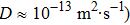 and the computational domain
and the computational domain 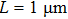 , one would choose the effective sound speed
, one would choose the effective sound speed  and the effective vacancy diffusion coefficient
and the effective vacancy diffusion coefficient  . If we compare this sound speed with that in the classical MD simulations (
. If we compare this sound speed with that in the classical MD simulations (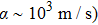 , we can obtain
, we can obtain 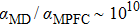 , implying that MD is 1010 times faster.
, implying that MD is 1010 times faster.
In short, the MPFC approach takes advantage of the fact that elastic relaxation does not need to be instantaneous due to a separation of elastic relaxation and diffusion time scales.
3. Results and discussionIn this section, several simulation results are shown to demonstrate the abilities of MPFC formulation in describing the elasticity response at atomistic scales. Firstly, we will discuss the shear deformation response of the MPFC model, and then examine the elastic response of a nano-single crystal. Finally, the orientation and temperature dependence of the shear modulus will also be discussed.
All the simulations performed in this part are conducted in a rectangle domain of size  , i.e., a
, i.e., a  grid. A nano-single crystal sample with hexagonal lattices (two-dimensional) is placed in the domain
grid. A nano-single crystal sample with hexagonal lattices (two-dimensional) is placed in the domain  . A small coexisting liquid boundary of width
. A small coexisting liquid boundary of width 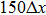 is included on both left and right sides of the sample. The reason why we use coexisting liquid at the boundaries is the requirement of solving the dynamics equation in the MPFC model efficiently. Usually, the dynamics equation is spectrally implemented in the Fourier space, thus the boundary conditions should be periodic in all directions. So, to satisfy this requirement, the free surfaces are created by choosing chemical potential to vary spatially over narrow strips near the solid–liquid interfaces of the system. This is accomplished by choosing values of r and φ0 from the coexistence region of the hexagonal solid and liquid phase diagram.[8,9] By using a lever rule, the amounts of liquid and solid in the simulated sample are set with no preference toward crystallization or melting, i.e., a stable interface arises at the boundary. Thus the sample could be considered as having periodic boundary conditions at y = 1 and y = 1024 and free boundary conditions elsewhere. Several of the following simulations require the incorporation of external loads. After the sample has equilibrated (the relaxed state in Fig. 1(a)), the atoms within the narrow strips (white line with an arrow in Fig. 1(b)) at
is included on both left and right sides of the sample. The reason why we use coexisting liquid at the boundaries is the requirement of solving the dynamics equation in the MPFC model efficiently. Usually, the dynamics equation is spectrally implemented in the Fourier space, thus the boundary conditions should be periodic in all directions. So, to satisfy this requirement, the free surfaces are created by choosing chemical potential to vary spatially over narrow strips near the solid–liquid interfaces of the system. This is accomplished by choosing values of r and φ0 from the coexistence region of the hexagonal solid and liquid phase diagram.[8,9] By using a lever rule, the amounts of liquid and solid in the simulated sample are set with no preference toward crystallization or melting, i.e., a stable interface arises at the boundary. Thus the sample could be considered as having periodic boundary conditions at y = 1 and y = 1024 and free boundary conditions elsewhere. Several of the following simulations require the incorporation of external loads. After the sample has equilibrated (the relaxed state in Fig. 1(a)), the atoms within the narrow strips (white line with an arrow in Fig. 1(b)) at 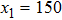 and
and  are dragged at a constant velocity
are dragged at a constant velocity 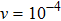 along the y-axis in opposite directions (the relaxed state in Fig. 1(b)). This is accomplished by adding an external function to the original free energy functional[26]
along the y-axis in opposite directions (the relaxed state in Fig. 1(b)). This is accomplished by adding an external function to the original free energy functional[26]
 | |
where

is the standard Gaussian function with width

and

corresponds to the analytical expression of the equilibrium
φ field (Eq. (
6)). This added free-energy term has the effect of coupling the crystalline field to another field which is translated at a velocity
v. This coupling produces an applied force which causes the lattice to translate at constant velocity ±
v.
3.1. Shear deformation responseTo demonstrate the presence of elastic relaxation modes in the MPFC model, we performed simulations of a nano-single crystal specimen as described above (the initial crystal orientation equals to zero) under shear deformation. In the PFC paradigm, the crystal atoms can be interpreted as the discrete set of maxima of the continuous density field. Figure 2(a) shows the position in the case of the row of atoms in  direction (depicted by white atoms in Fig. 1(a)) at four different strain levels. Here, the atom position was extracted by using the atomic position detection (APD) method,[27] where the locations of local maxima in the atom density field were tabulated after each time-step. When the dragged atoms are displaced by an amount D0, which is vertical to the initial
direction (depicted by white atoms in Fig. 1(a)) at four different strain levels. Here, the atom position was extracted by using the atomic position detection (APD) method,[27] where the locations of local maxima in the atom density field were tabulated after each time-step. When the dragged atoms are displaced by an amount D0, which is vertical to the initial  direction, a linear displacement distribution,
direction, a linear displacement distribution, 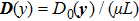 (μ is the shear modulus), will be established. The data (Fig. 2(a) with
(μ is the shear modulus), will be established. The data (Fig. 2(a) with  clearly show that the crystal response is consistent with elasticity theories, as shown by the rigid tilting of atoms in the
clearly show that the crystal response is consistent with elasticity theories, as shown by the rigid tilting of atoms in the 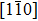 direction. At the same time, we can conclude that equation (3) can describe the elastic response in strained crystals at finite strain rates.
direction. At the same time, we can conclude that equation (3) can describe the elastic response in strained crystals at finite strain rates.
On the other side, for  , the crystal atoms fail to react fast enough to the shear deformation and the behavior is viscoelastic, as shown in Fig. 2(b). What is more, the curve fails to obey a linear displacement distribution. It means that the shear strain wave can only propagate with a limited range. In Fig. 2(c), the propagating range W of the strain wave is plotted with respect to the parameter β. When
, the crystal atoms fail to react fast enough to the shear deformation and the behavior is viscoelastic, as shown in Fig. 2(b). What is more, the curve fails to obey a linear displacement distribution. It means that the shear strain wave can only propagate with a limited range. In Fig. 2(c), the propagating range W of the strain wave is plotted with respect to the parameter β. When  , the propagating range stays constant (shown in the insert of Fig. 2(c)), which indicates that in this parameter range, the system reveals an elastic response. When
, the propagating range stays constant (shown in the insert of Fig. 2(c)), which indicates that in this parameter range, the system reveals an elastic response. When 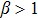 , the curve decreases dramatically. In this case, the system corresponds to very overdamped dynamics and could model the viscoelastic behavior. With the above analysis, we know that if we want to simulate the elasticity response of the system, we should choose the parameter β in elasticity regimes (
, the curve decreases dramatically. In this case, the system corresponds to very overdamped dynamics and could model the viscoelastic behavior. With the above analysis, we know that if we want to simulate the elasticity response of the system, we should choose the parameter β in elasticity regimes ( ).
).
3.2. Strain distribution in shear deformationThe purpose of this section is to demonstrate that the MPFC approach can be used to investigate the elastic strain response at atomic scales. In continuum models of a 2D lattice, distortions of the lattice can be defined by numerical differentiation[28]
where
εij describes the total strain tensor. The strains
εxx and
εyy represent the isotropic dilation (or compression) components, while
εxy is the shear component (anti-clockwise positive). In order to obtain these strain components, here we use a numerical image-processing technique named as the peak pairs analysis (PPA) to precisely determine the strain field at atomic length scales. The details of the method can be referenced to Refs. [
28] and [
29].
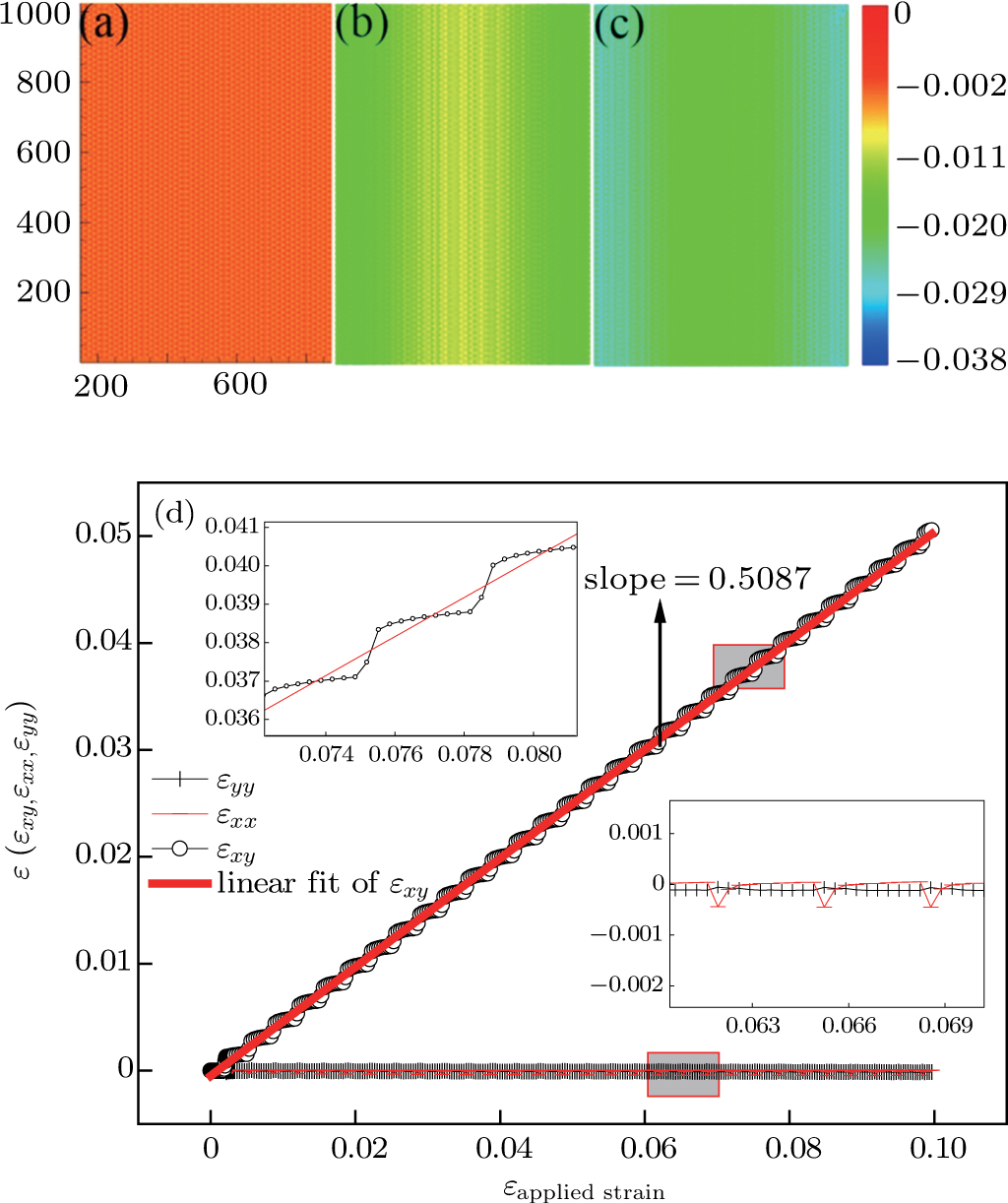
We have characterized the strain distribution for the specimen (the initial crystal orientation equals to zero) described in Fig. 2(a) in subSection 3.1. Figure 3 shows the shear strain ( distribution contours during shear deformation at four different strain levels. Figures 3(a)–3(c) reveal a gradual increase in the shear strain from the dragged atoms to the core of the specimen during deformation. This is evidenced by the gradual change in color from orange to green and to light blue. Finally, there is an almost homogeneous distribution within the whole specimen (Fig. 3(c)), which will be confirmed in the following parts. Figure 3(d) shows the strain response to external applied strains. During the whole deformation process, the values of εxx and εyy can be considered to be almost zero, and εxy is a linear function of the applied strain. According to the linear elastic theory, the theoretical value of the applied shear strain (engineering) is twice of shear strain εxy. The corresponding simulated result is
distribution contours during shear deformation at four different strain levels. Figures 3(a)–3(c) reveal a gradual increase in the shear strain from the dragged atoms to the core of the specimen during deformation. This is evidenced by the gradual change in color from orange to green and to light blue. Finally, there is an almost homogeneous distribution within the whole specimen (Fig. 3(c)), which will be confirmed in the following parts. Figure 3(d) shows the strain response to external applied strains. During the whole deformation process, the values of εxx and εyy can be considered to be almost zero, and εxy is a linear function of the applied strain. According to the linear elastic theory, the theoretical value of the applied shear strain (engineering) is twice of shear strain εxy. The corresponding simulated result is 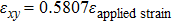 , indicating the quantitative consistency with the elastic theory.
, indicating the quantitative consistency with the elastic theory.
To illustrate the strain distributions in the local areas, the strain pattern is further examined. Figure 4(a) shows the variation of the strain extracted from the line regions, parallel to the applied shear direction at four fixed x pixels in Fig. 3(c). The shear patterns in Fig. 4(a) are approximately linear, which means that the strain wave propagates with the same velocity along the x direction. In contrast, figure 4(b) shows the same variation of strain but the line regions vertical to the applied shear direction at four fixed y pixels in Fig. 3(c). We can note that all the curves (Fig. 4(b)) are close to a symmetric distribution with the minimum strain value at the center and with the maximum value near the dragged atoms, with  (
( is defined as the strain concentration), the value is in excellent agreement with the previous analysis results,[30] in which the value is 1.8. To illustrate the strain distributions in the whole area of the specimen, the shear strain evolving distribution histograms are further examined (Figs. 4(c)–4(e)). These histograms are gained through counting the strains of all the atoms in the specimen (Fig. 3(c)). From Figs. 4(c)–4(e), we can see that the Gaussian profile matches the strain distribution extremely well without regard to those atoms with a strain value very near zero. Furthermore, the widths of the strain distributions are almost the same. Thus we can confirm that the strain distribution in the specimen interior is extremely uniform during the whole stage of deformation.
is defined as the strain concentration), the value is in excellent agreement with the previous analysis results,[30] in which the value is 1.8. To illustrate the strain distributions in the whole area of the specimen, the shear strain evolving distribution histograms are further examined (Figs. 4(c)–4(e)). These histograms are gained through counting the strains of all the atoms in the specimen (Fig. 3(c)). From Figs. 4(c)–4(e), we can see that the Gaussian profile matches the strain distribution extremely well without regard to those atoms with a strain value very near zero. Furthermore, the widths of the strain distributions are almost the same. Thus we can confirm that the strain distribution in the specimen interior is extremely uniform during the whole stage of deformation.
3.3. Orientation dependence of the shear modulusThe magnitude of the material’s elastic anisotropy plays an important role in elastic interactions. Here we show how anisotropy enters into the model. The shear modulus of the hexagonal crystal can be obtained by calculating the energy costs for deforming the equilibrium state. First, we can consider perturbations of the density field in an equilibrium state (Eq. (6)), i.e.,
In such calculation,
ξ represents the dimensionless strain. According to Wu’s work,
[31] for small strains, we can set the
q value equal to the wave number of the unstrained state, and assume the amplitude
A is the same for simplicity. To determine the elastic energy, we substitute Eq. (
19) into the free energy functional of Eq. (
1), which can be explicitly evaluated in terms of
A,
q, and
ξ. Then minimizing the resulting free energy with respect to
ξ yields
where

. To the lowest order in
ξ, the elastic energy density can be expressed as
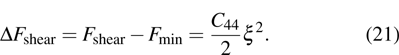 | |
The elastic constants are then  and the shear modulus
and the shear modulus  . But the above analytical calculation has not considered the orientation dependence of the shear modulus. Characterizing the modulus of the hexagonal crystal needs two variants, the shear constant C44 and an orientation factor, as a function of θ, where the angle is defined between the
. But the above analytical calculation has not considered the orientation dependence of the shear modulus. Characterizing the modulus of the hexagonal crystal needs two variants, the shear constant C44 and an orientation factor, as a function of θ, where the angle is defined between the 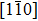 crystal direction and the directions of x-axis (perpendicular to the loading direction). For the purpose of coupling the density field and the crystal orientation, we need to start the calculation from the model. First choose two basic reciprocal lattice vectors (
crystal direction and the directions of x-axis (perpendicular to the loading direction). For the purpose of coupling the density field and the crystal orientation, we need to start the calculation from the model. First choose two basic reciprocal lattice vectors (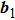 and
and 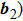 with the magnitude described in Eq. (5), and a coordinate rotation maps the two variables into new variables (
with the magnitude described in Eq. (5), and a coordinate rotation maps the two variables into new variables ( and
and 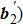 so as to determine the directions. The coordinate rotation can be described as
so as to determine the directions. The coordinate rotation can be described as  (j = 1,2). Then the density field containing crystal orientation can be obtained as
(j = 1,2). Then the density field containing crystal orientation can be obtained as  . To obtain the elastic energy density, we substitute
. To obtain the elastic energy density, we substitute  into the free energy functional (Eq. (1)) and again use the same procedure described in Eqs. (1), (9), and (11).
into the free energy functional (Eq. (1)) and again use the same procedure described in Eqs. (1), (9), and (11).
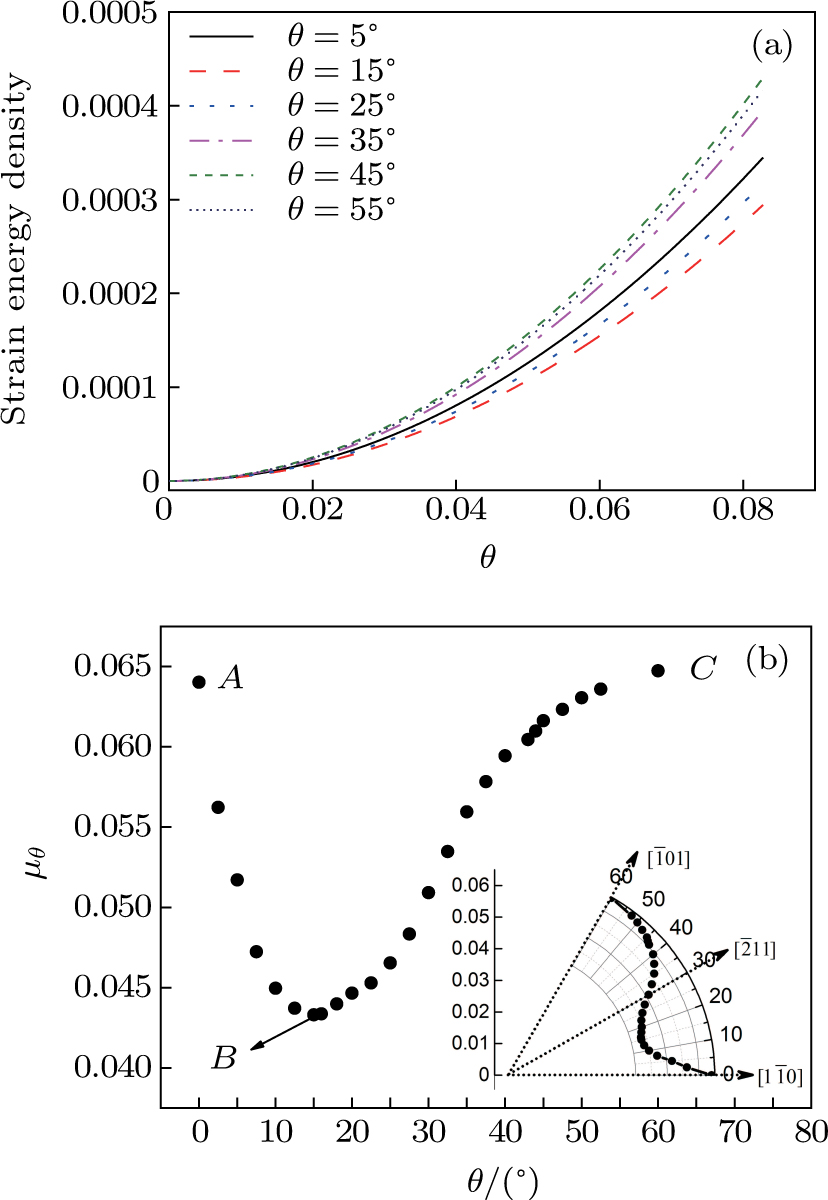
We have given a general analysis procedure for calculating the orientation dependence of the shear modulus. Since the analytical calculation is too cumbersome when adding the crystal direction angle θ to the free energy functional, here we focus only on the numerical approach to investigate how the angle θ influences the shear modulus. To accomplish this, we repeat the similar simulation in subSection 3.2 with the same domain size and the same related parameters. The only difference is that the nano-single crystal specimens are sheared with different initial crystal orientations. Figure 5(a) shows the calculated elastic energy with different orientation angles. The energy change trends are consistent in all situations and strictly fitted to the quadratic form of Eq. (21), where the shear constant C44 is easily extracted. Figure 5(b) shows the orientation dependence of shear modulus (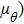 . Due to the symmetry of the hexagonal structure, when the angle θ equals to zero or 60°,
. Due to the symmetry of the hexagonal structure, when the angle θ equals to zero or 60°,  reaches the maximum at the same time shown as points A and C in Fig. 5(b), which correspond to the
reaches the maximum at the same time shown as points A and C in Fig. 5(b), which correspond to the  and
and  directions, respectively (shown in the inset). However, when the shear direction in not parallel to the main crystal direction, at the angle θ of about 15°,
directions, respectively (shown in the inset). However, when the shear direction in not parallel to the main crystal direction, at the angle θ of about 15°,  reaches the minimum (point B in Fig. 5(b)). Traversing from the whole curve, we can find that the shear modulus reflects the high anisotropy.
reaches the minimum (point B in Fig. 5(b)). Traversing from the whole curve, we can find that the shear modulus reflects the high anisotropy.
3.4. Temperature dependence of the shear modulusIn this part, we show the dependencies between the temperature r and the shear modulus μr. The effective temperature r modulates the magnitude of the amplitude of the hexagonal crystal, which changes the shear modulus. In subSection 3.3, we have obtained the relationship  , where
, where
Thus the analytic solutions can be easily obtained. What is more, for the numerical solutions, we also repeat the similar simulation in subSection
3.2 with the same domain size and the related parameters. The only difference is that the specimens are sheared with different initial temperatures. Figure
6 shows the calculated elastic energy with different temperatures. The energy change is also fitted to the quadratic form of Eq. (
21). The upper left inset of Fig.
6(a) shows the enlarged images of the region enclosed in the red shadow box, which shows that although the differences between these curves are very close to each other, it can make a big difference in the magnitude of the shear modulus. Figure
6(b) compares the analytic and numerical solutions of shear modulus
μr for a variety of values of
r. The results show that the numerical solutions of
μr decrease linearly with increasing temperature (red solid line). For the analytic solutions, it is quite close to the numerical solutions and becomes exact when the absolute value of
r is small enough, but a deviation from the numerical solutions occurs when the system temperature falls below a certain value at
r = −0.665. This deviation can be attributed to the hexagonal lattice contraction due to the nonlinear coupling of the principle reciprocal lattice vectors to higher order reciprocal lattice vectors.
[31] Thus the analytic results can in principle be systematically improved by including higher orders in the expansion of the density field.