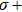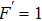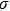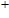† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 51275523), the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20134307110009), the Graduate Innovative Research Fund of Hunan Province, China (Grant No. CX20158015), and the Excellent Graduate Innovative Fund of National University of Defense Technology (NUDT) (Grant No. B150305).
We develop a simple and practical scheme to apply sideband cooling to a cloud of rubidium atoms. A sample containing 4 × 10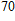
Ever since the first sub-Doppler temperatures were observed in optical molasses,[1] experimenters have pushed laser cooling techniques towards lower temperatures at higher densities. For further cooling, it is usually necessary to scatter more cooling photons, which results in spontaneous emission. These photons are on resonance with other atoms in the sample, making it optically dense. Density dependent heating is a limiting factor in laser cooling. Once a cooling photon is scattered it possesses a random polarization and propagation direction, subject to conservation of linear and angular momentum. Thus, it cannot contribute to the laser cooling effect and instead heats each atom it re-scatters by one recoil energy 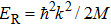
These limitations prompted the development of so-called “dark-state” cooling schemes, such as free space Raman cooling (FSRC), velocity selective stimulated Raman transitions,[8–10] blue-detuned Sisyphus cooling or “Grey Molasses”,[11,12] dark spot magneto-optical trap (MOT),[13,14] and velocity selective coherent population trapping (VSCPT).[15] However, these techniques do not use true dark states. FSRC and VSCPT are velocity selective cooling, they make use of the Doppler shift to cool atoms to specific momentum states near zero momentum, which are then dark to the cooling photons. Grey optical molasses uses polarization gradients and optical pumping to dark 
In this paper, we describe our experiments with a laser cooling technique known as Raman sideband cooling,[16–18] which is extremely insensitive to the traditional limitations of laser cooling to low temperatures at high densities. Raman sideband cooling has been successfully applied to cooling ions.[19,20] It also has been proven to work for atoms like Cs,[21] K,[22,23] and Li,[24] etc. This paper is dedicated to elucidating the mechanisms behind sideband cooling to understand how it works. In particular, we explain how it is possible to prepare a dark state with an extremely narrow linewidth, which is the key to achieving lower temperatures with laser cooling than the present experiments have allowed. Also, we develop a recipe for how to apply sideband cooling to a cloud of rubidium atoms. This technique could be used as a precooling means for the evaporation in a dipole trap, where much higher initial phase-space densities and atomic collision rates should allow the Bose–Einstein condensates to produce in a time shorter than in conventional experiments.
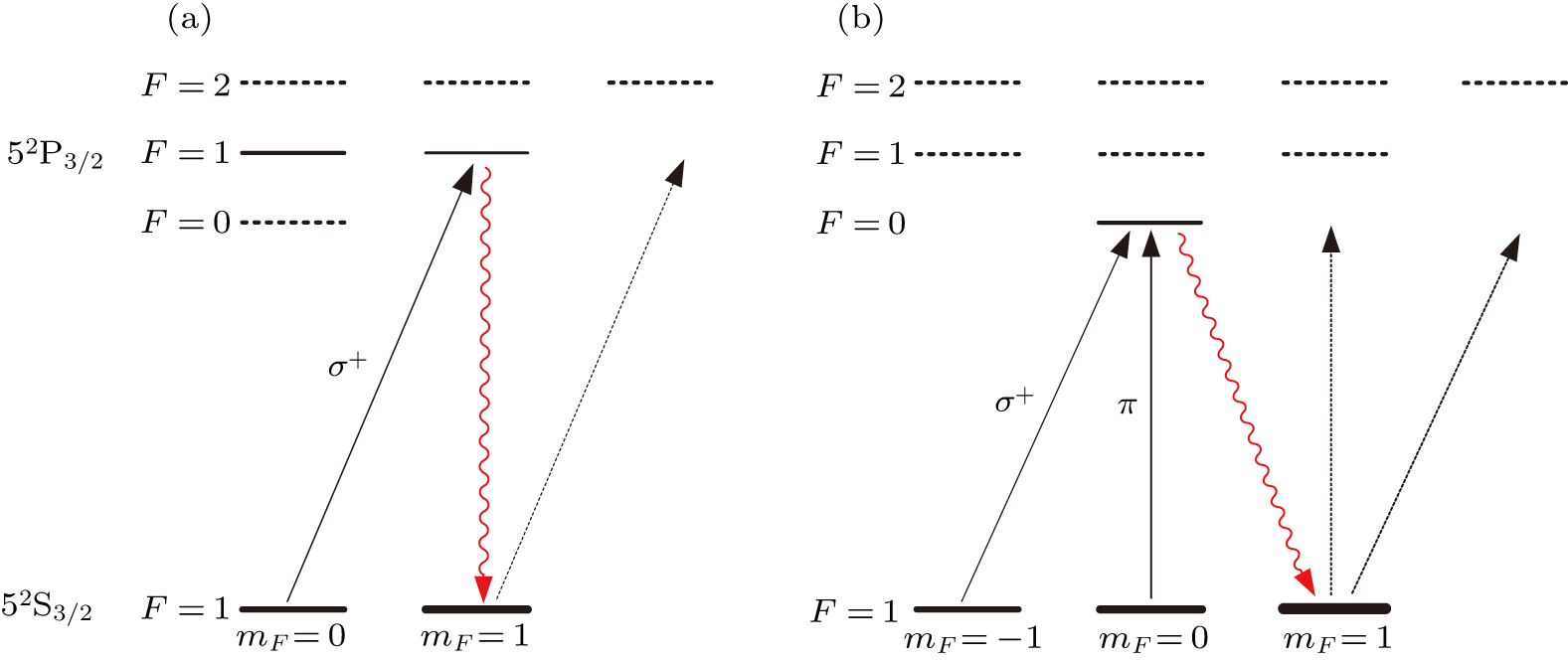
To develop a Raman sideband cooling scheme for rubidium we must choose and use a particular set of states. This choice determines the laser frequencies needed, takes into consideration the optical pumping and magnetic field. The energy level diagram for 


The dark state must be the high-field seeking 


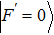


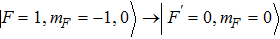

The Raman sideband cooling sequence proceeds as follows. First, a sample of 
In the absence of a magnetic field the different 




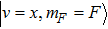

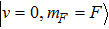
Once these levels are degenerate, 2-photon degenerate Raman transitions allow coupling between them. The photons driving this coupling can come from an external light field, however for a lattice to be tuned close to resonance (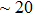
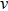


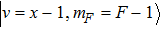
This symmetry is broken by introducing state-dependent optical pumping. Optical pumping is arguably the most important part in the sideband cooling, as it is the key to cooling. The cooling effect in the ground state 

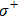



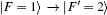


Note that the recoil energy gained from the final electronic excitation is smaller than the vibrational spacings. It is typically unable to change the vibrational levels, which allows this whole process to lower the vibrational state of the atom and cool the sample, in addition to giving the excited state an artificially long lifetime. It is also important to note that the optical pumping step is crucial and without the spontaneous emission step the atom is able to just realize the transition between states without any actual cooling occurring.
All the lasers in our system are external cavity diode lasers (ECDL), locked using saturated absorption spectroscopy (SAS). The trapping laser is amplified using a tapered amplifier (TA) to increase the power, and passes through a double pass acoustic-optic modulator (DP AOM), resulting in about 240 mW of trapping light to the glass cell. Immediately after the locking loop, a small amount of light is detuned using a DP AOM for use in imaging. This allows the imaging light to be tuned independently from the trapping light. The repump laser passes through an SAS and a single pass AOM, and the first order diffracted light is then fibre coupled to the glass cell with a total power of 12 mW. The zero order diffracted light passes through a double pass AOM and then fibre coupled to the glass cell used for optical pumping beam.
The laser used to generate the lattice is derived from an ECDL. It seeds a tapered amplifier (TA), which undergoes spatial filtering through a PM fibre before it goes to the cell. A home-built high fitness wave-meter[25] is added to easily and accurately detune the laser where we want. This allows the laser to be locked at any frequency by using a software PID and is experimentally simple to implement, as it requires only 10 μW of light coupled into the wave-meter fiber from the back of the SAS beamsplitter. In order to avoid spontaneous emission, the optical lattice is set to be 20-GHz detuning to the red of the resonance.
The intensity of the lattice is controlled directly by pulsing the current through the tapered amplifier through using a function generator (Agilent 33250A) and a Wavelength Electronics PLD5000 5A laser diode driver. This technique has been demonstrated before by Takase et al.,[26] and is useful for producing a high power output from a tapered amplifier when the limited seed light is available, or when the application only requires a large power for a short amount of time.
A polarized beam splitter is used to divide the total lattice power. Before the polarized beam goes into the cell, wave plates are placed to adjust the polarization of each lattice beam. We use three beams to build a two-dimensional (2D) lattice: a single beam retro-reflected back along its path, which passes vertically down through the cell. The third beam is held horizontally. All three beams are linearly polarized, with a 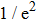
Our experiment starts with an MOT capturing approximately 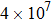


In order to realize the adiabatic loading and unloading, the lattice intensity must follow a specific functional form to avoid overheating the atoms.[27] The adiabatic loading and unloading of the lattice is demonstrated in Fig. 
The lattice loading is overlapped with the end of PGC, after that, the molasses laser beams are extinguished, leaving the atoms in the optical lattice only. The magnetic field and optical pumping beam turn on 3 ms later after the lattice beam has turned on. For the best cooling, all the parameters should be optimized. Figure 
The magnetic field, used to produce Zeeman splitting between the 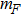
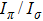
The duration of the cooling, with optical pumping and magnetic field being both on, is optimized to be 15 ms, after which the optical pumping is extinguished with an AOM in 

Taking advantage of the sideband cooling in optical lattice, the temperature cools down to around 1.5 μK from 12 μK after PGC in less than 20 ms. The cloud density after PGC is 1.6 × 10

In conclusion, we developed a simple and powerful atomic cooling method in far-detuned optical lattices that achieves much lower atomic temperature than optical molasses, and produces high phase-space density in the meantime. Sideband cooling is highlighted as a suitable replacement, allowing a larger atom number to be cooled to temperatures comparable to those obtained through RF evaporation in a magnetic trap. The ability to achieve low temperature and high phase space density within a short time opens the door for high precision measurement applications such as atomic clocks or atom interferometer, it could also be used as a precooling means before evaporation cooling to obtain BECs, and may be a promising method of achieving quantum degeneracy with purely optical means.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] |