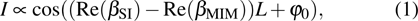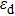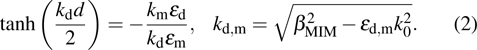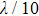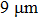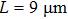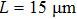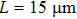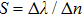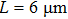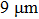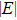Plasmonic Mach–Zehnder interferometric sensor based on a metal–insulator-metal nanostructure
Jiangsu Key Laboratory on Opto-Electronic Technology, School of Physical Science and Technology, Nanjing Normal University, Nanjing 210023, China
† Corresponding author. E-mail:
wangming@njnu.edu.cn
1. IntroductionSince Ebbesen reported on extraordinary optical transmission (EOT) in 1998, metallic nanostructures have been the focus of intense research due to their unique optical properties.[1–5] Surface plasmon polaritons (SPPs), electromagnetic waves propagating along dielectric–metal interfaces,[6,7] have tight field confinements and large enhancement effects of localized fields. As a result, they are quite sensitive to the index variations of the nearby or surrounding dielectric medium. This attractive property of SPPs is the basis for surface plasmon resonance (SPR) biosensing, which typically uses prisms to couple light into a single surface plasmon mode on a flat, continuous metal film in the Kretschmann configuration.[8] While this approach has a sensitive detection capability, the intrinsic size and alignment requirements of prism-based SPR sensors are a significant limitation for applications requiring integrated, low-cost, compact devices for portable, and rapid bioanalytical measurements.[9–12] Nanoplasmonic sensors employing nanoparticles or nanostructured metallic films to couple the incident light directly into SPPs are an emerging sensing platform that can help overcome the above limitations.[10–13] They permit low-cost, miniaturized biosensing and the potential for high-multiplexing detection without requiring a bulky and complex prism-coupling configuration. Various nanoplasmonic structures have been successfully applied to novel biosensing applications, including catalytic reaction probes,[14] molecular vibrational spectroscopy,[15] enhanced detection of chiral molecules,[16] and live viruses detection.[17] However, the relatively low sensitivities and large detection limits of nanoplasmonic sensors reported are drawbacks that must be addressed.
Surface plasmon interferometry has recently been suggested as a promising new technique for ultrasensitive plasmonic biosensing. By tailoring the nanostructure as well as the amplitude and phase of propagating SPPs in two interfering channels, one can effectively engineer the line shapes, providing new opportunities to improve sensor performance.[18–22] In our previous report,[23] a plasmonic interferometer consisting of a central aperture surrounded by two semicircular nanogrooves patterned on a gold film has been demonstrated. While this proposed structure has advantages of high contrast, simple structure, and compact dimension, its sensitivity still needs to be increased.
In this work, we propose a compact plasmonic Mach–Zehnder interferometer (MZI) for sensitive and multiplexed sensing. This simple interferometric sensor consists of a semicircular aperture-slit nanostructure patterned on a multi-layered film. The semicircular slit scatters a normally incident light beam into multi-frequency SPPs propagating at the metal/dielectric interface and in the metal–insulator–metal (MIM) waveguide, respectively, leading to an interference at the aperture in the far-field scattering. The finite-difference time-domain (FDTD) method is employed to verify the proposed design. The simulation results illustrate that our scheme provides tunability for sensing capability. Furthermore, the structure proposed in this work has the advantages of improved sensitivity, simple design, and compact dimension.
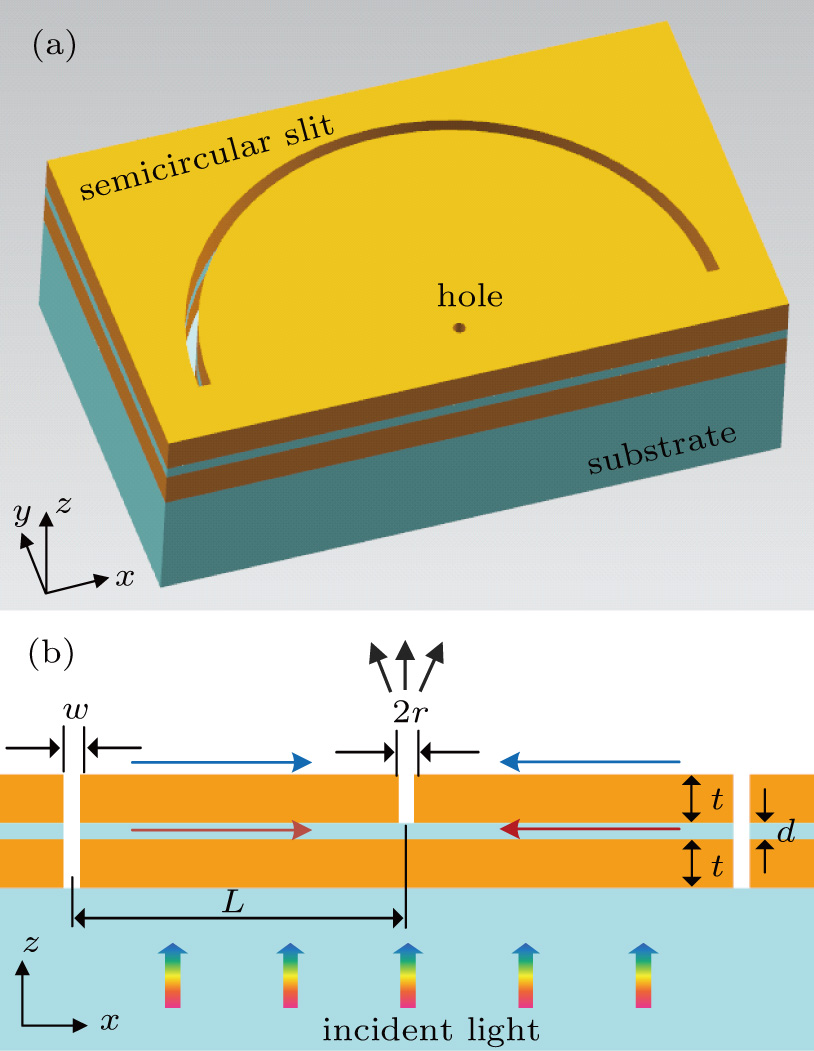
2. Structure design and simulation methodThe proposed plasmonic MIM-MZI structure is illustrated in Fig. 1(a). A three-layered MIM film (i.e., Au–SiO2–Au) is deposited on a glass substrate. The thickness t of the Au layer is 300 nm and the core SiO2 layer thickness d is 100 nm. One deep semicircular nanoslit with a width of w = 300 nm is patterned through all three layers. An aperture with a radius of r = 150 nm is patterned through the first metal film only.
As shown in Fig. 1(b), the sensing arm of this MZI design is the top Au/dielectric interface supporting single interface SPPs (SI-SPPs). The reference arm is the core SiO2 layer sandwiched by two Au films, supporting MIM-SPPs. When the semicircular nanoslit is illuminated by a collimated light beam from the glass substrate side, it scatters part of the incident radiation into SI-SPPs (sensing arm) and MIM-SPPs (reference arm), respectively. These two SPP modes propagate along the light paths and will be scattered by the central aperture, leading to an interference in the far-field transmission. This plasmonic MZI design prevents the sensing arm from being illuminated by the incident light, hence releasing the two SPP modes interference requirement. The main difference between this structure and the previously reported single-layered MZI design[19,24,25] is that the reference arm is now a MIM-waveguide rather than a flat metal/glass interface. For this case, the resulting total interference intensity can be described as follows:
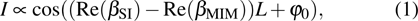 | |
where
L is the arm length of the interferometer (i.e., radius of the semicircular nanoslit).

and

represent the real parts of the propagating constants of SI-SPP and MIM-SPP, respectively.
φ0 is an additional constant phase difference between the two SPPs due to coupling and scattering processes. The propagation constant for the SI-SPP mode is given by

, where

and
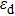
are permitivities of metal and dielectric materials on the top interface, respectively. The propagation constant for the MIM-SPP mode can be calculated by
[26,27]
Here
d is the width of the MIM waveguide and

is the light propagation constant in a vacuum.
To examine the interplay between the multiple geometric parameters and the device characteristics, the FDTD commercial software package (Lumerical Solution Inc.) is adopted in our numerical analyses. In the FDTD three-dimensional (3D) calculations, the plane wave is normally incident from the back substrate and polarized along the y-axis. Perfectly matched layers (PML) boundary conditions are applied in all directions of the simulation domain. Automatic nonuniform conformal mesh technology is used for the simulation considering the size of the proposed model, and the grid size is set to 5 nm for the aperture region. Theoretically, the calculation result is acceptable as long as the mesh size is less than 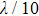 . The optical response of gold is modeled through the fitting of experimental data by multi-coefficient models.[28]
. The optical response of gold is modeled through the fitting of experimental data by multi-coefficient models.[28]
3. Results and discussion3.1. Dependence of interference spectra of the MIM-MZI on arm lengthWith the FDTD-based method, the spectra of the proposed interferometer with varied arm lengths (L) are simulated. The refractive index of the dielectric is 1.331. Figure 2(a) shows a simulated color map of light intensity at the aperture of a series of plasmonic interferometers with varying L (6–15  , in steps of 50 nm) as a function of wavelength (600–1000 nm). This color map is constructed by stacking spectra (vertical black box in Fig. 2) of plasmonic MIM-MZIs according to increasing L. It is obvious that the color of each point in the map corresponds to the simulated interference intensity for an interferometer with a specific arm length and wavelength. It is found that as the arm length L increases, the maximum amplitude of the light intensity gets enhanced. The increase results from the larger L causes more excitation of SPPs from the semicircular slit. With larger L, there are more peaks and valleys in the spectra (vertical cuts), which leads to smaller full width at half maxima (FWHM). As shown in Fig. 2(b), several simulated interference spectra are demonstrated for MIM-MZIs with arm length L of
, in steps of 50 nm) as a function of wavelength (600–1000 nm). This color map is constructed by stacking spectra (vertical black box in Fig. 2) of plasmonic MIM-MZIs according to increasing L. It is obvious that the color of each point in the map corresponds to the simulated interference intensity for an interferometer with a specific arm length and wavelength. It is found that as the arm length L increases, the maximum amplitude of the light intensity gets enhanced. The increase results from the larger L causes more excitation of SPPs from the semicircular slit. With larger L, there are more peaks and valleys in the spectra (vertical cuts), which leads to smaller full width at half maxima (FWHM). As shown in Fig. 2(b), several simulated interference spectra are demonstrated for MIM-MZIs with arm length L of  ,
, 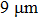 ,
,  , and
, and  , respectively. The light intensity detected at the aperture can be enhanced or suppressed depending on the incident wavelength. It is noticed that the vertical cut in Fig. 2(a) corresponds to interference spectra for the interferometer with arm length
, respectively. The light intensity detected at the aperture can be enhanced or suppressed depending on the incident wavelength. It is noticed that the vertical cut in Fig. 2(a) corresponds to interference spectra for the interferometer with arm length 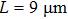 . Figure 2(c) shows an intensity profile as a function of arm length L, for a given incident wavelength (for example at 823.9 nm, as indicated by the horizontal black box in Fig. 2(a)). By setting λ to constant in Eq. (2) and using Eq. (1), we can calculate the oscillation period to be 1800.6 nm, agreeing reasonably well with the simulated result of 1800 nm shown in Fig. 2(c). This demonstrates the operating principle of the proposed device.
. Figure 2(c) shows an intensity profile as a function of arm length L, for a given incident wavelength (for example at 823.9 nm, as indicated by the horizontal black box in Fig. 2(a)). By setting λ to constant in Eq. (2) and using Eq. (1), we can calculate the oscillation period to be 1800.6 nm, agreeing reasonably well with the simulated result of 1800 nm shown in Fig. 2(c). This demonstrates the operating principle of the proposed device.
3.2. Influence of core layer thickness on interference spectraFigure 3(a) shows interference spectra of the plasmonic interferometer with different core layer thicknesses and arm length 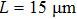 is chosen here. It is known that an MIM waveguide is able to support multiple optical modes depending on its core layer thickness. As shown in the simulation results, for the interferometers with core layer thicknesses of 100 nm, 150 nm, and 200 nm, the interference spectra exhibit different phase and intensity properties. It is found that the spectrum for the thickness of 200 nm shows amplitude fluctuation at the long wavelength location. Multi-modes will be allowed in the MIM waveguide as the thickness increases, leading to multiple interferences involving different orders of MIM-SPPs and SI-SPPs in this design. Therefore, we select a d of 100 nm to support interference between SI-SPP and the TM0 mode to obtain clear spectral interference patterns.
is chosen here. It is known that an MIM waveguide is able to support multiple optical modes depending on its core layer thickness. As shown in the simulation results, for the interferometers with core layer thicknesses of 100 nm, 150 nm, and 200 nm, the interference spectra exhibit different phase and intensity properties. It is found that the spectrum for the thickness of 200 nm shows amplitude fluctuation at the long wavelength location. Multi-modes will be allowed in the MIM waveguide as the thickness increases, leading to multiple interferences involving different orders of MIM-SPPs and SI-SPPs in this design. Therefore, we select a d of 100 nm to support interference between SI-SPP and the TM0 mode to obtain clear spectral interference patterns.
The calculated electric field distributions at the interference peak and valley wavelengths for d = 100 nm and  are shown in Fig. 3(b). Good light enhancement and light cancellation can be clearly visualized at the central aperture location, which correspond to the constructive and destructive interferences, respectively. The calculated field distributions of
are shown in Fig. 3(b). Good light enhancement and light cancellation can be clearly visualized at the central aperture location, which correspond to the constructive and destructive interferences, respectively. The calculated field distributions of  and
and  components are also shown in Fig. 3(b). It is worth noticing that the
components are also shown in Fig. 3(b). It is worth noticing that the  component plays a main role in determining the enhanced light transmission and suppression through the interferometers.
component plays a main role in determining the enhanced light transmission and suppression through the interferometers.
In order to further understand the characteristics of the proposed plasmonic interferometer, a similar design with full circle nanoslit is also simulated to make a comparison. The two samples are both set with arm length 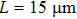 and d = 100 nm. As shown in Fig. 4, though the plasmonic interferometer with full circle nanoslit can generate more SPPs, the model we proposed has effectively decreased the cross-talk caused by the structural symmetry, providing promising potential for refractive index sensing. Also, the semicircular slit and aperture cannot be concentrically formed. As shown in Fig. 5(a), D is defined as the offset distance between the center of the semicircular slit and the hole. Figure 5(b) shows the simulated spectra for MZI designs with centrifugal distances of 0, 500 nm, and 1000 nm. It is found that the interference pattern of the plasmonic structure blue-shifts upon the increase in the centrifugal distance D, and the intensity of the transmission also gets weakened. The semicircular structure design ensures SPPs propagate radially, which allows a limited portion of SPPs to propagate towards the hole location.
and d = 100 nm. As shown in Fig. 4, though the plasmonic interferometer with full circle nanoslit can generate more SPPs, the model we proposed has effectively decreased the cross-talk caused by the structural symmetry, providing promising potential for refractive index sensing. Also, the semicircular slit and aperture cannot be concentrically formed. As shown in Fig. 5(a), D is defined as the offset distance between the center of the semicircular slit and the hole. Figure 5(b) shows the simulated spectra for MZI designs with centrifugal distances of 0, 500 nm, and 1000 nm. It is found that the interference pattern of the plasmonic structure blue-shifts upon the increase in the centrifugal distance D, and the intensity of the transmission also gets weakened. The semicircular structure design ensures SPPs propagate radially, which allows a limited portion of SPPs to propagate towards the hole location.
3.3. Sensing propertiesAccording to the working principle of the proposed structure, a change in refractive index occurring on the sensing arm can cause a spectral shift of the interference pattern, providing the basis of the sensing scheme. The sensitivity  of the plasmonic sensors is determined by
of the plasmonic sensors is determined by 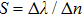 , where
, where  is the spectral shift of the peak wavelength resulted from a refractive index change
is the spectral shift of the peak wavelength resulted from a refractive index change  of the sample surrounding the nanostructure. In this context, to explore the performance of the plasmonic interferometer, we calculate the interference patterns of the structure with d = 100 nm and
of the sample surrounding the nanostructure. In this context, to explore the performance of the plasmonic interferometer, we calculate the interference patterns of the structure with d = 100 nm and  , when n changes from 1.331 to 1.352. As shown in Fig. 6(a), the interference pattern blue shifts as the refractive index increases, and the intensity also gets strengthened or weakened at different peak positions. The peak wavelengths of peak 1 (at around 831.2 nm) and peak 2 (at around 910 nm) are measured as a function of the refractive index and plotted in Fig. 6(b). One can see that the positions of the peaks vary approximately linearly with the refractive index of the surrounding environment. The sensitivities are estimated to be 1055.6 nm/RIU and 1313.4 nm/RIU for peak 1 and peak 2, respectively. It is a unique advantage of this interferometric sensor that the signal changes occur over a broad spectral range. The figure of merit
, when n changes from 1.331 to 1.352. As shown in Fig. 6(a), the interference pattern blue shifts as the refractive index increases, and the intensity also gets strengthened or weakened at different peak positions. The peak wavelengths of peak 1 (at around 831.2 nm) and peak 2 (at around 910 nm) are measured as a function of the refractive index and plotted in Fig. 6(b). One can see that the positions of the peaks vary approximately linearly with the refractive index of the surrounding environment. The sensitivities are estimated to be 1055.6 nm/RIU and 1313.4 nm/RIU for peak 1 and peak 2, respectively. It is a unique advantage of this interferometric sensor that the signal changes occur over a broad spectral range. The figure of merit 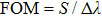 , which is defined as the refractive index sensitivity divided by the sensing peak linewidth, is estimated to be 33.3. To explore this sensor’s property for sensing schemes that require intensity interrogation, we use the figure of merit FOM* to evaluate the performance of the proposed structure, which is defined as[29]
, which is defined as the refractive index sensitivity divided by the sensing peak linewidth, is estimated to be 33.3. To explore this sensor’s property for sensing schemes that require intensity interrogation, we use the figure of merit FOM* to evaluate the performance of the proposed structure, which is defined as[29]
 | |
Here,

is the light intensity change of a fixed wavelength, and
I0 is the reference intensity of the sensor in water. As shown in Fig.
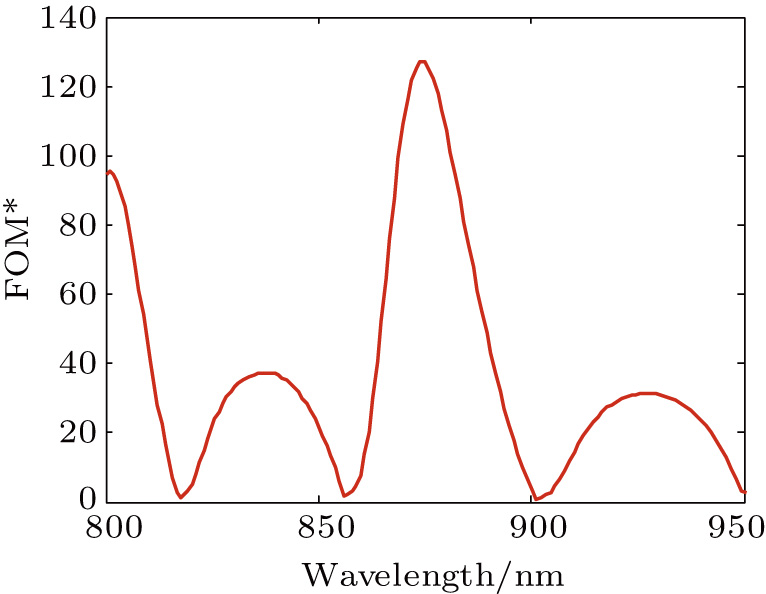
7, FOM
* can reach 127.2 at a wavelength of 873.9 nm. According to these parameters for evaluating the performance of the nanoplasmonic sensor, the proposed design has improved the sensitivity and exhibits a good sensing ability for potential applications.
4. ConclusionWe have proposed a novel plasmonic MIM-MZI based on light interference between SI-SPP and MIM-SPP, using a simple semicircular slit-aperture design. We have demonstrated the working principle both theoretically and numerically. According to the simulation results, the proposed design exhibits good tunability by changing the arm length and core layer thickness. The interference spectra show both phase and amplitude change as the refractive index changes. This design demonstrates good sensing properties, and will enable the development of low-cost, multiplexed, and compact plasmonic sensor for biosensing devices and portable optical applications.