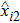† Corresponding author. E-mail:
We investigate the tracking control for a class of nonlinear heterogeneous leader–follower multi-agent systems (MAS) with unknown external disturbances. Firstly, the neighbor-based distributed finite-time observers are proposed for the followers to estimate the position and velocity of the leader. Then, two novel distributed adaptive control laws are designed by means of linear sliding mode (LSM) as well as nonsingular terminal sliding mode (NTSM), respectively. One can prove that the tracking consensus can be achieved asymptotically under LSM and the tracking error can converge to a quite small neighborhood of the origin in finite time by NTSM in spite of uncertainties and disturbances. Finally, a simulation example is given to verify the effectiveness of the obtained theoretical results.
With the development of communication networks and powerful embedded systems, distributed cooperative control for multi-agent systems (MAS) has received compelling attention from various research fields, such as robotic teams,[1] sensor networks,[2] and underwater vehicles.[3] The uncertainty and unpredictability of multi-agent systems often appear in practical applications. In the stability analysis of MAS with uncertainties, it is extremely challenging to construct the Lyapunov function properly.
Among collective behaviors of multiple agents, consensus is one of the most important behaviors, which means that all agents will reach a common state eventually. Recently, the consensus problem of multi-agent systems has been intensively studied.[4–10] In Refs. [6–8], the studies of MAS focus on linear systems. The consensus of nonlinear MAS is more challenging than that of linear MAS. Nonlinearity is ubiquitous in physical phenomena, however only a few works have been done to research the consensus of nonlinear MAS.[9–11] For example, Ren et al. studied the tracking control of second-order nonlinear MAS via two different kinds of sliding mode structures, whereas the considered model is without disturbance.[11] In practical implementations, the external disturbance may not be ignored and should be considered. In Refs. [12–21], the consensus problem of MAS with disturbances was discussed. Yang et al.[12] proposed the asymptotic convergence protocol of MAS with disturbances and some similar results can be found in Refs. [13] and [14] and the references therein. So far, most of the existing control algorithms for MAS are asymptotically convergent.[12–14, 22–24] Compared to the asymptotic consensus, the finite-time consensus control is an effective approach with high performance, good robustness to uncertainties, and better disturbances rejection properties. Zhang et al.[15] investigated the finite-time tracking control for nonlinear MAS subject to external disturbances. Chen et al.[16] solved the finite-time cooperative tracking problem for a class of networked Euler–Lagrange systems. Continuous distributed finite-time control algorithms were designed for multiple agents with double integrators in Refs. [17]. Yu et al.[18] and He et al.[19] investigated the finite-time tracking control of second-order multi-agent systems with bounded external disturbances. The former is for linear systems and the latter is for nonlinear systems. Nevertheless, the bounds of the external disturbances in Refs. [12–20, 20] are assumed to be known, which are actually difficult to obtain in practice. To estimate the unknown bounds, the adaptive control is a good method.[25, 26] Zhao et al.[25, 26] studied the attitude synchronization control problem for a group of spacecrafts and the containment control problem for second-order multi-agent systems using the sliding mode associated with adaptive methodology. At present, however, there are few results focusing on the finite-time distributed adaptive control problem for heterogeneous nonlinear multi-agent systems with unknown external disturbances.
From the review of the existing works on consensus of MAS, it can be observed that there are still some challenging issues to be addressed. One of the issues is to consider more general nonlinear MAS with heterogeneous dynamics and external disturbances. The bounds of the external disturbances may be unknown, which is more practical and challenging. Another issue is to develop more efficient control algorithms, which have the following features: 1) distributed, which means each agent can only use the local information of its neighbors; 2) finite time, which makes the tracking error converge in finite time, 3) adaptive, which can estimate the unknown bounds of the external disturbances. However, the control mechanisms in most existing results only have some but not all of these features.
Motivated by the above discussion, in this paper, we investigate the distributed adaptive sliding mode control for tracking consensus of heterogeneous second-order nonlinear multi-agent systems with unknown external disturbances. The contributions of this paper are three-fold. 1) On account of the fact that the information of the position and velocity of the leader is unmeasurable, the neighbor-based distributed finite-time observers are proposed for the followers to estimate the information of the leader. 2) Two novel distributed adaptive sliding mode control strategies are designed. The asymptotic tracking is based on linear sliding mode (LSM) and the finite-time tracking is based on nonsingular terminal sliding mode (NTSM). 3) Our rigorous proof shows that the tracking error can converge to zero asymptotically by LSM or to a quite small neighborhood of the origin in finite time by NTSM in spite of uncertainties and disturbances. Therefore, the proposed control algorithms are insensitive and robust to the uncertainties and unknown external disturbances.
The rest of the paper is organized as follows. Section
For the sake of better understanding, we recall some preliminaries on graph theory, which can be referred to Ref. [27] for more details, and then formulate our problem.
In this paper, we consider a class of leader–follower multi-agent systems consisting of one leader and N followers. The topology relationship of the followers and the leader can be described by a graph 


The undirected graph 

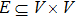
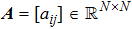

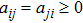


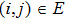

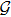



 |
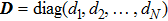
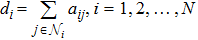
The leader adjacency matrix associated with graph 





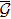

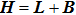
Throughout this paper, 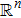



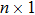



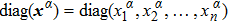
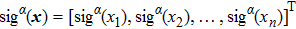


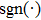

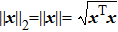




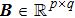
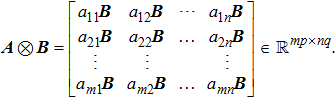 |
In this paper, the dynamics of each follower is described by the following second-order heterogeneous nonlinear MAS
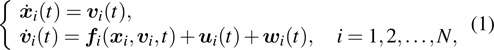 |
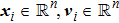
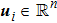
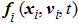
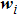
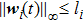
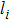
The leader’s dynamics is described as
 |
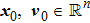
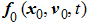
To begin with, we have the following assumptions.







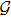


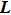

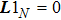




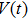
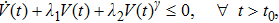 |
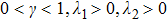
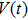
 |

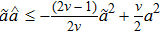

In this section, to track the leader, the control protocol 
Similar to Ref. [4], the distributed finite-time estimator is proposed as
 |
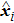
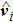
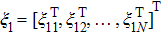
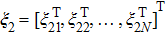
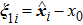
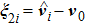

According to Eqs. (
 |

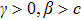





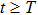
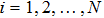
In this subsection, a new sliding mode controller protocol is proposed to guarantee that each agent can achieve the consensus as time goes to infinity.
We design the LSM vector as
 |
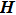

Denote 


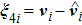

 |

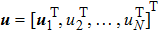

Then the LSM vector can be rewritten as
 |
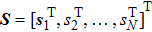
Let 
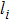

 |
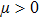
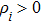
The control law based on the linear sliding mode is given as
 |
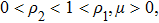
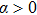
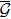






Consider the following Lyapunov function
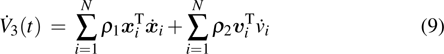 |
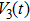
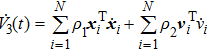 |
 |
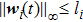
 |
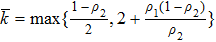
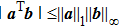
According to Assumption 1, there exists a constant 

 |
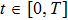
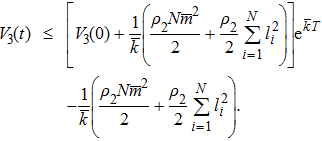 |
On the other hand, since 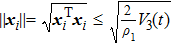



Next, when 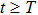
 |
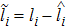
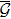
 |
From Proposition 1, we have 
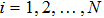

 |

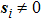
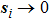
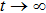
On the sliding mode 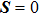
 |
 |
 |
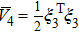
 |
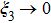

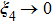
This completes the proof.
In this subsection, we come up with a novel controller based on NTSM to make the tracking error of each agent converge to a quite small neighborhood of the origin in finite time.
We design the NTSM vector as
 |
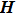
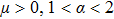
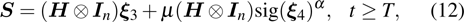 |
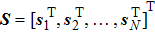
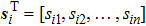
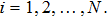
Let 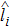
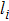

 |
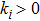
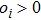
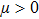
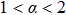
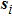

The control law based on the nonsingular terminal sliding mode is designed as
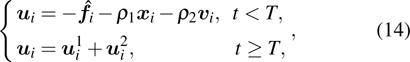 |
 |
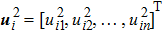
 |
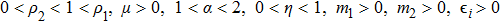
Denote 




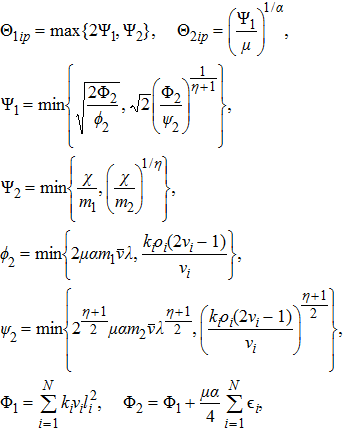 |
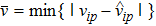
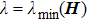
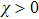
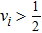


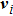

Next, when 
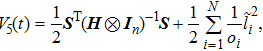 |

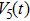
 |
(i) When 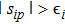
 |
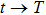
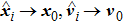

 |
 |
 |
 |
By 
 |
(ii) When 
 |
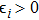
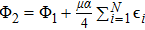
Define 


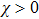
In the following, we will show that once 
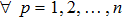
(I) For the case 
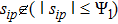
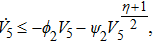 |
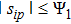
(II) For the case 

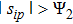
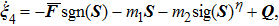 |
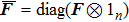
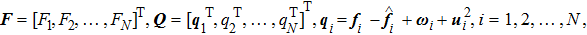
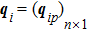
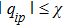
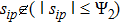
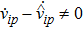
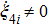
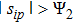
In cases (I) and (II), once 
 |
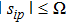
We next prove that the tracking error of MAS will converge to the region 

(III) In case (I), 


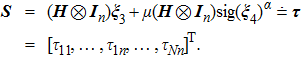 |
 |
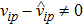
 |
 |
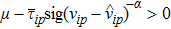
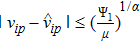
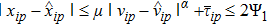
(IV) In case (II), we have 
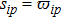


In summary, the tracking error of MAS will converge to 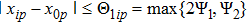


In this section, a numeral example is presented to illustrate the theoretical results. The example considers MAS (
The dynamics of the agents described in Eqs. (
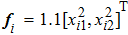



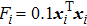


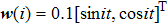
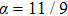
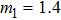







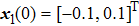





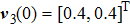

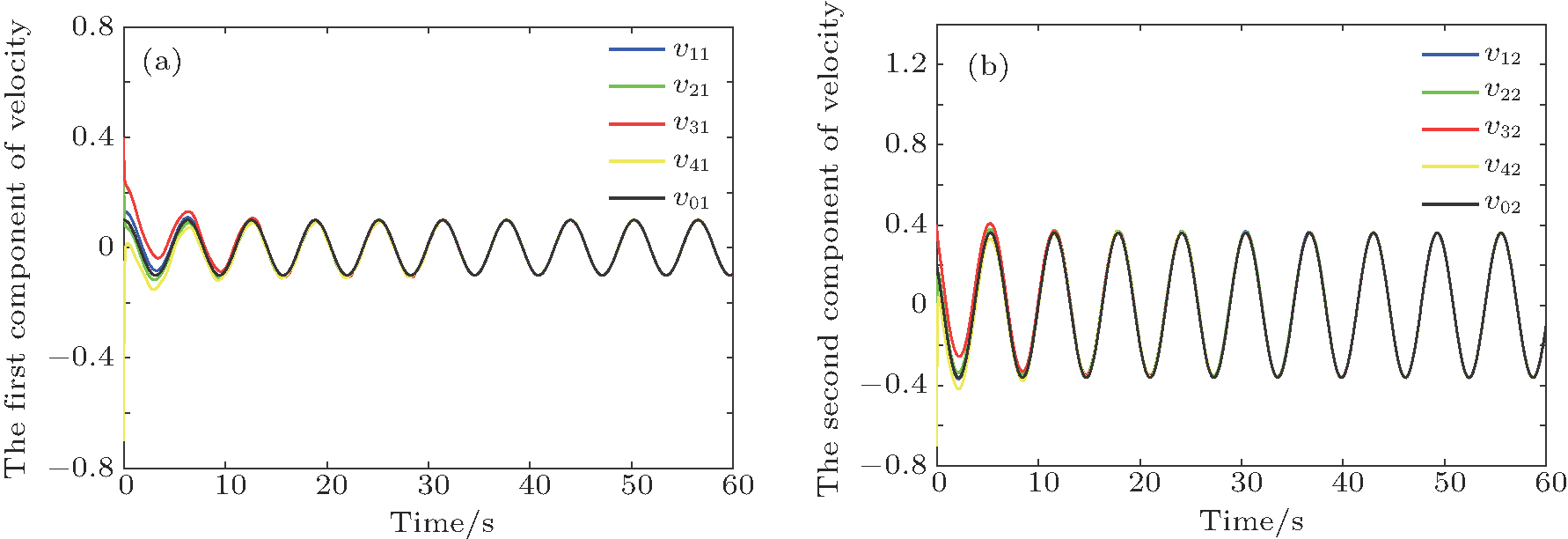
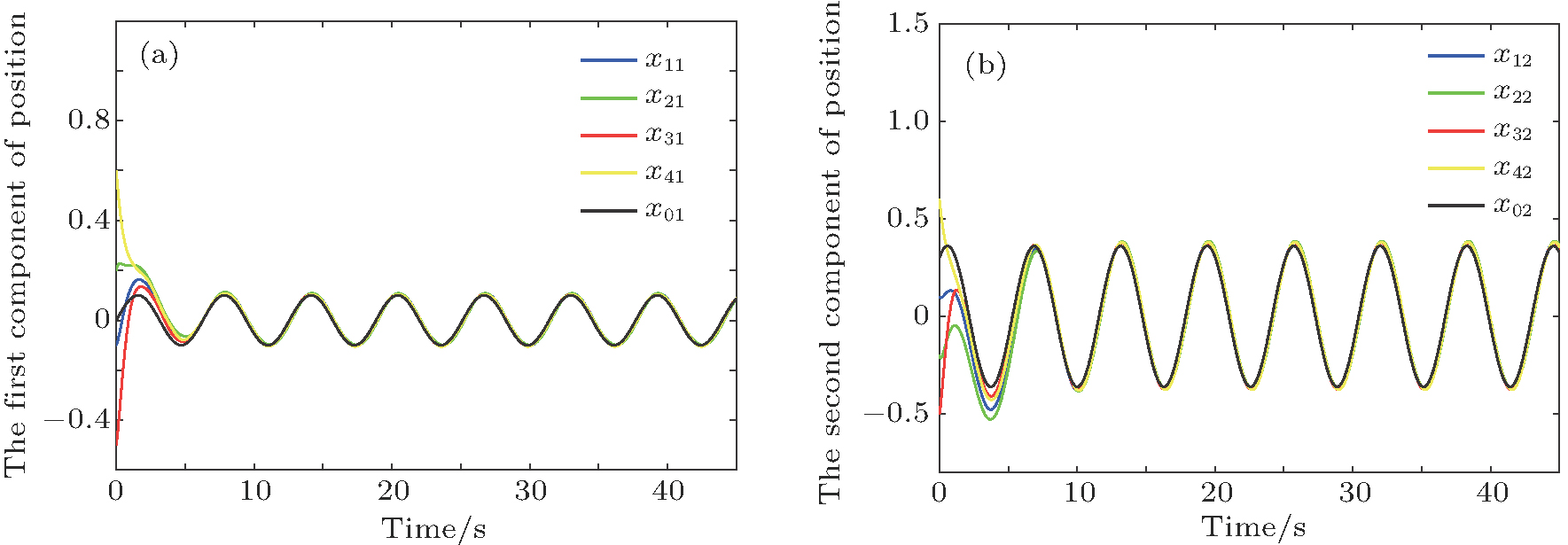
Figures 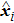
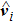
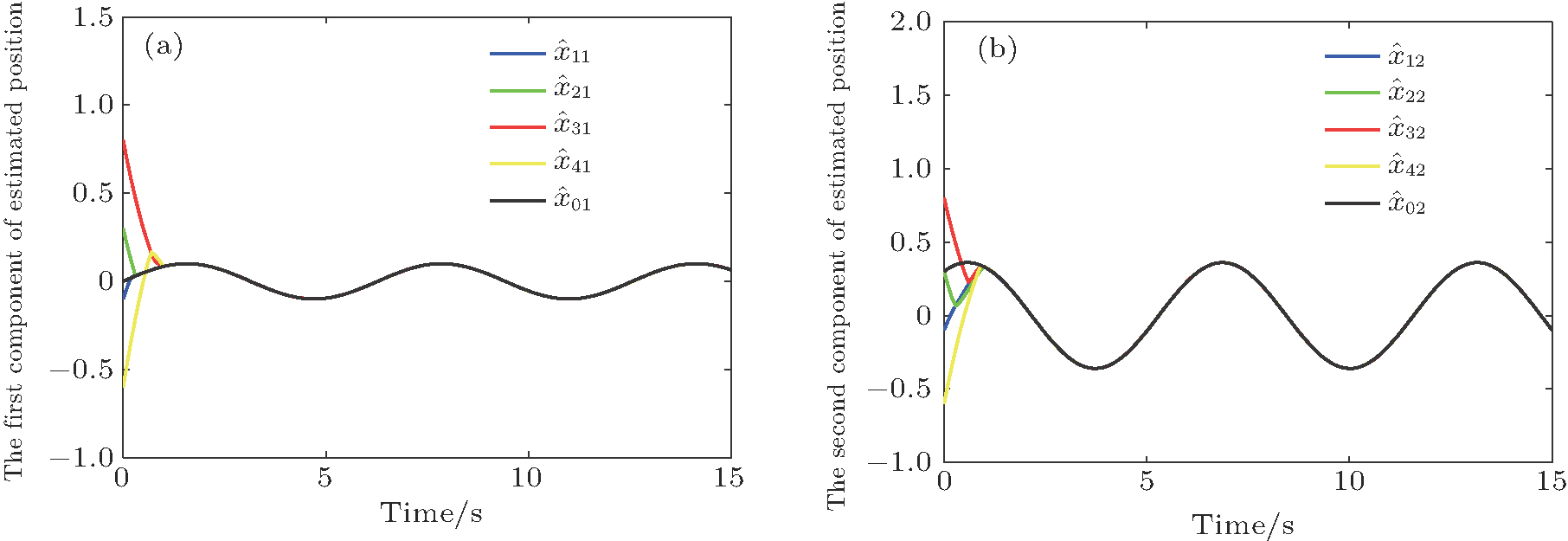 | Fig. 2. (color online) The estimated position of the i-th follower to the leader (i = 1,2,3,4): (a)   |
 | Fig. 3. (color online) The estimated velocity of the i-th follower to the leader (i = 1,2,3,4): (a)   |
We discuss the tracking control for a class of nonlinear heterogeneous leader–follower multi-agent system subject to unknown external disturbances. A second-order distributed observer is first proposed for each follower to estimate the position and velocity of the leader. Then, two new distributed adaptive control protocols based on linear sliding mode and nonsingular terminal sliding mode, respectively, are designed to guarantee the tracking errors to converge to zero asymptotically or to a quite small neighborhood of the origin in finite time. Simulations have been carried out to illustrate the validity of the main results. One of the challenging works for further research is to generalize the results to high-order multi-agent systems with uncertainties and unknown disturbances.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |