Vertical instability control in the elongated tokamak is a key design issue. Elongated plasma has a better performance than circular cross-section plasma but is inherently vertically unstable. During the vertical displacement event (VDE), the induced eddy currents interact with the magnetic field and generate large magnetic forces on passive structures. In addition, losing control of VDE leads to the plasma crashing onto the wall. Large halo currents produced magnetic forces and massive flows of particles and heat fluxes cause tremendous damage to the wall. Analysis of vertical displacement events is of great importance for tokamak plant design.

The TSC^[1] and TokSys^[2] are two widely used 2D simulation codes. They have been successfully used on several tokamaks in reproducing experimental VDE shots and/or designing vertical control systems, such as PBX,^[1] DIII-D,^[2,3] TFTR,^[4] JT-60U,^[5] EAST^[6–8] and ITER.^[9] The TSC is a full non-linear free boundary simulation code that accurately models the transport time-scale evolution of an axisymmetric plasma, including the plasma interactions with the passive and active feedback systems. The TokSys RZIP model is a linear model that treats the plasma as a fixed spatial distribution of current, and rigid radial and vertical motions are allowed. The two codes have complementary merits for each other, so their combination will be advantageous for the Chinese Fusion Engineering Test Reactor (CFETR) design. On the other hand, since the two codes differ from each other greatly, it is necessary to check out whether they can reproduce each other’s results correctly. In this study, a detailed comparison benchmark between the TSC model and the TokSys model for the VDE simulation is conducted. The focus is on the analysis of vertical instability control design for CFETR and uniform tokamak plasma parameters are used.

The CFETR is a Chinese next-step tokamak which is under engineering conceptual design. It is based on the tokamak approach with superconducting magnet technology, which is envisioned to provide 50MW–200 MW fusion power.^[10] It will be an important facility to bridge from ITER to DEMO. During the last few years, remarkable progress has been made, including the determination of the device engineering parameters,^[10] the design of the superconducting magnet system,^[11] and the remote maintenance system,^[12] and so on. The main parameters of CFETR are listed in Table 1. The geometry parameters of poloidal field coils (PF) are listed in Table 2.

Table 1.

Table 1.

Table 1. Main parameters of the CFETR. . Parameters CFETR Plasma current (Ip) 8–10 MA Toroidal field (Bt) 4.5–5 T Major radius (R0) 5.7 m Minor radius (a) 1.6 m Elongation (κ) 1.8–2.0 Plasma shape LSN

Table 1. Main parameters of the CFETR. .

Table 2.

Table 2.

Table 2. Geometric parameters of the CFETR poloidal field coils. . Coils R/m Z/m dR dZ Turns CS1U 1.415 0.999 0.650 1.938 374 CS2U 1.415 2.997 0.650 1.938 374 CS3U 1.415 4.995 0.650 1.938 374 CS1L 1.415 −0.999 0.650 1.938 374 CS2L 1.415 −2.997 0.650 1.938 374 CS3L 1.415 −4.995 0.650 1.938 374 PF1U 3.109 7.642 1.382 1.111 616 PF2U 9.400 6.698 0.909 0.909 324 PF3U 11.554 2.742 0.909 0.909 324 PF1L 3.109 −7.642 1.382 1.111 616 PF2L 9.400 −6.698 0.909 0.909 324 PF3L 11.554 −2.742 0.909 0.909 324 DC1 5.459 −7.792 0.909 0.909 324 DC2 7.640 −7.448 0.909 0.909 324

Table 2. Geometric parameters of the CFETR poloidal field coils. .

The rest of this paper is arranged as follows. In Section 2, the models of the TSC and TokSys codes for VDE simulation are compared. In Section 3, a comparison between modeling results on the CFETR vertical instability control is given including a verification of the metallic structure passive stability and a validation of the power supply requirement of an in-vessel coil control method. Finally, a summary is given in Section 4.

In TSC, in order to model a VDE process, firstly an initial equilibrium reconstruction is needed, by which the starting values are determined. In the initial equilibrium reconstruction, functional forms of pressure p(Ψ) and toroidal field function g(Ψ) are prescribed. The standard G-S function is used to iterate the poloidal flux Ψ until the convergence criterion is achieved.^[6]

After the initial equilibrium, all feedback control systems including plasma radial and vertical position control and plasma current control are shut down. A small current pulse is used to trigger the VDE. Then the plasma interacting with passive stabilizers evolves self-consistently by solving a group of complete dynamical equations describing the plasma force balance and electromagnetic evolution and transport equations.^[1]

The surrounding passive stabilizers are considered as a set of toroidal continuous filaments and the induced currents are described by poloidal flux:

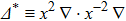
After plasma freely drifts a certain distance, the active vertical feedback control system is turned on where the vertical position of plasma current center Z_c (Ψ) is used as the control object and the applied voltage V(t) is related to Z_c through a two-layer PID controller as:

Owing to the fact that the main interest in VDE simulation is in the electromagnetic interaction between the plasma and surrounding conductors and the control of the plasma vertical position, the linearized RZIP^[13] model is used in the TokSys environment. In the RZIP model, the plasma is represented by a fixed spatial distribution of current and only rigid radial and vertical motions are allowed. Both the plasma and the surrounding conductors are represented by circuit equations:

The plasma radial and vertical positions are output as

Firstly, the passive stability of the CFETR double layer vacuum vessel (VV) is examined. The numerical model of the CFETR including VV and poloidal field (PF) coils is built in both the TSC and the TokSys. The modeling of VV contains a small difference between the two codes. In the TokSys, the size of the filament cross section is defined accurately, while in the TSC, the cross section of the filament equals the grid size that has been determined previously. Except for the above, no significant difference exists. Both codes treat the passive conductors as a group of toroidal continuous filaments with no breaks nor shunts. The equivalent resistivity of the VV is the same as that of the EAST VV model, i.e., 0.74 μΩ⋅m.^[14] The PF coils are modeled as coaxial toroidal circular loops with rectangular poloidal cross section. The sizes of PF coils are determined accurately according to the previous design.^[11]

In the TSC, in order to evaluate the VV passive stability, free drift VDE is simulated. A typical CFETR equilibrium (denoted as ‘case 1’) constructed by the EFIT^[15] code is reconstructed as the TSC initial equilibrium. Plasma shape and flux distribution are shown in Fig. 1. For the case of equilibrium construction, the comparison of parameters between the TSC and the EFIT is listed in Table 3. After the initial equilibrium reconstruction, all feedback control systems including the plasma radial and vertical position control and the plasma current control are shut down. The plasma drifts freely without control until disruption occurs. Growth time of VDE is computed to be less than 1 ms by inline fitting of the Z_c curve and listed in Table 4 (case 1).

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) Geometric model of CFETR. Contour lines denote flux surfaces of case 1 initial equilibrium reconstructed by TSC. Black thick line denotes plasma boundary computed by EFIT.

Table 3.

Table 3.

Table 3. Parameters comparison of initial equilibrium reconstruction. . Code Ip/MA κ βp li a/m Zc/m EFIT 10 2.0 0.8 1.0 1.6 0.28 TSC 10 2.0 0.8 1.0 1.55 0.28

Table 3. Parameters comparison of initial equilibrium reconstruction. .

Table 4.

Table 4.

Table 4. Comparison of VV passive stability evaluation between the TSC and the TokSys. . Equilibria Growth times/ms n/nc TSC TokSys Case 1 0.33 −1.34 −1.43 Case 2 0.45 −1.27 −1.25 Case 3 0.51 −1.24 −1.15 Case 4 0.72 −1.21 −1.11 Case 5 1.01 −1.12 −1.05

Table 4. Comparison of VV passive stability evaluation between the TSC and the TokSys. .

In the TokSys, the ratio of field decay index n/n_c is used for assessing the vertical instability controllability. The decay index n is derived from the initial equilibrium constructed by the EFIT, and the critical decay index n_c is computed by the perturbation method in which a small disturbance of the plasma current center δZ_c is assumed.^[13] The values of n/n_c are compared between the TSC and the TokSys and listed in Table 4. The results show that the TSC and the TokSys codes agree well in the sense of the evaluation of passive conductor stability.

A passive control stratagem by utilizing passive plates (PP) is tested. A pair of up–down symmetric PP is placed inside the VV as shown in Fig. 1. The EAST toroidal discontinuous PP model is used here in both codes,^[7] where the two plates are centered at R = 6.449 m and Z = ± 3.009 m and the equivalent resistivity is ∼ 1.09 μΩ⋅m. The growth rate of VDE with VV & PP passive stabilizers is computed and listed in Table 5 (case 1). The plasma evolution of case 1 including the flux surfaces and the current center Z_c is shown in Fig. 2. A comparison between results is made and the results are found to be in agreement with each other.

Table 5.

Table 5.

Table 5. Comparison of VV & PP passive stability evaluation between the TSC and the TokSys. . Equilibria Growth rates(1/s) TSC TokSys Case 1 27 25 Case 2 10 8 Case 3 6 5 Case 4 4 4 Case 5 5 5

Table 5. Comparison of VV & PP passive stability evaluation between the TSC and the TokSys. .

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) Plasma evolutions with PP & VV passive stabilizer, computed by TSC.

For confirmation of the comparison results, in total five CFETR typical equilibria with different parameters such as I_p, κ, β_p, and l_i, which are listed in Table 6, are analyzed and the results are listed in Tables 4 and 5. The results show that the TSC and the TokSys are in accord with each other in the sense of the evaluation of the electromagnetic interactions between the plasma and the surrounding conductors.

Table 6.

Table 6.

Table 6. Main parameters of the CFETR typical equilibria. . Equilibria Ip/MA κ βp li a/m Zc/m Case 1 10 2.0 0.8 1.0 1.6 0.28 Case 2 10 2.0 1.1 0.8 1.6 0.27 Case 3 10 2.0 1.3 0.7 1.6 0.26 Case 4 8 2.0 1.5 0.7 1.6 0.25 Case 5 8 1.8 1.4 1.1 1.6 0.56

Table 6. Main parameters of the CFETR typical equilibria. .

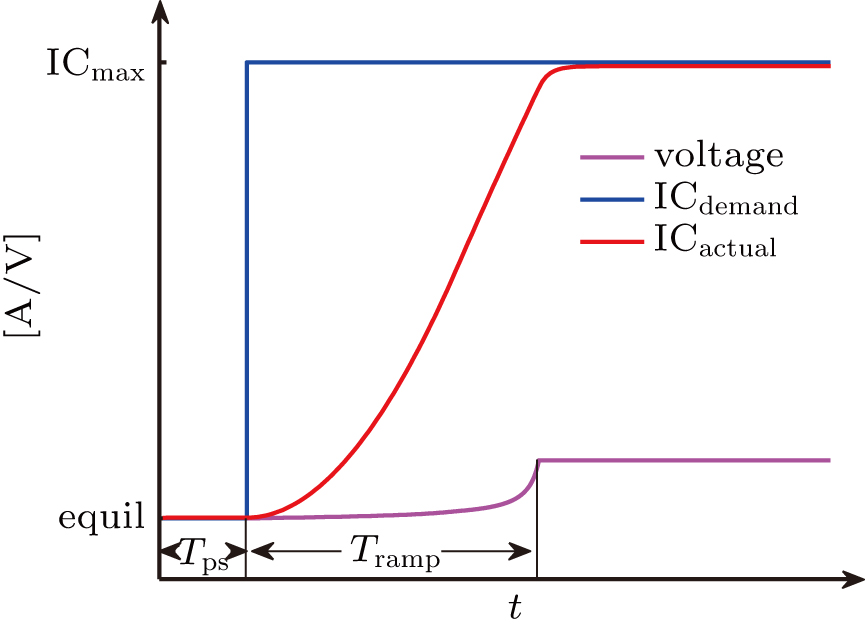
A comparison of the plasma response to active feedback control of VDE is made. According to the EAST active vertical instability control strategy, a pair of up–down symmetric anti-series connected internal coils (ICs) is located inside VV but outside PP in the numerical model. The two IC coils are located at R = 7.0 m and Z = ± 3.0 m. Each coil has six turns and a resistance of 600 μΩ. The response delay (T_ps) time and the current ramp time (T_ramp) are both set to be 1 ms. A feedback control loop is built by using the IC coils.

The TSC feedback control loop is depicted in Fig. 3. A standard PD controller is used to compute the required current:

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Vertical position feedback control loop in TSC.

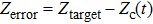
The required current ICk_demand plus the preprogrammed current I_pre (zero) is then sent to the power supply model, which is shown in Fig. 4. With the required current, the voltage is calculated from

The voltage Pt is then taken into the computation of the poloidal flux at the coils according to Faraday’s Law and Ohm’s Law.^[1] Given the magnetic field at the coils, the coil current density is computed according to Ampere’s Law:

On the other hand, the complete feedback control loop used in the TokSys is depicted in detail in Ref. [16] which is similar to the TSC’s. Its difference from the TSC control loop is mainly in two points. Firstly, the power supply system is depicted by a transfer function . Secondly the rigid RZIP model is used for describing the tokamak.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) Power supply model of the vertical control system in TSC.

In Ref. [9], it is indicated that in order to avoid the loss of control of vertical position (safe control), the maximum controllable displacement should be no less than 5% ⋅ a, and 10% ⋅ a should be achieved for robust control, where a is the tokamak minor radius. In simulation here, two control cases with initial displacements of 8 cm (safe control) and 16 cm (robust control) are designed. The active feedback control loop is used to recover Z_c. The focus is on the estimation of the least power supply requirements to achieve the two control targets. The maximum current limitation is abolished. The control current is improved gradually until Z_c can be successfully recovered. Computation results are listed in Table 7. The TSC gives a result that for safe control, the peak current is no less than 14 kA/turn, and for robust control, the peak current is about 28 kA/turn. The TokSys gives a very close evaluation that the peak current is 13.3 kA/turn for safe control and 26.5 kA/turn for robust control. A comparison shows that the two codes are in accord with each other in the sense of vertical instability control simulation.

Table 7.

Table 7.

Table 7. Comparison of peak control currents between the TSC and the TokSys. . Control level/cm Peak current/kA TSC TokSys 8 14.1 13.3 16 27.8 26.5

Table 7. Comparison of peak control currents between the TSC and the TokSys. .

In this paper, a comparison benchmark between the TSC and the TokSys for CFETR vertical instability control design is presented. Passive stability analyses of vacuum vessel and passive plates are made. The least power supply requirements for safe control and robust control of VDE are investigated. For all these analyses, the same tokamak plasma parameters are used for both codes. Although great model differences exist between the two codes, their agreement is found in a reasonable range. The TokSys uses a minimally complex linear rigid RZIP model which can quickly and accurately give an assessment of the electromagnetic interaction between the plasma and the surrounding conductors. The TSC solves full non-linear transport time-scale plasma evolution equations, and is good at comprehensively describing the tokamak plasma and its control systems. Mutual corroboration and complementation between the two codes will be beneficial to the CFETR vertical control design. The main purpose of simulation here is to build the code benchmark; the specific control design parameters are kept the same in both codes but optimization is not considered here, for the designs of other in-vessel components are not finished yet.