Cite this Article
Shao Gui-Fang, Zhu Meng, Shangguan Ya-Li, Li Wen-Ran, Zhang Can, Wang Wei-Wei, Li Ling. Structural optimization of Au–Pd bimetallic nanoparticles with improved particle swarm optimization method . Chinese Physics B, 2017, 26(6): 063601  
Permissions
Structural optimization of Au–Pd bimetallic nanoparticles with improved particle swarm optimization method
Shao Gui-Fang †, Zhu Meng, Shangguan Ya-Li, Li Wen-Ran, Zhang Can, Wang Wei-Wei, Li Ling
Department of Automation, Xiamen University, Xiamen 361005, China

 

† Corresponding author. E-mail: gfshao@xmu.edu.cn

Abstract

Due to the dependence of the chemical and physical properties of the bimetallic nanoparticles (NPs) on their structures, a fundamental understanding of their structural characteristics is crucial for their syntheses and wide applications. In this article, a systematical atomic-level investigation of Au–Pd bimetallic NPs is conducted by using the improved particle swarm optimization (IPSO) with quantum correction Sutton–Chen potentials (Q-SC) at different Au/Pd ratios and different sizes. In the IPSO, the simulated annealing is introduced into the classical particle swarm optimization (PSO) to improve the effectiveness and reliability. In addition, the influences of initial structure, particle size and composition on structural stability and structural features are also studied. The simulation results reveal that the initial structures have little effects on the stable structures, but influence the converging rate greatly, and the convergence rate of the mixing initial structure is clearly faster than those of the core-shell and phase structures. We find that the Au–Pd NPs prefer the structures with Au-rich in the outer layers while Pd-rich in the inner ones. Especially, when the Au/Pd ratio is 6:4, the structure of the nanoparticle (NP) presents a standardized PdcoreAushell structure.

PACS: 36.40.-c;52.65.Pp;61.46.Df
Keyword:bimetallic nanoparticles;stable structures;particle swarm optimization (PSO);simulated annealing
1. Introduction

Metallic NPs with the superior properties in the catalyst domain, have aroused a great deal of research interest.[1–7] Especially, bimetallic NPs, consisting of two different kinds of metal elements, exhibit very interesting properties that are not found from their corresponding pure metals due to the synergistic effects.[1,2] Among the noble metals Pt, Pd, Au, and Ag, Au and Pd nano-sized particles have been widely known as two of the best materials for catalyst.[3,4] Meanwhile, it was disclosed that the Au–Pd alloy NPs display higher catalytic activity and stability in various catalytic reactions.[5–8] However, the insufficient supply and considerable demand for Au result in the sharp increase in its price. Therefore, the development of bimetallic catalysts can make full use of the superiority of both metals.[9,10]

To date, a great number of studies have been conducted on experimental synthesis and theoretical analysis of Au–Pd alloy NPs. The Au–Pd metallic combinations have been prepared into different structures for various catalyst applications. The x-ray absorption fine structures and core-shell structures of Au–Pd bimetallic catalyst were built to achieve higher activity and selectivity of catalyst.[11,12] The polymer support polyaniline (PANI)-supported Au–Pd NPs with core-shell structure were prepared for selective oxidation of benzyl alcohol.[13] Pd-on-Au NPs were exploited to improve the nitroarene reduction reactions.[14] Besides the experimental methods, some researchers focus on investigating the structures and stabilities of alloy NPs owing to the fact that their chemical or physical properties are strongly dependent on their structures and atomic composition distributions. To further understand the catalytic mechanism of Au–Pd alloy NPs, it is necessary to determine the stable structures of Au–Pd alloy NPs theoretically. In our previous work, the single-crystalline and multiple-twinned structural stability of Au–Pd NPs were systematically investigated by an improved genetic algorithm.[2] Experimental results reveal that among all polyhedron, the truncated octahedron exhibits the best stability, while the worst one is the icosahedron. In addition, we also studied the potential effects on Au–Pd NPs based on the tight-binding potentials and the quantum corrected Sutton–Chen type many-body potentials.[9] It has been found that Au–Pd NPs with open surface structures (the tetrahexahedral (THH) NPs bounded with high-index {h, k, 0} (h > k > 0) facets) exhibited greatly enhanced catalytic activity owing to a much higher density of low coordination sites at the surface than at low-index facets.[9,15] Therefore, to further improve the chemical activity of Au–Pd alloy NPs, a feasible strategy is essential to study the high-index-faceted Au–Pd alloy NPs.

Due to the fact that the activity and selectivity of NP catalysts are usually determined by their structures, an in-depth investigation on the stable structures is crucial for understanding their catalytic performances. In recent years, many scientists have conducted a lot of researches on the structures of alloy NPs with different methods.[2,9,16–21] The genetic algorithm (GA) and the Monte Carlo algorithm are two of the most popular methods because of their generality and excellent searching ability.[17,19,20,22] Especially, the simulated annealing algorithm was successfully employed to explore the stable structure and segregation behavior of THH Pt–Pd–Cu–Au quaternary alloy NPs.[23] In addition, recently, the PSO has also been applied to the bimetallic NPs structural optimization.[18,24] Like the GA, the PSO also departs from random solutions and finds the optimal solution through iterations, but the PSO is simpler than the GA due to no GA’s “cross” (crossover) and “alternative” (mutation).[25,26] We have done some work on improving the PSO for the structural prediction of Pt–Pd alloy NPs.[18,24] However, there still exist some deficiencies, such as the low searching speed and easily converging into the local optimum when searching the optimal structures of large NPs. Therefore, a further improvement of PSO is needed to be better adapted to the structural optimum of Au–Pd alloy NPs.

In this paper, the relationships among the structures, energies, segregation behavior of Au–Pd NPs and the sizes ( 63 atoms, 443 atoms, 1417 atoms and 3285 atoms), Au/Pd ratios (changing from 1/9 to 9/1) are explored by employing the IPSO. The simulated annealing is adopted to enable the suboptimal solutions to mutate with a specified probability. In addition, to provide an insightful guidance for the practical preparation, synthesis and application of Au–Pd alloy NPs, the Warren–Cowley chemical short-range order (CSRO) parameter is used to clarify the rules of a structurally stable atomic arrangement of Au–Pd alloy NPs. The remainder of this article is arranged as follows. In Section 2, we briefly describe the simulation methods; in Section 3 we present the calculated results, discussion and comparisons with available results; the main conclusions are summarized in Section 4.

2. Simulation method

It is well known that the lower the potential energy is of Au–Pd alloyed NPs, the higher the stability of the NPs’ structures is.[2] Therefore, the key point of structural stability research is to find the lowest energy of the NPs. Theoretically, finding the stable structures of alloy NPs can be considered as a global optimization problem. In this article, Q-SC potentials are used to describe the inter-atomic interactions. In addition, an IPSO method is proposed for stable structural optimization of Au–Pd NPs.

2.1. Interatomic potential

As is well known, atomic scale simulation of the NPs is usually based on the interatomic potential. Hence, the accuracy of the description of the interatomic potentials plays a decisive role in investigating the structure of NPs. So far, the Q-SC potential has been verified to be suitable for exploring various basic properties of Au–Pd alloy NPs, such as the lattice parameter, cohesive energy, bulk modulus, elastic constants, phonon dispersion, vacancy formation energy, and surface energy.[2,27] According to the Q-SC potential,[27] the total energy of NPs can be expressed as

in which is defined as
with representing the distance between atom i and atom j, and being the repulsion between atom i and atom j; ρi denotes the local charge density of atoms and is in the following form:
c is a dimensionless parameter; a is the lattice constant obtained on condition that the temperature is zero degrees K. Moreover, n and m are integers that satisfy the relationship n > m. The potential parameters for Au and Pd are given in Table 1.

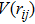
Table 1.

Potential parameters for Au and Pd.[2]

.
2.2. Improved particle swarm optimization (IPSO)

To adapt to the stable structure searching issue of Pt–Pd alloy NPs, we proposed an improved PSO method to solve this problem in our previous work,[18,24] in which the swap operator and swap sequence are put forward to reduce the probability of premature convergence into the local optimum. It includes three steps: 1) binary coding, by using 0 and 1 to indicate different atoms and 1 to N number the coordinates of all the atoms in the NPs; 2) updating with the swap operator and swap sequence; 3) exchange with variable precision.[24] The algorithm block diagram of the improved PSO can be found in Ref. [24].

First, randomly generate a group of particle sequences with a series of different combinations for initialization. The structure of each nanoparticle is represented by one particle. Then, the energy value of the particles can be calculated using the Q-SC potential equation. Besides, each particle moves according to its own flight speed in the solution space. In this process, the magnitude and direction of the velocity are controlled in each movement by both the current flight speed itself and the following two optimal positions: the optimal position for the current i particle and the optimal position for the entire particles. Each particle constantly moves as described above, eventually finds its optimal location. Particle i, will update its own pace and new location according to the following formula:

After the variation, the formula of the position calculation is

where represents the position of the particle i; represents the particle velocity of i; w is the inertia weight, while and are learning factors, usually equivalent to ; and are two random numbers between 0 and 1; represents the optimal position found so far by i; represents the optimal position of all the particles.

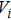
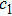
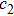
Finally, the exchange operation is conducted by randomly selecting a 0–1 pair in the sequence based on a given exchange probability.

However, only one exchange pair of 0 and 1 in each sequence will lower the searching speed. Meanwhile, all the suboptimal solutions are dismissed during each variation, which will cause the algorithm to easily converge into the local optima. Therefore, to make up these deficiencies in our previous PSO, some new attempts are made in this article.

First of all, the exchange pair K in each variable sequence is changed from the original fixed threshold into a variable value. The value of K is defined as

in which the atomnum represents the atom number of Au–Pd NPs, the generation is the maximum searching generation, i is the current searching generation. It is noted that in the initial process, exchange pair K is large, which means that the coding sequence has a high variety at the initial stage. Such an operation can accelerate the initial searching speed. But with i increasing K decreases and at the final stage, K is set to be 1, which means that the exchange pair is one, thereby avoiding over variation destroying the optimized results.

Secondly, the simulated annealing operator is added into the PSO to enable the suboptimal solutions to mutate with a specified probability instead of dismissing suboptimal solutions in our previous work. This will give the suboptimal solutions an opportunity to evolve into the optimal solutions. The concrete operation is given below.

If the potential energy of the ‘particle’ after variation is lower than the previous minimum energy, it will be replaced by the current potential energy of the ‘particle’. Otherwise, the ‘particle’ accepts the variation with a giving probability. The probability is obtained as follows:

where is the difference of energy between before and after the variation operation; denotes the temperature variation rate, which is always between 0 and 1; T represents the current temperature. The details of the pseudo code for the simulated annealing algorithm are shown in Algorithm 1.

Algorithm 1. Simulated annealing
3. Results and discussion
3.1. Effect of initial configuration

Due to the fact that the IPSO is used for searching the stable structure of NPs, the initial structures may affect its evolutional performance. Therefore, various initial configurations are employed, including a random mixture, core-shell and phase structures, to investigate their influences on stable structure.

As mentioned above, the THH NPs bound with high-index-facets have been proved to exhibit greatly enhanced stability compared with those with low-index facets.[9,15] Therefore, in this article the THH NPs bounded with 24 facets are chosen as the initial atomic configuration, and they can be produced according to the following steps:

generates a large cubic face-centered (fcc) single Au crystal;

using a square pyramid to cap each face, a five-polyhedral shape of single-crystalline Au NPs enclosed by 24{210} facets is produced;

Au and Pd atoms are randomly or orderly distributed in NPs by computer produced random seeds.

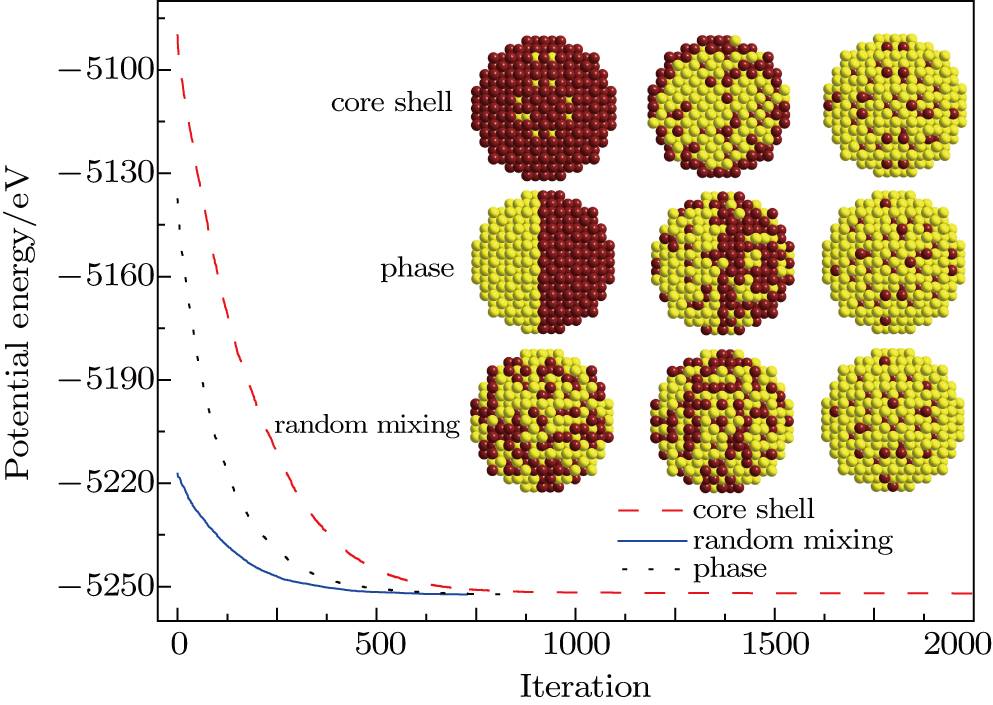
In addition, three different initial configurations, including the random mixing, core-shell and phase, are selected for comparative experiments as shown in Fig. 1.

Fig. 1. (color online) Initial cross-section atomic configurations of THH shape with (a) random mixing, (b) core-shell structure, and (c) phase structure for Au–Pd alloy NPs. Au atoms are in yellow and Pd atoms in brown.

At the same time, nine different atomic ratios with Au composition changing from 0.1 to 0.9 have also been selected to test the influence of initial structure on evolutional performance. Figure 2 reveals the convergence behaviors of those three initial structures at different amounts of Au content by using our proposed IPSO method. As shown in Fig. 2, for the same atomic ratio, they will converge to the same potential energies even though they start from different initial configurations. That means that the initial configuration has little effects on the stable structure. However, one can find that all curves (solid line) of adopting random mixing structures decline remarkably faster than those of the other two structures (dotted line) in each atomic ratio. That is to say, the mixing structure owns the fastest convergence speed. Therefore, we will adopt the mixing structure as the initial configuration for the following experiment.

Fig. 2. (color online) Comparison of convergence among three initial structures for THH NPs with 443 atoms and Au composition changing from 0.1 to 0.9.

Furthermore, to gain an insight into the performance of the corresponding structure evolving with those three different initial configurations, the NPs with 1417 atoms and 5:5 (Au: 708, Pd: 709) atomic ratio are chosen to be investigated in detail as shown in Fig. 3. It is obvious that the random mixing structure possesses lower initial potential energy and evolves faster. What is more, Fig. 3 shows the atomic structures during three different evolutional periods. It can be concluded that various initial structures will affect the intermediate evolution but have a minor effect on the final stable structure.

Fig. 3. (color online) Comparison of convergence for three different initial structures for THH Au–Pd alloy NPs with 1417 atoms and 5:5 atomic ratio.
3.2. Performance of IPSO

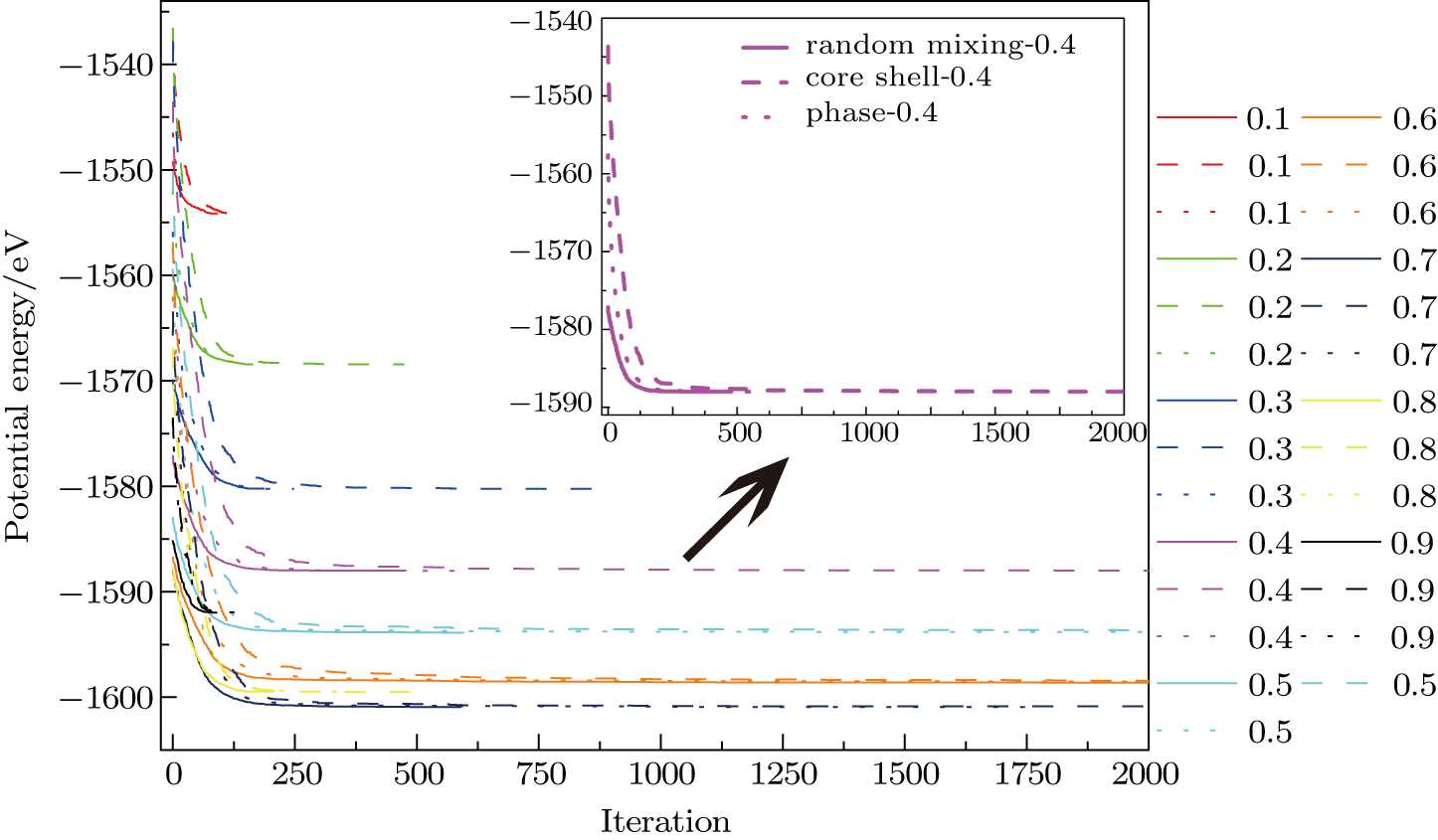
In order to verify the reliability and feasibility of IPSO, a comparison of IPSO with the classical PSO is conducted. Figure 4 shows the evolutional processes of classical PSO and IPSO on THH Au–Pd NPs with 1417 atoms. Clearly, IPSO possesses a faster convergence rate and converges to a lower energy than classical PSO, i.e., the lowest energy obtained by classical PSO and IPSO are –5223.499 eV and –5252.247 eV, respectively. The stable structures shown in Fig. 4 also prove that IPSO can search for a more symmetrical structure even though it starts from the similar initial structures.

Fig. 4. (color online) Comparison of evolutionary process of the potential energy between using the classical PSO and IPSO for THH Au–Pd alloy NPs with 1417 atoms and 5:5 atomic ratio.

To further explore the stability and reliability of the proposed algorithm, Au–Pd NPs with 443 atoms at Au/Pd equal to 5:5 (Au: 221, Pd: 222) is selected for repeating the experiments. Figure 5 reveals the results of experiments repeated 10 times for the classical PSO and IPSO. Obviously, the IPSO exhibits quite better stability with evolving to similar energy values, yet the classical PSO reaches different energy values at each trial. Meanwhile, the detailed final potential energies displayed in Fig. 5 prove our conclusion too.

Fig. 5. (color online) Comparison of result between repeated experiments of the classical PSO, and IPSO for THH Au–Pd alloy NPs with 443 atoms and 5:5 atomic ratio.
3.3. Stable structures

The optimized structures of Au–Pd NPs at different sizes and amounts of Au content by using IPSO are shown in Fig. 6. It can be seen that Au atoms preferentially aggregate on the surface, yet Pd atoms tend to locate inside. When the Au content is smaller, Au atoms and Pd atoms are commonly segregated on the surface, and Pd atoms prefer to occupy the vertexes and edges. For Au content of 50%, Au–Pd NPs exhibit a core-shell structure. With the increasing of Au content, Au atoms and Pd atoms are mixing inside.

Fig. 6. (color online) Structures of Au–Pd NPs with the lowest energy in different sizes and Au content values of 0.25, 0.5, and 0.75. Au atoms are in yellow and Pd ones are in brown.

Furthermore, the atomic ratio and size are thoroughly investigated. The results are depicted in Fig. 7. As shown in Fig. 7(a), the average potential energy per atom decreases with Au/Pd ratio increasing, which means that the average potential energy per atom strongly depends on the Au content. Moreover, it is verified by the experiments on NPs size as shown in Fig. 7(b), higher Au content possesses lower potential energy.

Fig. 7. (color online) Variations of average potential energy per atom of Au–Pd NPs with (a) Au/Pd ratio and (b) particle size, respectively.
3.4. Atomic distributions

To illustrate atomic distribution in greater detail, the atomic distribution function is used to analyze the stable structures. Here, the optimal structures of Au–Pd NPs are divided into several layers according to the distance between the atom and the center. Then we calculate Au and Pd fractions and numbers in each shell. Figure 8 shows the distributions of Au atoms and Pd atoms at different Au/Pd ratios (from 1:9 to 9:1). From the first row in Fig. 8, we can see that Au fractions are 0 at the first four layers, then its fractions are increasing, but still smaller than those of Pd atoms. When the Au–Pd ratios are 1:9 and 2:8, the outmost layer is almost equally shared by the Au and Pd atoms, yet there are more Au atoms occupying the outmost layers while the Au/Pd ratio is higher than 3:7. However, Au fractions increase greatly and are larger than those of Pd atoms among the four outer layers as shown in the second row of Fig. 8.

Fig. 8. (color online) Atom distributions of Au–Pd NPs with 1417 atoms. The 1st shell denotes the innermost shell (core) and the last shell denotes the outmost surface.

For instance, the three outer layers are fully filled with Au atoms with the fractions of Pd atoms being all zero. With the Au content rising on, more and more Au atoms tend to occupy the surface sites and the fractions of Pd atoms among the four outer layers are all 0 as shown in the third row of Fig. 8. It reveals that Au atoms possess stronger surface segregation behavior than Pd ones. Theoretically, the surface energy of Au atom is obviously lower than that of Pd, so Au can significantly reduce the surface energies of the whole nanoparticles on condition that the Au atoms are mostly distributed on the surface. Therefore, our experimental results are in agreement with theoretical predictions. We can expand this conclusion even further as follows: to retain the NPs in a lower energy state, the atoms with a higher surface energy tend to locate in the inner layer of NPs. On the other hand, the atoms with a lower surface energy always distribute to the outer layer of NPs.

In order to better understand this regularity of atomic distribution, the detailed distributions of fractional composition of Au and Pd atoms with different NPs sizes are conducted as shown in Fig. 9. Obviously, Au fractions at outer layers continuously rise with particle size increasing, yet Pd fractions decline rapidly. Especially, for NPs with 1417 and 3285 atoms, the fractions of Au atoms in the outside layer are 100% with the fractions of Pd atoms being 0, indicating that Au atoms have a strong preference to be located at the surface.

Fig. 9. (color online) Fractions of Au and Pd atoms in each shell with Au/Pd ratio fixed at 5:5.
3.5. Surface distribution

It is well known that the catalytic reactions almost take place on the surface of NPs. Therefore, the surface atom distribution plays a decisive role in determining the catalytic activity of NPs. Figure 10 illustrates the fractions of Au atoms in each shell under different Au/Pd ratios. It can be seen that with the increasing of Au content, Au atoms tend to first occupy the surface with higher fraction. For example, when the Au content reaches to 65% for NPs with 443 atoms, Au atoms completely fill the surface. At the same time, for NPs with 1417 atoms, Au atoms will fully occupy the surface when its content is bigger than 45%. Especially for the lower Au content, all the Au atoms will segregate to the surface with the Au fractions in inner layers being all zero. In addition, for a Au/Pd ratio equal to 1, 76.5% of surface atoms are Au atoms in NPs with 443 atoms, yet for NPs with 1417 atoms its content is 100%. All the experimental results reveal that Au atoms possess a stronger surface segregation behavior than Pd atoms.

Fig. 10. (color online) Fractions of Au atoms at each shell for different amounts of Au/Pd content.
3.6. Structural features of NPs

As analyzed above, the stable structures of Au–Pd NPs present a strong tendency for ordering. Therefore, it is necessary to investigate the characteristics of atomic bonding between Au atoms and Pd atoms. In this article, the CSRO parameter is calculated to analyze the bond characteristics of the Au–Pd NPs.[9] The CSRO is defined as follows:

In which, 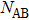is the nearest coordination number of B atoms around an A atom, N denotes the total coordination number in the nearest neighbor shell, and represents the atomic concentration of B. (In this paper, we designate Au as atom A). The value of CSRO ranges from −1 to 1. When the value of CSRO is 0, atoms A and B are distributed disorderly. A positive value of CSRO indicates the segregation distribution, while a negative value represents an ordered distribution.[9]

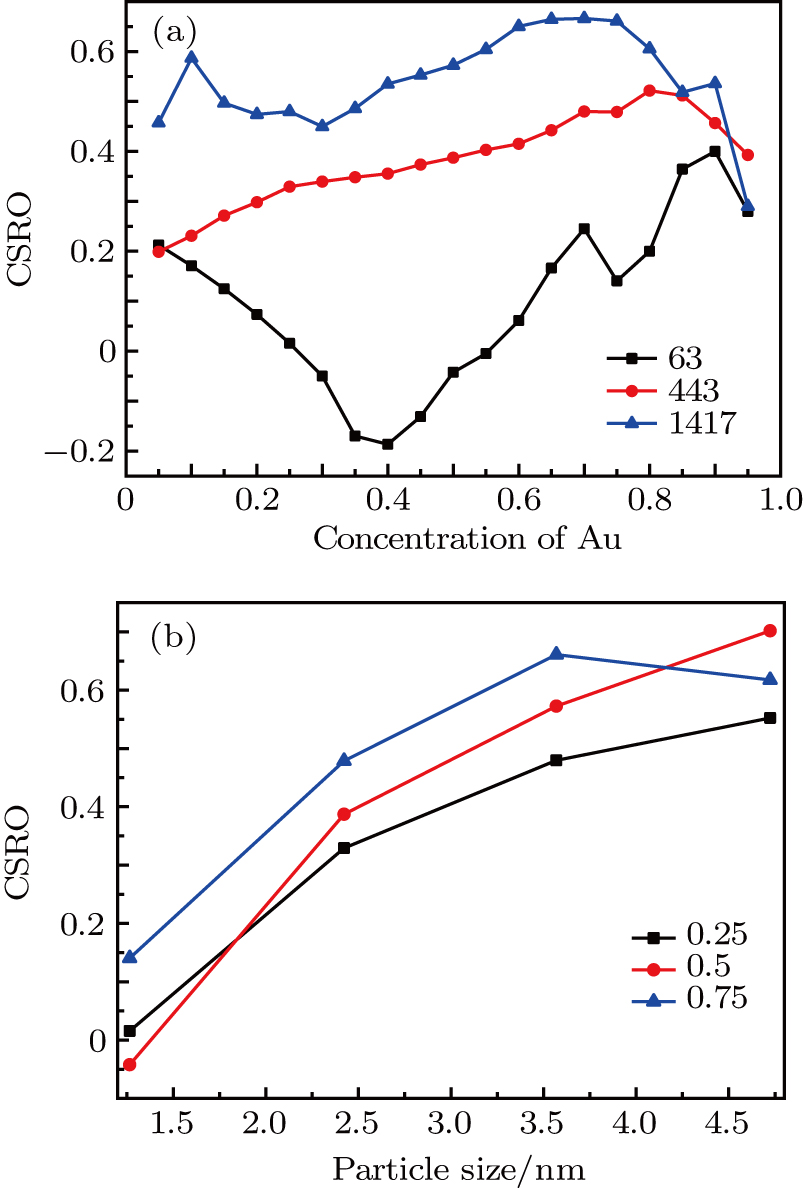Firstly, to explore the influence of Au concentration on the CSRO parameters, the CSRO values of Au–Pd NPs with Au concentrations ranging from 5% to 95% at three different NPs sizes are calculated. As shown in Fig. 11(a), the CSRO changes with the concentration of Au atoms increasing. For NPs with 443 and 1417 atoms, all CSRO values are positive, which suggests that their structures are all segregation distributions, but for NPs with 63 atoms, CSRO values are negative when the concentrations of Au range from 0.3 to 0.5, which indicates an ordered distribution. Moreover, it is evident that the curve of 443 atoms is under the 1417 ones, which means that the NPs with 1417 atoms possess a higher segregation degree. These results are in correspondence with the results of Fig. 9.

Fig. 11. (color online) Variations of the CRSO value for Au–Pd NPs with (a) Au atom concentration and (b) particle size.

Meanwhile, the influence of particle size on the CSRO parameters is also studied by computing the CSRO values of Au–Pd NPs with NPs size ranging from 1.25 nm to 4.75 nm at three different Au concentrations, which is depicted in Fig. 11(b). It can be seen that all CSRO values are positive except those of the NPs with Au concentration 0.5 in 1.25 nm size, which means that the NPs all present a segregation distribution. Moreover, the CSRO values rise with particle size increasing, indicating that the larger the particle size, the higher the segregation degree is.

4. Conclusions

In this article, an improved PSO (IPSO) algorithm is proposed to optimize the structures of THH Au–Pd alloy NPs. In order to improve the convergence speed of PSO, the simulated annealing mutation operator is introduced into the PSO algorithm. Through a comparison with the classical PSO algorithm, it is proved that the IPSO can find the structures with lower energies, i.e., the IPSO is verified to be more reliable and more effective. Meanwhile, the IPSO is adopted to investigate the structural stabilities and structural features of Au–Pd alloy NPs. The effects of different initial structures, particle sizes and Au/Pd ratios are considered. It is found that the initial structures have little effect on the stable structure, but evidently influence the convergence rate of the IPSO. Meanwhile, the mixing initial structure is proved to converge fastest in the three different initial structures. Moreover, the structural stability of Au–Pd NPs is really sensitive to the particle size and Au/Pd ratio, namely with the particle size and Au/Pd ratio increasing, the average potential energy obviously decreases. Beside, Au atoms tend to be located at the outer layers of the NPs, yet Pd atoms prefer the inner ones. Furthermore, by calculating the CSRO values of Au–Pd NPs with different particle sizes, we find that the larger the particle size, the higher the degree of segregation is, i.e., the larger Au–Pd NPs display a more obvious segregation distribution. In conclusion, our comprehensive understanding of the structural stability and structural characteristics of Au–Pd alloy NPs may contribute to their experimental syntheses and widespread applications. In addition, the IPSO is successfully employed in the structural optimization of Au–Pd NPs, and it may be extended to investigating other NPs.

Reference
[1] Ismail R Johnston R L 2010 Phys. Chem. Chem. Phys. 12 8607
[2] Shao G F Tu N N Liu T D Xu L Y Wen Y H 2015 Physica 70 11
[3] Huang R Wen Y H Shao G F Zhu Z Z Sun S G 2014 RSC Adv. 4 7528
[4] Adams B D Chen A 2011 Mater. Tody 14 282
[5] Noh S Jun H S 2016 RSC Adv. 6 84334
[6] Wei X Yang X F Wang A Q Li L Liu X Y Zhang T Mou C Y Li J 2012 J. Phys. Chem. 116 6222
[7] Wong M S Alvarez P J J Fang Y L Akcin N Nutt M O Miller J T Heck K N 2009 J. Chem. Technol. Biotechnol. 84 158
[8] Shao M W Wang H Zhang M L Ma D D D Lee S T 2015 Appl. Phys. Lett. 64 243110
[9] Shao G F Zheng W X Tu N N Liu T D Wen Y H 2015 Acta Phys. Sin. 64 013602 in Chinese
[10] Wang D S Li Y D 2011 Adv. Mater. 23 1044
[11] Balerna A Evangelisti C Schiavi E Vitulli G Bertinetti L Martra G Mobilio S 2013 15th InternationalConference on X-ray Absorption Fine Structure Beijing July, 22–28, 2012 430 012052
[12] Ding Y Fan F R Tian Z Q Wang Z L J 2010 J. Am. Chen. Soc. 132 12480
[13] Marx S Baiker A 2009 J. Phys. Chem. 113 6191
[14] Pretzer L A Heck K N Kim S S Fang Y L Zhao Z Guo N Wu T P Miller J T Wong M S 2016 Catalysis Today 264 31
[15] Lu C L Prasad K S Wu H L Ho J A Huang M H 2010 J. Am. Chem. Soc. 132 14546
[16] Bruma A Ismail R Paz-Borbon L O Arslan H Barcar G Fortunelli A Li Z Y Johnston J L 2013 Nanoscale 5 646
[17] Liu T D Zheng J W Shao G F Fan T E Wen Y H 2015 Chin. Phys. 24 033601
[18] Shao G F Wang T N Liu T D Chen J R Zheng J W Wen Y H 2015 Comput. Phys. Commun. 186 11
[19] Oh J S Nam H S Choi J H Lee S C 2013 International Conference on Mathematical Modelling in Physical Sciences Budapest September, 3–7, 2012 410 012084
[20] Johnston R L 2003 RSC Adv. 22 4193
[21] Chen Z H Jiang X W Li J B Li S S 2013 J. Chem. Phys. 138 214303
[22] Deng L Deng H Q Xiao S F Tang J F Hu W Y 2013 RSC Adv. 162 293
[23] Lu X Z Shao G F Xu L Y Liu T D Wen Y H 2016 Chin. Phys. 25 053601
[24] Liu T D Chen J R Hong W P Shao G F Wang T N Zheng J W Wen Y H 2013 Acta Phys. Sin. 62 193601 in Chinese
[25] Tang J 2010 Computer Technology and Development 20 213 in Chinese
[26] Tanweer M R Sure S Sundararajan N 2015 Information Sciences 294 182
[27] Wang Z G Huang R Wen Y H 2012 Acta Phys. Sin. 61 166102 in Chinese