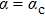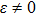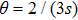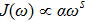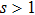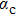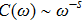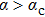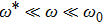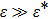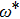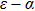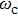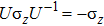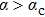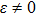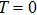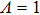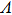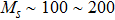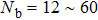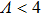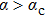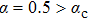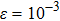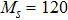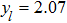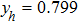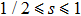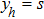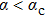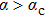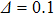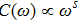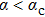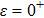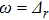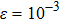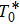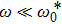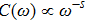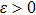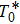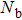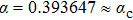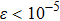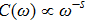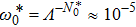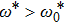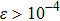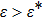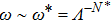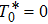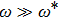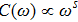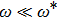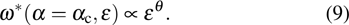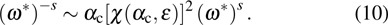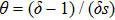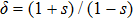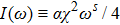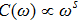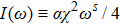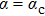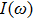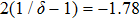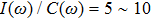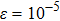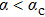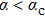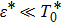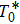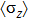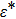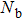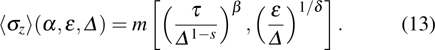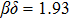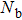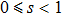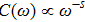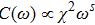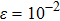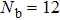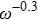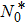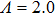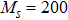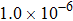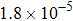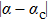3.1.
 -behavior in the small frequency regime
-behavior in the small frequency regimeFor the Ohmic (s = 1) and the super-Ohmic (
 ) baths, the small frequency behavior of C(ω) in the delocalized phase obeys the Shiba relation,[35] which in our notation reads[12]
) baths, the small frequency behavior of C(ω) in the delocalized phase obeys the Shiba relation,[35] which in our notation reads[12]
Here

is the local spin susceptibility. The proof in Ref. [
35] applies also to the case with a finite bias, but not to the localized phase at

for the Ohmic bath. This exact relation was used to test the quality of various approximate results for SBM.
[11,12,19,36–39]There have been attempts to generalize the Shiba relation to (i) sub-Ohmic bath, (ii) with finite bias, and (iii) strong coupling regime
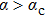 . Such a generalized relation, if it exists, would imply a universal long time behavior
. Such a generalized relation, if it exists, would imply a universal long time behavior
 for any s values, coupling strength α (except at the critical point
for any s values, coupling strength α (except at the critical point
 and ε = 0), and spin parameters
and ε = 0), and spin parameters
 and ε. Up to now these activities received partial success only. Florens and others[40] proved Eq. (8) for the sub-Ohmic bath, based on an exact relation from the perturbation theory in Majorana representation. However, their proof applies only to delocalized phase at the symmetry point ε = 0. The numerical results from the approximate perturbation theory built on a unitary transformation fulfils Eq. (8) exactly for the sub-Ohmic bath with[41,42] or without[18] bias in the weak to intermediate coupling. In the strong coupling regime
and ε. Up to now these activities received partial success only. Florens and others[40] proved Eq. (8) for the sub-Ohmic bath, based on an exact relation from the perturbation theory in Majorana representation. However, their proof applies only to delocalized phase at the symmetry point ε = 0. The numerical results from the approximate perturbation theory built on a unitary transformation fulfils Eq. (8) exactly for the sub-Ohmic bath with[41,42] or without[18] bias in the weak to intermediate coupling. In the strong coupling regime
 the fulfilment is good but not exact. This leaves the question open whether the Shiba relation holds in the biased strong coupling regime of the sub-Ohmic SBM.
the fulfilment is good but not exact. This leaves the question open whether the Shiba relation holds in the biased strong coupling regime of the sub-Ohmic SBM.
As stated above, the inherent truncation errors of NRG hinder it from the quantitative confirmation/falsification of the generalized Shiba relation. However, qualitatively, it is possible to check the factors on the right-hand side of Eq. (8) each for a time. In this section, we will show that
 holds for the sub-Ohmic SBM with general α and ε. In Fig. 6, data are presented to further support that
holds for the sub-Ohmic SBM with general α and ε. In Fig. 6, data are presented to further support that
 for general α and ε values.
for general α and ε values.
In Fig. 1, we first present the
 -dependence of C(ω) obtained from NRG under bias, in order to gauge the choice of
-dependence of C(ω) obtained from NRG under bias, in order to gauge the choice of
 in our study. The energy flows (Fig. 1(a)) and C(ω) (Fig. 1(b)) are shown for a sub-Ohmic bath s = 0.8 in the strong coupling regime
in our study. The energy flows (Fig. 1(a)) and C(ω) (Fig. 1(b)) are shown for a sub-Ohmic bath s = 0.8 in the strong coupling regime
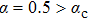 , with a finite bias
, with a finite bias
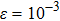 . We use a series of
. We use a series of
 values from
values from
 to
to
 with
with
 and
and
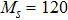 . In Fig. 1(a), for a given
. In Fig. 1(a), for a given
 , the excitation energies
, the excitation energies
 (i = 1, 2, 3) first flow to an unstable fixed point (with
(i = 1, 2, 3) first flow to an unstable fixed point (with
 ) in the small N regime. After a crossover
) in the small N regime. After a crossover
 , they flow to the stable fixed point (with
, they flow to the stable fixed point (with
 ) in the large N limit. We found that the unstable fixed point in the small N regime is the same as the weak-coupling fixed point of the SBM in the non-bias case (dashed lines obtained using α = 0 and ε = 0). With
) in the large N limit. We found that the unstable fixed point in the small N regime is the same as the weak-coupling fixed point of the SBM in the non-bias case (dashed lines obtained using α = 0 and ε = 0). With
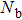 increasing geometrically, the crossover
increasing geometrically, the crossover
 increases linearly, showing that the associated energy scale
increases linearly, showing that the associated energy scale
 decreases to zero as a negative power of
decreases to zero as a negative power of
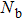 . This supports that the unstable fixed point (dashed lines in Fig. 1(a)) will extend to infinitely large N in the limit
. This supports that the unstable fixed point (dashed lines in Fig. 1(a)) will extend to infinitely large N in the limit
 and it is the true fixed point of the biased SBM. In this biased fixed point, ε flows to infinity and the spin is effectively decoupled from the bath, leading to the same excitation levels as the free boson chain.
and it is the true fixed point of the biased SBM. In this biased fixed point, ε flows to infinity and the spin is effectively decoupled from the bath, leading to the same excitation levels as the free boson chain.
Figure 1(b) shows the corresponding C(ω), which has two different power-law regimes:
 in the low frequency regime
in the low frequency regime
 , and
, and
 in the high frequency regime
in the high frequency regime
 . NRG data for s = 0.8 gives
. NRG data for s = 0.8 gives
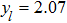 and
and
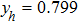 . With increasing
. With increasing
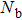 , the crossover frequency
, the crossover frequency
 decreases to zero as a negative power of
decreases to zero as a negative power of
 , proving that
, proving that
 is the correct result of the biased SBM (dashed line in Fig. 1(b)). Our results for other s values in
is the correct result of the biased SBM (dashed line in Fig. 1(b)). Our results for other s values in
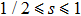 agree with
agree with
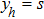 within an error of 2% (not shown).
within an error of 2% (not shown).
For
 , the NRG results converge with much more difficulty with increasing
, the NRG results converge with much more difficulty with increasing
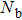 . In Fig. 2, we show the strong coupling data (
. In Fig. 2, we show the strong coupling data (
 ) for s = 0.3. Both the energy flow and C(ω) have
) for s = 0.3. Both the energy flow and C(ω) have
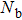 -dependent crossover scales. With
-dependent crossover scales. With
 increasing to 60, a clear trend can be seen that the
increasing to 60, a clear trend can be seen that the
 -converged levels flow towards the free boson energy levels (Fig. 2(a)). For both
-converged levels flow towards the free boson energy levels (Fig. 2(a)). For both
 and
and
 , the section of C(ω) with ωs behavior extends to smaller ω with increasing
, the section of C(ω) with ωs behavior extends to smaller ω with increasing
 (Fig. 2(b)). The shift of C(ω) with
(Fig. 2(b)). The shift of C(ω) with
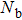 has an apparent scaling form and an analysis for
has an apparent scaling form and an analysis for
 could be carried out to extract the correct exponent, as done in Ref. [31]. Here in Fig. 2(b), we only mark out the expected asymptotic ωs line for guiding the eye. With this understanding of the
could be carried out to extract the correct exponent, as done in Ref. [31]. Here in Fig. 2(b), we only mark out the expected asymptotic ωs line for guiding the eye. With this understanding of the
 -dependence of C(ω), in the rest of this paper, we only show the physically correct results
-dependence of C(ω), in the rest of this paper, we only show the physically correct results
 obtained using sufficiently large
obtained using sufficiently large
 .
.
In Fig. 3, we investigate the influence of ε on C(ω) for α values ranging from weak coupling
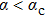 (Fig. 3(a)) to strong coupling
(Fig. 3(a)) to strong coupling
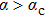 (Fig. 3(b)) for s = 0.8 and
(Fig. 3(b)) for s = 0.8 and
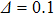 . It is seen that
. It is seen that
 in the small frequency limit for all parameters.In Fig. 3(a), for the small coupling α = 0.1 (dash-dotted lines), C(ω) does not change with ε up to
in the small frequency limit for all parameters.In Fig. 3(a), for the small coupling α = 0.1 (dash-dotted lines), C(ω) does not change with ε up to
 and the three curves for ε = 0, 10−3, and 10−5 overlap. While for a moderate coupling α = 0.4 (dashed lines), a slight downward shift is observed between
and the three curves for ε = 0, 10−3, and 10−5 overlap. While for a moderate coupling α = 0.4 (dashed lines), a slight downward shift is observed between
 and
and
 and the lines for ε = 0 and 10−5 overlap. C(ω) is most sensitive to ε when α is close to
and the lines for ε = 0 and 10−5 overlap. C(ω) is most sensitive to ε when α is close to
 . The same trend is observed in Fig. 3(b) for the strong coupling regime.
. The same trend is observed in Fig. 3(b) for the strong coupling regime.
The universal
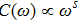 behavior observed so far in Figs. 1, 2, and 3 has a natural understanding. When the parity symmetry is already broken by a finite bias, the ground state of SBM can be tuned continuously on the α–ε plane, going from a delocalized state at
behavior observed so far in Figs. 1, 2, and 3 has a natural understanding. When the parity symmetry is already broken by a finite bias, the ground state of SBM can be tuned continuously on the α–ε plane, going from a delocalized state at
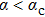 ,
,
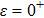 , through a half circle in a finite ε region, to the symmetry-spontaneously-broken state at
, through a half circle in a finite ε region, to the symmetry-spontaneously-broken state at
 ,
,
 , without passing the critical point. Therefore, the ground state has the same nature and no qualitative change is expected in the small ω limit of C(ω). Indeed, our NRG results for different s, α, and ε confirm that
, without passing the critical point. Therefore, the ground state has the same nature and no qualitative change is expected in the small ω limit of C(ω). Indeed, our NRG results for different s, α, and ε confirm that
 is a universal feature of SBM.
is a universal feature of SBM.
In the strong coupling case shown in Fig. 3(b), the same tendency is observed, i.e., with increasing ε, C(ω) shifts downwards and the most prominent change occurs near
 . The suppression of C(ω) can be understood as the weight transfer: with increasing ε,
. The suppression of C(ω) can be understood as the weight transfer: with increasing ε,
 increases and so does the weight of the zero-frequency δ peak. Due to the sum rule,
increases and so does the weight of the zero-frequency δ peak. Due to the sum rule,
 decreases uniformly. Comparing figs. 3(a) and 3(b), one sees that a broad peak forms for
decreases uniformly. Comparing figs. 3(a) and 3(b), one sees that a broad peak forms for
 and
and
 .
.
Besides the universal low frequency behavior of C(ω) that we focus on in this paper, the high frequency structure in C(ω) for the deep sub-Ohmic SBM (
 ) has also attracted a great deal of attention recently.[17,18,41] For small s values, a peak at the renormalized tunnelling
) has also attracted a great deal of attention recently.[17,18,41] For small s values, a peak at the renormalized tunnelling
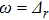 is observed in the strong coupling regime. It persists even in the localized phase
is observed in the strong coupling regime. It persists even in the localized phase
 . For α close to
. For α close to
 and small ε, another pronounced peak is observed at the crossover scale
and small ε, another pronounced peak is observed at the crossover scale
 . C(ω) thus has a two-peak structure for small s and close to the critical point. Here, our C(ω) for s = 0.3 and a weak bias
. C(ω) thus has a two-peak structure for small s and close to the critical point. Here, our C(ω) for s = 0.3 and a weak bias
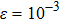 does have the two-peak structure, as shown by the dashed lines in Fig. 2(b). The high frequency peak is weak due to the over broadening of the log-Gaussian function. Decreasing the broadening parameter b from 1.2 to 0.8, the high frequency peak gets sharper and more pronounced, being consistent with previous results.[17,18,40]
does have the two-peak structure, as shown by the dashed lines in Fig. 2(b). The high frequency peak is weak due to the over broadening of the log-Gaussian function. Decreasing the broadening parameter b from 1.2 to 0.8, the high frequency peak gets sharper and more pronounced, being consistent with previous results.[17,18,40]
3.2. Equilibrium dynamics near QCPIn the above section, we established the universal ωs-behaviour of C(ω) in the full parameter space of SBM. In this section, we focus on the parameter regime near the QCP
 and study the critical properties of C(ω) under a bias. For the unbiased SBM,
and study the critical properties of C(ω) under a bias. For the unbiased SBM,
 is the only energy scale that controls the crossover between the stable fixed points (localized and delocalized fixed points) and the critical fixed point. Here ν is the critical exponent of the correlation length and z = 1 is the dynamical critical exponent.
is the only energy scale that controls the crossover between the stable fixed points (localized and delocalized fixed points) and the critical fixed point. Here ν is the critical exponent of the correlation length and z = 1 is the dynamical critical exponent.
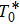 plays an important role in the temperature dependence of physical quantities close to QCP. At zero temperature, it also appears in the dynamical correlation function in the delocalized phase:
plays an important role in the temperature dependence of physical quantities close to QCP. At zero temperature, it also appears in the dynamical correlation function in the delocalized phase:
 for
for
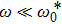 and
and
 for
for
 , and
, and
 .
.
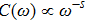 is the critical behavior which holds for arbitrarily small frequency at the exact critical point
is the critical behavior which holds for arbitrarily small frequency at the exact critical point
 , and is confined to
, and is confined to
 away from the critical point. As α approaches
away from the critical point. As α approaches
 ,
,
 tends to zero and the
tends to zero and the
 behavior will be recovered in the full frequency range.
behavior will be recovered in the full frequency range.
For the biased case,
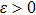 is another energy scale that influences the crossover between different behaviors of C(ω). Our NRG results for C(ω) at different α and ε can be understood in terms of the competition between ε and
is another energy scale that influences the crossover between different behaviors of C(ω). Our NRG results for C(ω) at different α and ε can be understood in terms of the competition between ε and
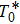 . Due to the difficulty of
. Due to the difficulty of
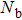 convergence for
convergence for
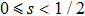 , here we show NRG data for s = 0.8, representing a typical case for
, here we show NRG data for s = 0.8, representing a typical case for
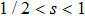 . Our conclusion also applies to
. Our conclusion also applies to
 , as will be discussed below.
, as will be discussed below.
In Fig. 4 and Fig. 5, we show the flow diagrams (Fig. 4) and C(ω) (Fig. 5) for
 (a),
(a),
 (b), and
(b), and
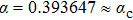 (c), respectively. For each α, ε varies from zero to 10−3. The purpose is to observe the influence of ε in the delocalized, localzied, and critical phases. Figures 4(a) and 5(a) are for
(c), respectively. For each α, ε varies from zero to 10−3. The purpose is to observe the influence of ε in the delocalized, localzied, and critical phases. Figures 4(a) and 5(a) are for
 . At ε = 0, the energy flow in Fig. 4(a) has a crossover at around
. At ε = 0, the energy flow in Fig. 4(a) has a crossover at around
 (solid circle), from the critical fixed point to the weak-coupling one. As ε increases from zero, the flow does not change for
(solid circle), from the critical fixed point to the weak-coupling one. As ε increases from zero, the flow does not change for
 and the crossover
and the crossover
 (empty squares) begins to decreases only for
(empty squares) begins to decreases only for
 . The corresponding evolution of C(ω) is shown in Fig. 5(a). For
. The corresponding evolution of C(ω) is shown in Fig. 5(a). For
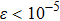 ,
,
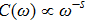 for
for
 and
and
 for
for
 . The crossover scale of the symmetric SBM is given by
. The crossover scale of the symmetric SBM is given by
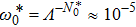 . With increasing ε, the crossover frequency
. With increasing ε, the crossover frequency
 increases and
increases and
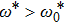 occurs only when
occurs only when
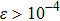 , corresponding to the occurrence of
, corresponding to the occurrence of
 in the flow diagram. A crossover scale
in the flow diagram. A crossover scale
 can be defined as such that for
can be defined as such that for
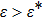 ,
,
 becomes significantly larger than
becomes significantly larger than
 , or equivalently,
, or equivalently,
 . For
. For
 , C(ω) stays same as the symmetric case (ε = 0) and
, C(ω) stays same as the symmetric case (ε = 0) and
 . For
. For
 , C(ω) is suppressed in the low frequency regime and
, C(ω) is suppressed in the low frequency regime and
 is set by ε.
is set by ε.
Figures 4(b) and 5(b) show the influence of ε in the localized phase. In Fig. 4(b), the excitation energy level at ε = 0 flows from the critical fixed point towards a two-fold degenerate fixed point, with the critical-to-localize crossover around
 (solid circle). Now we study the change of
(solid circle). Now we study the change of
 under bias (empty squares). With a vanishingly small ε, the degeneracy is lifted and the excited energy level has an upturn at an arbitrarily large
under bias (empty squares). With a vanishingly small ε, the degeneracy is lifted and the excited energy level has an upturn at an arbitrarily large
 , showing a crossover from the localized symmetric state to the biased state. We find that the crossover energy scale
, showing a crossover from the localized symmetric state to the biased state. We find that the crossover energy scale
 . With further increasing ε, the upturn moves to the left and for
. With further increasing ε, the upturn moves to the left and for
 ,
,
 occurs, which means that
occurs, which means that
 is now the crossover from the critical fixed point to the biased fixed point. NRG data give the critical-to-biased crossover
is now the crossover from the critical fixed point to the biased fixed point. NRG data give the critical-to-biased crossover
 . The critical exponent θ will be discussed with Fig. 5(c).
. The critical exponent θ will be discussed with Fig. 5(c).
In Fig. 5(b), the evolution of C(ω) with ε is shown, which looks similar to the case
 . That is, C(ω) does not change much with ε for
. That is, C(ω) does not change much with ε for
 and begins to be suppressed for
and begins to be suppressed for
 . It is noted that for a given
. It is noted that for a given
 , the degenerate-to-biased crossover at
, the degenerate-to-biased crossover at
 in the energy flow has no correspondence in C(ω): the latter has a perfect ωs behavior at
in the energy flow has no correspondence in C(ω): the latter has a perfect ωs behavior at
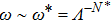 . The crossover in the energy flow will only show up in the temperature dependence of C(ω).
. The crossover in the energy flow will only show up in the temperature dependence of C(ω).
Figures 4(c) and 5(c) show the influence of ε on the flow and C(ω) in the critical regime
 . Since
. Since
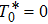 at this point, ε is the only energy scale that controls the critical-to-biased crossover in the energy flow and C(ω). Especially, Fig. 5(c) shows that
at this point, ε is the only energy scale that controls the critical-to-biased crossover in the energy flow and C(ω). Especially, Fig. 5(c) shows that
 for
for
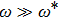 and
and
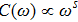 for
for
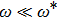 . We define a critical exponent θ as
. We define a critical exponent θ as
For
s = 0.8, the fitted exponent from Fig.
5(c) is

. Note that the same dependence of

on
ε applies to the

and
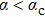
cases in the regime

, which are shown in panels (a) and (b) of figs.
4 and
5.
The NRG result in Fig. 5(c) shows that for
 ,
,
 with an ε-independent factor c. Combining this observation with the assumption that the Shiba relation Eq. (8) holds at
with an ε-independent factor c. Combining this observation with the assumption that the Shiba relation Eq. (8) holds at
 and
and
 (which will be discussed in Fig. 6 below), we can derive θ by equating the small and the large frequency expression at
(which will be discussed in Fig. 6 below), we can derive θ by equating the small and the large frequency expression at
 , giving
, giving
Employing the critical behavior

, one obtains

, giving
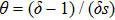
. From the exact expression
δ = 3 for

and
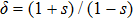
for

, we obtain
For
s = 0.8, this expression gives
θ = 1.111, which agrees well with the NRG result 1.12.
Having shown that
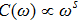 (
(
 ) for general α and ε values in the previous section, we now check the Shiba relation Eq. (8) at s = 0.8 using a fixed small frequency
) for general α and ε values in the previous section, we now check the Shiba relation Eq. (8) at s = 0.8 using a fixed small frequency
 . Figure 6 shows C(ω) and the right-hand side of Eq. (8)
. Figure 6 shows C(ω) and the right-hand side of Eq. (8)
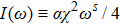 as functions of ε, for the same α values as in figs. 4 and 5. We find qualitative agreement between them for a wide range of ε. For
as functions of ε, for the same α values as in figs. 4 and 5. We find qualitative agreement between them for a wide range of ε. For
 (
(
 ), C(ω) shows the crossover from critical (power law dependence on ε) for
), C(ω) shows the crossover from critical (power law dependence on ε) for
 to the localized-like (delocalized-like) behavior (being constant) for
to the localized-like (delocalized-like) behavior (being constant) for
 , as expected. For
, as expected. For
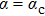 , a power-law dependence is observed, with the fitted exponent −1.88 (for C(ω)) and −1.84 (for
, a power-law dependence is observed, with the fitted exponent −1.88 (for C(ω)) and −1.84 (for
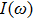 ), respectively, in reasonable agreement with the exact
), respectively, in reasonable agreement with the exact
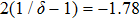 . It is notable that although C(ω) and
. It is notable that although C(ω) and
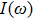 have more than 5 decades of variations in the range
have more than 5 decades of variations in the range
 , their ratio
, their ratio
 does not change much. This result supports the relation
does not change much. This result supports the relation
 .
.
The ratio also depends weakly on ω due to the slight inaccuracy in the exponent of NRG-produced C(ω). The uniform deviation from Eq. (8) observed here is more likely due to the error of NRG data than due to the invalidity of the Shiba relation. After all, a factor of 3 is a reasonable level of error in the NRG calculation of dynamical quantities,[11,12] considering the logarithmic error, truncation errors, as well as the approximation used to calculate C(ω) and χ.[33] It is expected that the agreement can be improved if we increase Ms and Nb, and extrapolate
 to unity, which will not be pursued here. The good agreement of the NRG value of the exponent θ and Eq. (11) is also consistent with
to unity, which will not be pursued here. The good agreement of the NRG value of the exponent θ and Eq. (11) is also consistent with
 , since equation (11) is derived from this assumption. For s = 0.3, it is more difficult to check the Shiba relation quantitatively due to much stronger boson state truncation error. As shown in Fig. 2(b), using
, since equation (11) is derived from this assumption. For s = 0.3, it is more difficult to check the Shiba relation quantitatively due to much stronger boson state truncation error. As shown in Fig. 2(b), using
 as large as 60, one can obtain the expected ωs behavior only in a narrow frequency window and for certain ε values. For those parameter regimes and frequencies where ωs behavior can be obtained, NRG results give a ratio
as large as 60, one can obtain the expected ωs behavior only in a narrow frequency window and for certain ε values. For those parameter regimes and frequencies where ωs behavior can be obtained, NRG results give a ratio
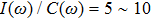 for the delocalized, critical, and the localized phases, much larger than the s = 0.8 case. This shows the difficulty of a quantitatively accurate NRG study for the deep sub-Ohmic SBM.
for the delocalized, critical, and the localized phases, much larger than the s = 0.8 case. This shows the difficulty of a quantitatively accurate NRG study for the deep sub-Ohmic SBM.
In Fig. 7(a), we fix
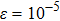 and plot C(ω) for different α values. For
and plot C(ω) for different α values. For
 , C(ω) increases with increasing α and the height of the peak reaches a maximum at certain
, C(ω) increases with increasing α and the height of the peak reaches a maximum at certain
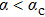 . With further increasing α, C(ω) begins to decrease uniformly, with the peak height suppressed. In Fig. 7(b), we show the maximum of C(ω) as functions of α for various εʼs. From this figure we can extract the α value at which the height of the peak in C(ω) reaches the maximum.
. With further increasing α, C(ω) begins to decrease uniformly, with the peak height suppressed. In Fig. 7(b), we show the maximum of C(ω) as functions of α for various εʼs. From this figure we can extract the α value at which the height of the peak in C(ω) reaches the maximum.
The phase diagram on the α–ε plane shown in Fig. 8 summarizes our results for C(ω) near the QCP. Close to
 and with very small ε, three regions I, II, and III of different nature are separated by a crossover line (squares with eye-guiding line). Regions I and III are continuously connected to the delocalized (
and with very small ε, three regions I, II, and III of different nature are separated by a crossover line (squares with eye-guiding line). Regions I and III are continuously connected to the delocalized (
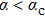 ) and localized phase (
) and localized phase (
 ) of the symmetric SBM, respectively. They are characterized by
) of the symmetric SBM, respectively. They are characterized by
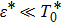 . In region I,
. In region I,
 with χ being the magnetic susceptibility. In region III,
with χ being the magnetic susceptibility. In region III,
 close to the saturate value. For each α, the crossover
close to the saturate value. For each α, the crossover
 in Fig. 8 is defined as the ε value at which the maximum of C(ω) decreases to 90% of its value at ε = 0.
in Fig. 8 is defined as the ε value at which the maximum of C(ω) decreases to 90% of its value at ε = 0.
In region II,
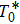 vanishes near
vanishes near
 and
and
 becomes the only characteristic energy scale. In this regime, the magnetization
becomes the only characteristic energy scale. In this regime, the magnetization
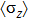 shows the quantum critical behavior as
shows the quantum critical behavior as
 , with δ being a critical exponent. The empty circles with eye-guiding line marks out the parameter at which C(ω) has a highest peak. Both the crossover line
, with δ being a critical exponent. The empty circles with eye-guiding line marks out the parameter at which C(ω) has a highest peak. Both the crossover line
 and the peak position can be extracted from the data in Fig. 7(b). It is observed that the location of the maximum peak resembles that of the maximum of entanglement entropy.[21] This is not a pure coincident since the crossover peak of C(ω) reflects a strong fluctuation near the critical point and it is therefore naturally related to the entanglement maximum.
and the peak position can be extracted from the data in Fig. 7(b). It is observed that the location of the maximum peak resembles that of the maximum of entanglement entropy.[21] This is not a pure coincident since the crossover peak of C(ω) reflects a strong fluctuation near the critical point and it is therefore naturally related to the entanglement maximum.
In the inset of Fig. 8, we fit the crossover line close to the QCP in a power law
with the obtained critical exponent
η = 1.99 for
s = 0.8. Note that the asymmetry of
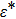
in

and

regimes means different pre-factors
c. Besides using
C(
ω) here, the critical behavior of

can also be determined by the scaling form of

obtained from the

scaling analysis of the NRG data.
[32] These two approaches give consistent results. For the second approach, the
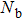
scaling analysis of NRG data gives (see Eqs. (31), (33), (35), (36) in Ref. [
32])
Here

and

is a two-variable scaling function. By comparing the magnitude of the two variables in Eq. (
13), one obtains

, giving

. Here,
β is the critical exponent of the order parameter. It is known that for
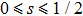
,
β = 1/2 and
δ = 3. For
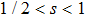
,
β is a function of
s whose explicit expression is unknown yet, and

.
[13,14,31,43,44] The NRG result
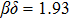
is in reasonable agreement with the fitted exponent
η = 1.99 in the inset of Fig.
8, showing the consistency of the static and dynamical approaches.
For
 , NRG calculation is hindered by the slow convergence with
, NRG calculation is hindered by the slow convergence with
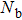 and it is difficult to obtain the quantitative data. However, we note that the scaling from Eq. (13) is obtained from the NRG calculation combined with the
and it is difficult to obtain the quantitative data. However, we note that the scaling from Eq. (13) is obtained from the NRG calculation combined with the
 scaling analysis for the full sub-Ohmic regime
scaling analysis for the full sub-Ohmic regime
 . It is stronger than the scaling ansatz of free energy which applies only to the regime
. It is stronger than the scaling ansatz of free energy which applies only to the regime
 .[43,44] The two exponents introduced above, θ and η, are not independent. We have
.[43,44] The two exponents introduced above, θ and η, are not independent. We have
 . This gives
. This gives
 , meaning
, meaning
 . This is a relation independent of the validity of hyperscaling relation.
. This is a relation independent of the validity of hyperscaling relation.