† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 51262032).
This study prepares a group of single crystalline β-Zn4Sb3 with Ge and Sn codoped by the Sn-flux method according to the nominal stoichiometric ratios of Zn4.4Sb3GexSn3 (x = 0–0.15). The prepared samples possess a metallic luster surface with perfect appearance and large crystal sizes. The microscopic cracks or defects are invisible in the samples from the back-scattered electron image. Except for the heavily Ge-doped sample of x = 0.15, all the samples are single phase with space group 
Thermoelectric material has become a promising functional material with its unique performance to achieve transformation between heat and electricity including thermoelectric generation and refrigeration. High cost and low thermoelectric conversion efficiency has been limiting the extensive application of thermoelectric materials for a long time in the past.[1–3] The thermoelectric properties are characterized by the dimensionless thermoelectric figure of merit — ZT, ZT = α2σT/κ, where α, σ, and κ are respectively the Seebeck coefficient, electrical conductivity and thermal conductivity of materials, T is the absolute temperature. The goals to develop and research new thermoelectric materials lie in the efforts to increase the electrical conductivity, Seebeck coefficient, and reduce the thermal conductivity simultaneously of the materials.[4,5]
β-Zn4Sb3, a novel p-type thermoelectric material with a high ZT value (1.40 at 675 K) in the medium temperature area (473 K–673 K), has aroused extensive attention.[6–9] The high TE performance of β-Zn4Sb3 mainly originates from the intrinsically low thermal conductivity for the complex and disordered crystal structure (about 0.65 W·m−1·K−1 of lattice thermal conductivity at room temperature).[10] Besides that, the component elements are low-cost and environmentally friendly. In order to further improve the ZT, the current Seebeck coefficient and electrical conductivity are relatively lower and should be improved. Besides the production methods, doping is a feasible approach to improve the thermoelectric properties which regulates the electronic structures and adjusts the carrier concentration.[11,12] In the past years, elements in the vicinity of Zn and Sb such as In, Pb, Sn, Cd, Bi, Mg, etc. were generally selected to dope the β-Zn4Sb3,[13–20] but Ge-substitution in β-Zn4Sb3 has been rarely reported so far. Wang et al. recently demonstrated the realization of a high thermoelectric figure of merit in Ge-substituted β-Zn4Sb3, the experimental results and theoretical calculations revealed that Ge substitution had a marked improvement on the Seebeck coefficient and the power factor.[21] However, the reported poor stability and weak mechanical property of polycrystalline β-Zn4Sb3 due to many micro-cracks or phase decomposition limit the practical applications.[22,23] Recently our work showed that β-Zn4Sb3 single crystals with superior performance can be obtained by the Sn-flux method,[24] and the stability of single crystalline β-Zn4Sb3 was improved compared with that of polycrystals.[25] In order to explore the effects of Ge substitution on the structure and properties of β-Zn4Sb3 single crystals, in this paper, Ge was doped in the β-Zn4Sb3 prepared by using the Sn-flux method, and Sn was inevitably incorporated in the synthesis process, so the Ge/Sn codoped single crystalline β-Zn4Sb3 were obtained. The influence of Ge/Sn codoping on the thermal stability and electrical transport properties has been investigated.
Ge/Sn codoped single crystalline β-Zn4Sb3 samples were prepared by using the Sn-flux method combined with melting and slow cooling technology. The high-purity elements of Zn (grains, 99.999%), Sb (grains, 99.999%), Ge (ingots, 99.999%), and Sn (grains, 99.999%) were weighed according to the stoichiometric ratios of Zn:Sb:Ge:Sn = 4.4:3:x:3 (x = 0, 0.03, 0.05, 0.075, 0.1, 0.15) as raw materials, the slightly additional Zn in the raw materials was aimed to compensate for the Zn loss during the synthesis process because of the relatively higher saturated vapor pressure of Zn. The weighed mixtures were loaded into quartz ampoules and sealed after evacuation. The quartz ampoules were then placed in a box furnace and heated to 853 K for 2 h. The mixture was held at this temperature for 12 h, and then cooled to 753 K for 15 min, followed by cooling to 593 K for 40 h. The mixture was held at this temperature before the molten flux was separated from the mixture by centrifugation.
The crystalline structure and phase were characterized by x-ray diffractometer (XRD; Ultima IV). The chemical compositions and back-scattered electron image (BSI) of the samples were obtained by electron probe microanalysis (EPMA; JXA-8230); when analyzing the actual content of each element, the average value of ten test points across the sample was gained for the same sample. The Hall coefficient RH at room temperature of the single crystalline β-Zn4Sb3 samples were measured using the Hall measurement system (Nanometrics HL5500 Hall System) in 0.55-T magnetic fields. The melting point and thermal stability were measured by the thermogravimetricdifferential thermal analysis (TG-DSC; STA449F3 Jupiter) in open alumina crucibles with a heating rate of 10 K/min and high-purity nitrogen was used as purge gas. The electrical conductivity σ and the Seebeck coefficient α were measured from 300 K to 660 K in a vacuum. When measuring the Seebeck coefficient, Konstantan (Ni: 40%) was used as a reference sample with a temperature difference maintained below 2 K. The Seebeck coefficient α of the samples was calculated using the formula α = ΔE/ΔT, where ΔE is the electric potential. The electrical conductivity σ of the samples was measured using the direct current (DC) four probe method with 20-mA DC.
The crystal growth results show that the introduction of slight Ge can yield perfect single crystals. As an example, the morphology image and BSI of the x = 0.075 sample are shown in Fig.
 | Fig. 1. The morphology (a) and back-scattered electron image (BSI) (b) of the single crystal sample with the nominal composition of Zn4.4Sb3Ge0.075Sn3 prepared by Sn-flux method. |
The sample phase compositions were identified by powder XRD shown in Fig. 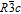
The actual compositions of all the samples are listed in Table
| Table 1. Actual compositions, carrier concentration n, Hall coefficient RH, and carrier mobility µH at room temperature for single crystalline β-Zn4Sb3 samples prepared using the Sn flux method based on the nominal stoichiometric ratios of Zn4.4Sb3GexSn3 (x = 0–0.15). . |
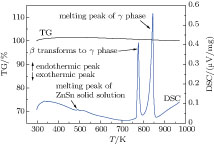
Figure
The Hall coefficient RH was measured at room temperature to determine the electrical properties, and the carrier concentration n, and carrier mobility µH were obtained from the measured RH and σ at 300 K using the equations, n = 1/(e|RH|) and µH = |RH|×σ, respectively, where e is the electron charge (Table
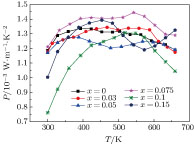
Figure
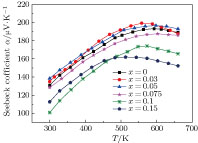
The temperature dependence of the Seebeck coefficient for all β-Zn4Sb3 samples is shown in Fig.
Figure
In this paper, Ge/Sn codoped single crystalline β-Zn4Sb3 with space group 
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] |