† Corresponding author. E-mail:
We theoretically study the differential conductance of a graphene/graphene superconductor junction, where the valley polarization of Dirac electrons is considered in the nonsuperconducting region. It is shown that the subgap conductance will increase monotonically with the valley-polarization strength when the chemical potential µ is near the Dirac point µ ≤ 3Δ (Δ is the superconducting gap), whereas it will decrease monotonically when µ is far away from the Dirac point, µ ≥ 5Δ. The former case is induced by the specular Andreev reflection while the retro-reflection accounts for the later result. Our findings may shed light on the control of conductance of a graphene superconductor junction by valley polarization.
Since graphene was exploited successfully by Geim and Novoselov a decade ago,[1] a surge of experimental and theoretical research on graphene has been made. The graphene subject will continue to attract much attention of researchers, because many topics of condensed matter physics can be done and extended in the graphene platform[2–6] due to the material advantages or, more specifically, the linear energy dispersion relation of Dirac electrons in just one-atom-layer thick and honeycomb-like materials.
Recently, valleytronics as a new discipline is increasingly rising and referred to as the electronics based on the valley degree of freedom of electrons in two-dimensional (2D) honeycomb lattice materials such as graphene, silicene, MoS2.[7–11] Valleytronics concerns the exploitation of the two degenerate but inequivalent Dirac points K, K′ of the Brillouin zone related by the time-reversal symmetry. Several very recent experimental works[12–14] have successfully measured the valley currents in the monolayer or bilayer graphene system, and this will further ignite new interest in exploring the valley degree of freedom of Dirac electrons to fabricate quantum devices.
The main challenge in valleytronics is to generate, manipulate, and detect the valley currents; so many works have been dedicated to those three aspects for possible applications in the future valley-based electronic devices.[15–18] In our previous works, we have studied using the valley polarization to control the Cooper-pair transport in graphene superconductor systems like realizing a \pi-state Josephson junction or splitting Cooper pair in real space.[19,20] Along the same route, in this work we will continue to study the valley polarization effect on the differential conductance of a graphene/superconductor graphene (G/GS) junction and aim to distinguish the specular Andreev reflection and retro Andreev reflection by using the very different transport properties. The specular Andreev reflection is famous in the graphene system that the reflected hole will not lie in the same band of the impinging electron upon the junction interface.[21] In graphene, this has been proved probable when the chemical potential is near the Dirac point.
Based on a low-energy continuum model and the Dirac Bogoliubov–de-Gennes equation, we found that the subgap conductance of the G/GS junction exhibits very different behaviors, it can either increase or decrease with the valley polarization of Dirac electrons, which depends on the dominant process of the specular or retro Andreev reflection (AR). Therefore, the valley-polarized electrons can be used to distinguish these two AR processes.[21,22]
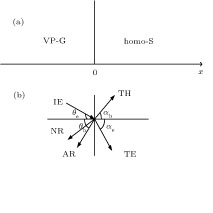
The system under consideration is a uniform graphene in the (x,y) plane, as shown in Fig.
In order not to mix with the valley polarization, the spin degree of freedom remains inactive and this simplification leads to a 16×16 matrix degenerating to two 4×4 matrices, which is the Nambu space ∗ pseudospin space of A and B sublattices. In the region x < 0, the two 4×4 matrices degenerate farther to four 2×2 matrices, where only the pseudospin spaces of A and B sublattices couple each other.
The low-energy electron dispersion arbitrarily close to the Dirac points K (k = 1) and K′ (k = −1) of a uniform graphene sheet is given by
 | (1) |
In order to form a Cooper pair, the incident electron (IE) and Andreev reflected hole must be taken from opposite corners K and K′ of the Brillouin zone on a G/GS junction interface, and thus Andreev reflection switches valleys in the graphene sheet.
For an incident electron from Dirac points K and K′, the wavevectors of the incoming electron and the reflected hole are
Further physics analysis shows: (i) when ε < µ − 2λ), the incident electron and the reflected hole are both in the same conduction band, and this is named intraband Andreev reflection or retro-AR; (ii) when µ > ε > µ − 2λ, there exists a forbidden band rather than a dot partitioning two kinds of ARs; (iii) when ε > µ, the reflected hole is an empty state in the valence band in another Dirac point, and this is interband AR or specular-AR.
The differential conductance of the tunnel junction at zero temperature which follows from the Blonder–Tinkham– Klapwijk formula is[23]
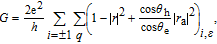 | (4) |
For the one-dimensional free and “ultra-relativity” electron, the number of propagating channels of an incident electron in the Dirac point K is
While that in K′ is
The total number of propagating channels of an incident electron is
Thus subgap conductance can be rewritten as
In accordance with Ref. [21] we define
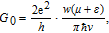 | (7) |
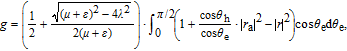 | (8) |
There are eight independent parameters in the formula of the valley-polarized conductance g after integrating with respect to the incident angle θ e, which are Δ, µ, ε, U 0, φ, k, λ, and E z . To reduce the number of adjustable parameters, we set E z = λ, and have a combined valley polarization strength 2λ for Dirac point K and 0 for Dirac point K′ (as done in the former description). In the following calculations, we also set φ = 0, Δ = 1, U 0 = 22Δ.[19,21] Here U 0 is a finite value. After these assumptions there are only three independent parameters for the valley-polarized conductance g: ε, µ, and λ.
Let us estimate the amplitude of G
0 from Eq. (
 | (9) |
We first simply summarize the conductance of G/GS junction in Fig.
 | Fig. 2. (color online) Differential conductance versus bias voltage for λ = E z = 0. No valley polarization is considered here. |
For ε < µ, we have θh > 0 (we assume earlier θ e > 0), then θ h and θ e are on the same side and the Andreev reflected hole is in the conduction band, namely retro-AR, while for ε > µ, due to θ h < 0, θh is on the other side and the hole is in the valence band, namely specular-AR. Thus the normalized subgap conductance
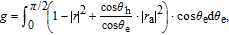 |
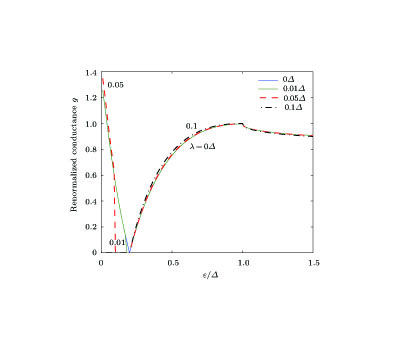
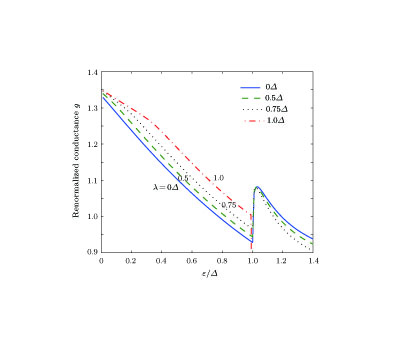
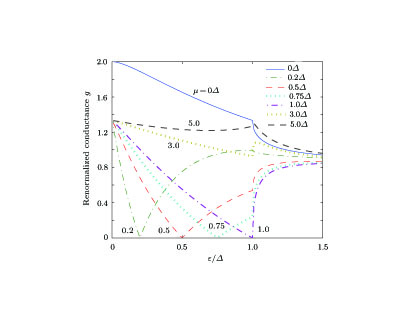
Secondly, we focus on the subgap conductance for µ = 0.2Δ in Fig.
As for case λ = 0Δ, the retro-AR dominates the process when ε < 0.2Δ, while the specular-AR dominates the reflection when ε > 0.2Δ. There is no valley polarization where the two kinds of Andreev reflection are separated by just a dot ε = µ = 0.2Δ. When µ = 0.2Δ and λ = 0.01Δ, the whole curve can be divided into 3 segments: i) For ε < 0.18Δ, we have the Andreev reflected angle θh > 0; ii) For 0.18Δ < ε < 0.2Δ, the wave number qh2 becomes an imaginary number and this kind of wave cannot spread across the valley polarization
The increase of λ leads to the decrease of the channel’s number factor N and the increase of the integrating factor via the decrease of the Andreev reflected angle θ
h, but the comprehensive effect of the increase of λ is the increase of the normalized subgap conductance g for the case µ = 0.2Δ. Regardless of whether the left-hand member and the right-hand member of any forbidden band in Fig.
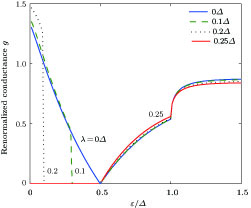
As for µ = 0.5Δ, there exist four curves for λ = 0Δ, 0.1Δ, 0.2Δ, and 0.25Δ in Fig.
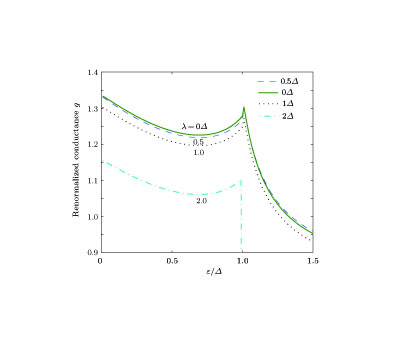
Fourthly, we analyze Fig.
In Fig.
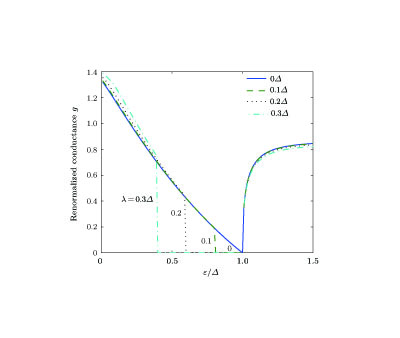
Finally, we want to emphasize the case of µ = 5Δ in Fig.
From the above discussion, we can make some concrete conclusions. At µ = 0, it is impossible that graphene is valleypolarized for this parabola-like dispersion relation, and there exists only specular-AR for all ε value. There are retro-AR and specular-AR for µ = 0.2Δ and µ = 0.5Δ), but only retro-AR survives at µ = 1.0Δ, µ = 3Δ, and µ = 5Δ. No specular-AR exists for µ > 1.0Δ. The theoretical calculations also show the subgap conductance increases with an increase of valley polarization strength for µ = 0.2Δ, 0.5Δ, 1.0Δ, and 3Δ, but decreases at µ = 5Δ. In particular, for the cases µ = 0.2Δ and µ = 0.5Δ, which simultaneously possess retro-AR and specular-AR, their subgap conductances have a common variation trend. Of course, the forbidden band conductance keeps zero invariably. The reason is as follows. The increase of valley polarization strength λ leads to the decrease of the AR angle θ h, which leads to the increase of the subap conductance; while the increase of λ responds to the decrease of the number of propagating channels N, which causes in turn the decrease of the subgap conductance. The practical variation of subap conductance depends on the competition of the two factors, θ h and N.
In summary, we have demonstrated theoretically that the differential conductance of the G/GS junction can be affected by the valley polarization, which is coming from the combined actions of the static staggered potential E z and the off-resonant circularly polarized light field strength λ. The subgap conductance of the G/GS junction decreases monotonously with an increase of valley polarization when the retro-AR is dominant. In contrast, the conductance will increase significantly with the valley polarization when the chemical potential µ ≤ 3Δ and the specular-AR mainly contributes to the conductance.
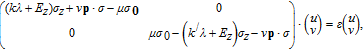 | (A1) |
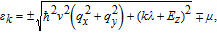 | (A2) |
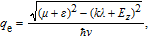 | (A3) |
 | (A4) |
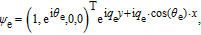 | (A5) |
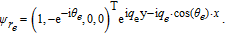 | (A6) |
For a right-moving hole with an incident angle qh, the eigenvector reads
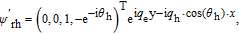 | (A7) |
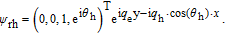 | (A8) |
In Fig.
Our findings demonstrated that the valley polarization can be used to distinguish the specular-AR from the retro-AR process in the G/GS junction.
For the region x < 0, electron and hole excitations are decoupled and described by the Dirac equation
For region x > 0, electron and hole excitations are coupled together by the superconducting pair potential Δ and described by the DBdG equation (Dirac–Bogoliubov–de Gennes)
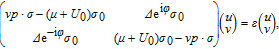 | (A9) |
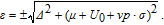 | (A10) |
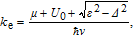 | (A11) |
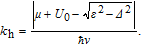 | (A12) |
For a right-moving electron-like quasi-particle (elq) at angle of transparent α e, the eigenvector reads
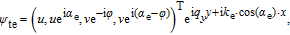 | (A13) |
 | (A14) |
For a right-moving hole-like quasi-particle (hlq) at the angle α h, the eigenvector reads
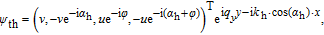 | (A15) |
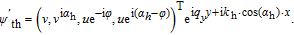 | (A16) |
In this letter, we just use the eigenvectors of a right-moving elq and a right-moving hlq in the circumstance Fig.
For an incident electron with angle θ
e in Fig.
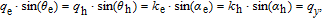 |
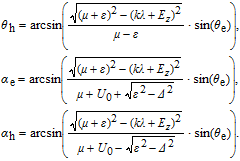 | (A17) |
Because Dirac equation and DBdG equation are all differential equation of the first order, we only apply the continuity condition at the interface x = 0
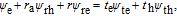 | (A18) |
Only the Andreev reflection angle θ h, Andreev reflection coefficient r a, and normal reflection coefficient r were quoted in the main text of this paper.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] |