† Corresponding author. E-mail:
The propagation of an intense laser pulse in an under-dense plasma induces a plasma wake that is suitable for the acceleration of electrons to relativistic energies. For an ultra-intense laser pulse which has a longitudinal size shorter than the plasma wavelength, λ p, instead of a periodic plasma wave, a cavity free from cold plasma electrons, called a bubble, is formed behind the laser pulse. An intense charge separation electric field inside the moving bubble can capture the electrons at the base of the bubble and accelerate them with a narrow energy spread. In the nonlinear bubble regime, due to localized depletion at the front of the pulse during its propagation through the plasma, the phase shift between carrier waves and pulse envelope plays an important role in plasma response. The carrier–envelope phase (CEP) breaks down the symmetric transverse ponderomotive force of the laser pulse that makes the bubble structure unstable. Our studies using a series of two-dimensional (2D) particle-in-cell (PIC) simulations show that the frequency-chirped laser pulses are more effective in controlling the pulse depletion rate and consequently the effect of the CEP in the bubble regime. The results indicate that the utilization of a positively chirped laser pulse leads to an increase in rate of erosion of the leading edge of the pulse that rapidly results in the formation of a steep intensity gradient at the front of the pulse. A more unstable bubble structure, the self-injections in different positions, and high dark current are the results of using a positively chirped laser pulse. For a negatively chirped laser pulse, the pulse depletion process is compensated during the propagation of the pulse in plasma in such a way that results in a more stable bubble shape and therefore, a localized electron bunch is produced during the acceleration process. As a result, by the proper choice of chirping, one can tune the number of self-injected electrons, the size of accelerated bunch and its energy spectrum to the values required for practical applications.
Since the generation of high power femtosecond laser pulses, numerous investigations have been devoted to the study of the interaction of high-intensity lasers with plasma. One application of the laser–plasma interaction is the generation of the high brightness and the high-energy electron beams in which electrons with energy up to 4.2 GeV, 6-pC charge, and 0.3-mrad divergence have been produced from a 9-cm-long capillary discharge waveguide.[1–12] The propagation of an intense laser pulse in an under-dense plasma induces a plasma wake that is suitable for the acceleration of the electrons to relativistic energies.[13–16] The electrons with sufficient initial kinetic energy can ride the plasma wake, staying in phase with the longitudinal electric field inside the wake and gaining energy. Because of the small structure of the wake field, i.e., its micron-scale longitudinal and transverse size, the bunches of a duration less than one plasma period have to be injected into the laser wake field in order to get high-quality electron bunches. However, the effective acceleration mechanism occurs when the ambient plasma electrons contribute to the injection process (self-injection). The self-injection process is explained by the two physical mechanisms: wave-breaking (the longitudinal self-injection),[17,18] and the bubble regime (transverse self-injection).[19–21] The bubble regime is a multidimensional effect, where the symmetric transverse ponderomotive force of the laser expels the electrons radially from the propagation axis and creates a spherical region (bubble) devoid of the plasma electrons behind the laser. This bubble moves with a velocity equal to the group velocity of the laser pulse in the plasma. An intense charge separation electric field inside the moving bubble can capture the electrons at the base of the bubble and accelerate them with a narrow energy spread.The quality of the accelerated electrons is mainly determined by the evolution of the bubble structure. Recently, there have been several theoretical[22,23] and experimental[24] investigations to study the influence of the bubble evolution on the wake field structure and hence on the quality of the electron beam.It has been shown that in the fully relativistic regime in which the normalized vector potential of laser a 0 = eE 0/m e cω 0 approaches 1 (where E 0 and ω0 are the peak electric field and the frequency of the laser), the interaction of the laser with the under-dense plasma can lead to several nonlinear processes such as laser self-steepening.[25] In laser self-steepening, the peak region of the pulse with high-intensity moves faster than those with low intensity at the pulse head. This leads to optical shock formation and then a nonlinear wake is excited. As a result,the plasma wavelength elongates and uninterrupted self-injection follows.[26–28] The laser pulse is depleted due to the excitation of a plasma wave. For a situation where the laser is ultra-intense (a 0 ≫ 1), the pump deletion occurs at a narrow region in front of the pulse corresponding to a few cycles of the laser front.[29] A consequence of the localized pulse depletion is induction of the transverse oscillations in the bubble sheath leading to multi-injection, a large energy spread and collective transverse oscillation of the electron beams.[30] Therefore, it is important to control these instabilities to achieve high-quality electron beams. In this work the interaction of a chirped laser pulse with the under-dense plasma is studied via two-dimensional (2D) particle-in-cell (PIC) simulations. The aim of this work is to propose a new approach to suppress the induced transverse oscillations in the bubble structure at ultra-relativistic regimes (a 0 ≈ 10) using the frequency-chirped laser pulse. Based on this technique, a considerable difference in pulse depletion process is observed for positively and negatively chirped laser pulses. This difference can be used to tune the bubble structure and hence, the quality of the injected bunch in the nonlinear bubble regime.
The interaction of the short-pulse and the ultra-high intense lasers (I > 1019 W/cm2) with the undersense plasma presents different features compared to moderately high intensities (I < 1018 W/cm2). At moderately high intensity, the nonlinear instabilities like relativistic self-focusing,[31] relativistic self-phase modulation,[32] Raman backward and forward scattering,[33] and envelope self-modulation[34] cause the laser pulse to be absorbed and scattered in a distance of the order of a Rayleigh length. At ultra-high intensities, due to relativistic effects,[35–38] the growth rate for the above-mentioned instabilities decreases. This leads to the depletion of only the leading edge of the pulse and the main body of the pulse undergoes little modification. Therefore, the laser pulse eventually evolves to a state in which the leading edge becomes a step function. The phase and the group velocity of the laser in a dispersive medium such as plasma are not equal. Therefore, propagation of a laser pulse through plasma induces a phase shift between the carrier wave and the envelope known as the carrier–envelope phase (CEP). The time variation of the electric field for extremely short laser pulses of few-oscillations depends on the carrier–envelope phase. The localized depletion of a laser pulse at ultra-high intensities causes the varying electric field of the laser at the front of the depleted pulse to act like a few-cycle pulse[39,40] in which the asymmetric transverse ponderomotive force leads to the occurrence of the transverse oscillations in the bubble structure.[41] To stabilize the bubble shape, the depletion of the pulse leading edge must be mitigated in order to avoid the effect of the carrier phase shift on the transverse ponderomotive force. Since the depletion velocity of the pulse, i.e., 
Here the electric field amplitude of the laser pulse is defined as E 0 which is a constant value. The local frequency of the linearly chirped pulse, the longitudinal laser length, and the laser beam waist are denoted by ω (ξ) = (1 – bξ), σ x and σ y respectively. Here, b > 0 (b < 0) denotes the dimensionless chirp parameter for the positively (negatively) chirped pulse and ξ = [(x – ct) ω0/c] is the dimensionless delayed time in which c, m e, ω0 and e are the speed of light in vacuum, the plasma electron mass, the local frequency in the center of the pulse, and the absolute charge of the plasma electron, respectively. Also, t and x represent the time and spatial coordinates, respectively. In this work the laser beam waist, the longitudinal laser length, and the normalized incident laser amplitude are set equal to σy = 8 µm, σx = 10 µm, and a0 = eE 0/m e cω0 = 10 respectively.
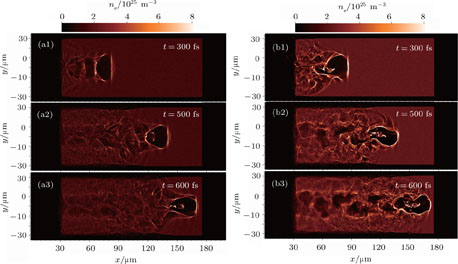
The bubble structure at the three different instances during the propagation of the laser pulse through the under-dense plasma are shown in Fig.
As is clear from Fig.
As shown in Figs.
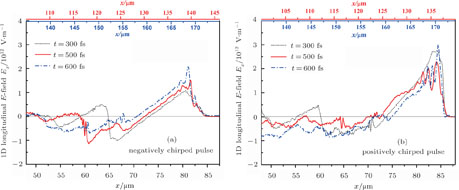
In this situation the front of the pulse is approximately converted to a one-cycle profile. Once the leading edge of the pulse erodes, the bubble structure becomes susceptible to transverse instabilities. In fact, considering the plasma as a dispersive medium, due to the induced phase shift between the carrier waves and the pulse envelope, the role of the time average of the laser field at the front of the depleted pulse becomes dominant on the intensity envelope of the pulse in laser–plasma interactions. Therefore, changing the field direction at the pulse front, as it is depicted by the red and blue arrows in Fig.
As can be seen for the negatively chirped pulse the symmetric structure of the moving bubble remains stable with time (Figs.
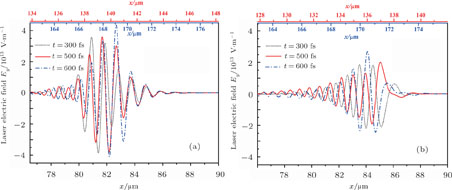
In fact, with the higher frequencies located in front of the pulse, the plasma transparency increases at the leading part of the pulse that results in the excitation of a small density spike (Fig.
As a result, the pulse depletion rate at the leading edge of the negatively chirped (positively chirped) pulse decreases (increases) and thus, the carrier phase shift becomes negligible (significant) in the leading edge of the pulse as depicted in Fig.
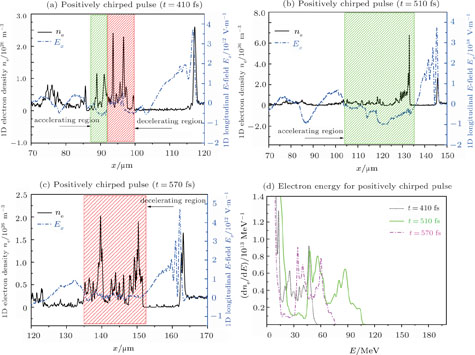
The longitudinal electric field together with the plasma density are shown in Figs.
However, as can be clearly seen in Figs.
By comparing the energy spectrum of the electrons for the negatively and the positively chirped pulse (Figs.
In the nonlinear bubble regime, the transverse oscillations of the cavity structure as a result of the depletion of the pulse leading edge can be controlled by applying the chirped laser pulses. The simulation results show that by locating the higher frequencies in front of the pulse, the pulse depletion process is postponed, thus the cavity structure stays stable for a longer time and a single electron bunch with a higher energy can be generated. In the case in which the lower frequencies are located at the front of the pulse, the pulse depletion speeds up, thus the transverse instability of the bubble appears in an earlier stage of laser plasma interaction. The unstable bubble results in the accelerating phase of the wake field being turned into the decelerating phase, frequently. As a consequence the energy loss of the injected electrons causes the generation of the electron bunches with lower mean energy. Therefore, the utilizations of the chirped laser pulse provides a method to control the quality of the generated bunch in the nonlinear bubble regime.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] |