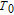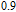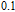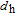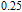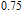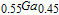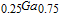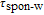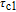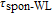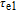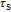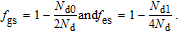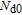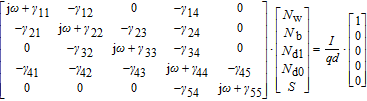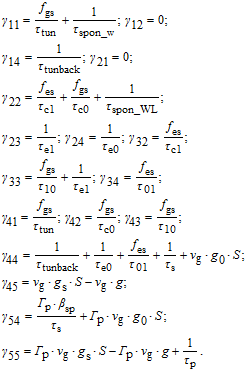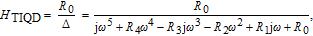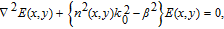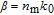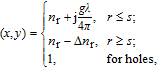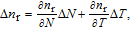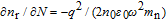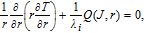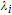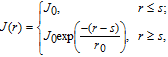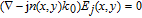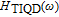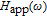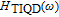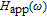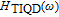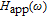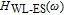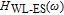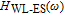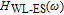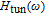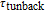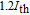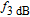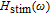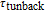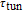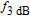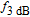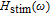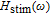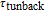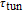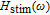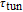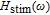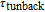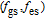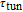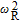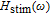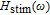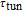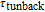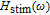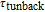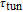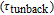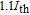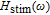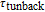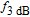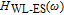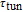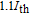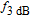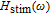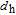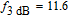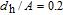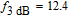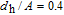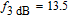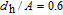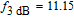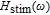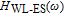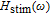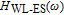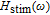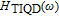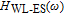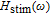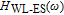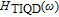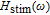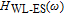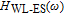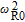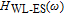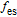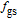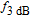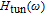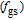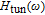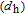Simplified modeling of frequency behavior in photonic crystal vertical cavity surface emitting laser with tunnel injection quantum dot in active region
1. IntroductionSemiconductor quantum dot (QD) lasers including edge emitting and vertical cavity surface emitting lasers have more significant advantages than other lasers like bulk, quantum well, and wire in some characteristics, such as large differential gain,[1,2] low threshold current,[3,4] temperature insensitivity of the threshold current,[5,6] and high output power[7] because of their delta shape discrete density of states.
However, their carrier dynamic operations at high speed are not satisfactory enough, due to a phonon bottleneck appearing in electrons and holes capturing process[8,9] leading to a hot-carrier problem in QD lasers. The effect of hot carrier followed by the gain compression triggers the reduction of the differential gain.[10] Thus the resonance frequency is limited by the maximum modal gain and gain compression effects. Therefore the maximum modulation bandwidth, which is dependent on the resonance frequency and damping factor, decreases. So, the hot-carrier problem is an important reason for the disability of QD lasers to operate at high frequencies. Also, it is demonstrated that finite carrier capture, finite relaxation time, and Pauli blocking factors limit the maximum modulation bandwidth.[11]
To solve the problem one of the solutions is to use the tunneling injection method (TI). At first, the tunneling injection method is performed in active region for quantum well semiconductor lasers. By tunneling “cold” electrons directly into the lasing states of GaAs- and InP-based quantum well lasers from an adjacent injector layer, the performance characteristics including enhanced modulation bandwidth and higher characteristic temperature (
 ), the reduced Auger recombination and the reduced chirp are both demonstrated in Refs. [12]–[14]. Also, the TI scheme has been implemented in quantum well vertical-cavity surface-emitting lasers (QW-VCSELs).[15]
), the reduced Auger recombination and the reduced chirp are both demonstrated in Refs. [12]–[14]. Also, the TI scheme has been implemented in quantum well vertical-cavity surface-emitting lasers (QW-VCSELs).[15]
The technique of TI is applied to QD lasers, too. In tunneling injection quantum dot structure, electrons are introduced directly or in the phonon-assisted way into the lasing states of dots. Thus, the probabilities of electrons existing in the wetting layer and excited state, decrease. Then, the effects of hot carrier and gain compression are reduced and the differential gain increases.
By using the tunneling injection technique, small signal modulation is measured at frequencies more than 20 GHz.[16] In tunneling injection structure, in addition to the effect of carrier capture and relaxation, the tunneling rate also affects the resonance frequency and damping factor. So, with a smaller tunneling time, the performance of laser is increased. It is shown in Ref. [17] that with different thickness values of the barrier, the tunneling time can be adjusted.
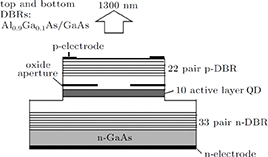
In this paper, a numerical model is presented to simulate the behavior of tunneling injection quantum dot VCSEL by using the method described in Ref. [11]. VCSELs are proven to have some unique properties such as high reliability, high internal efficiency, low divergence angle, simple fabrication process into twodimensional arrays.[18]
In our model, the bandwidths of modulation transfer functions associated with different levels of energy in dot and injector well are obtained. In this manner, the effect of tunnel injection on the resonance frequency and also on the bandwidth of modulation transfer function of TIQD laser is presented. Generally, the modulation transfer function components in the wetting layer (WL) and excited state (ES) limit the total bandwidth. However, in TIQD structure, modulation transfer function component related to tunneling process from injector well into QDs ground state experiences a high bandwidth leading to the increase of the entire modulation bandwidth. We base our study on the TI-QD-VCSEL model by a hetero-structure in active region and 1.3-μm QD-VCSEL which is based on experimental work in Refs. [19] and [20]. Also, in order to investigate the effect of photonic crystal (PhC) waveguide on the frequency behavior of laser, we consider a model of two-dimensional photonic crystal (PhC) waveguide embedded in entire VCSEL. The dynamic response of VCSEL varies with the structure and dimension of the laser cavity.[21] Oxide aperture depth and diameter as well as the characteristics of photonic crystal structure such as air holes diameter and PhC lattice constant are important parameters which affect the frequency response of VCSELs due to some properties such as spatial hole burning and self-heating effect. In order to take into account all phenomena of the laser, spatial hole burning (SHB) due to stimulated recombination of carriers and thermal lensing (TL) a result of the self-heating effect and transverse mode competition needs to be considered. The coupled optical field, diffusion, and thermal conduction equations are solved by using the algorithm of the self-consistent calculation which is described in Ref. [22].
The rest of this paper is organized as follows. In Sections 2 and 3, we investigate the dynamic carrier of the laser and the factors affecting the resonance frequency and damping factor and derive a new modulation transfer function similar to that in Ref. [11] through a small signal analysis of differential rate equations. In Section 4, the numerical results of tunneling injection are presented and by comparing with the conventional quantum dot, the origin of improvement of frequency response in TIQD structure, is investigated.
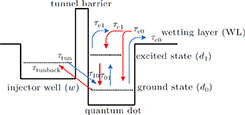
3. Numerical model descriptionIn the active region, we consider a model similar to the tunnel injection quantum dot active region structure in Ref. [16] whose sketch is shown in Fig. 2 consisting of the In
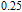 Ga
Ga
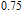 As injector well, an Al
As injector well, an Al
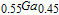 As tunnel barrier, and three coupled In
As tunnel barrier, and three coupled In
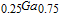 As QD layers. In order to efficiently realize the phonon assisted tunneling from the injector layer to the dots, the conduction band states of the injector layer with the bound states in QDs are aligned.[16] In our model, it is assumed that the active region consists of only one QD ensemble including two energy levels: a ground state (GS) with a two-fold degenerate and an excited state (ES) with a four-fold degeneration. The system is assumed to consist of excitonic energy states, while QDs are always neutral, and electrons and holes are treated as electron–hole pairs.
As QD layers. In order to efficiently realize the phonon assisted tunneling from the injector layer to the dots, the conduction band states of the injector layer with the bound states in QDs are aligned.[16] In our model, it is assumed that the active region consists of only one QD ensemble including two energy levels: a ground state (GS) with a two-fold degenerate and an excited state (ES) with a four-fold degeneration. The system is assumed to consist of excitonic energy states, while QDs are always neutral, and electrons and holes are treated as electron–hole pairs.
According to the carrier dynamics in the conduction band shown in Fig. 2, the external carriers are first injected into SCH and then into the injector well. Some of the carriers are then either introduced into the QD ground state directly or by phonon-assisted tunneling, and some of them participate in spontaneous emission processes, with a rate time of
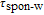 . Once in the WL, carriers are captured into the ES within time
. Once in the WL, carriers are captured into the ES within time
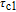 and directly into the GS within time
and directly into the GS within time
 or participate in spontaneous emission processes with a rate time of
or participate in spontaneous emission processes with a rate time of
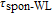 . Carriers on the excited state are relaxed into the GS within time
. Carriers on the excited state are relaxed into the GS within time
 and on the other hand, they are also thermally reemitted from the ES to the WL with a
and on the other hand, they are also thermally reemitted from the ES to the WL with a
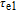 which is governed by the Fermi distribution for the quasi-thermal equilibrium without external excitation.[24] Carriers on the ground state level have a similar dynamic behavior to ES, while some of them recombine spontaneously with a spontaneous time
which is governed by the Fermi distribution for the quasi-thermal equilibrium without external excitation.[24] Carriers on the ground state level have a similar dynamic behavior to ES, while some of them recombine spontaneously with a spontaneous time
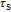 . Most carriers reside in the injector well and in the wetting layer at room temperature, so the Auger recombination has not been explicitly considered in ES and GS levels.[16] In our model, the stimulated emission from the GS is just taken into account and occurs when the threshold is reached. Following the sketch in Fig. 2, the carrier dynamics defined by a set of rate equations given in Ref. [16] is as follows:
. Most carriers reside in the injector well and in the wetting layer at room temperature, so the Auger recombination has not been explicitly considered in ES and GS levels.[16] In our model, the stimulated emission from the GS is just taken into account and occurs when the threshold is reached. Following the sketch in Fig. 2, the carrier dynamics defined by a set of rate equations given in Ref. [16] is as follows:
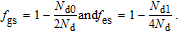 | (2) |
The optical gain in the cavity as a function of
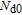
and
S is given by
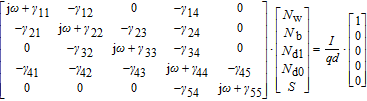 | (3) |
with
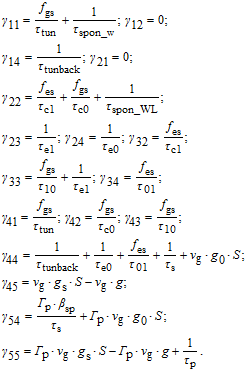 | (5) |
As given in Ref. [
11], one can extract a modulation transfer function as
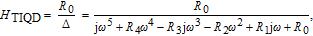 | (6) |
where
Δ is the determinant of the matrix symbol and the
R parameters can be obtained from the coefficients of the matrix.
Now, we define the relaxation resonance frequency and damping factor for the lasing level versus coefficients of matrix as
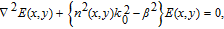 | (13) |
where
E(
x, y) is the transverse electrical field pattern,
n(
x, y) is the refractive index pattern,

is vacuum preparation constant,
λ is the wavelength of optical wave,
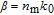
is the mode propagation constant, and
nn
m is the mode effective index. The transverse distribution of the refractive index can be defined as follows:
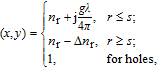 | (14) |
where
n
r is the refractive index of passive GaAs region,
g is described in Eq. (
3) and depends on radial profile of carrier density, and
s is the radius of the oxide aperture. Taking into account the spatial hole burning (SHB) and thermal lensing (TL) effects, we consider the contributions of carrier and temperature distributions to changes of the refractive index
Δn
r,
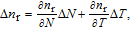 | (15) |
with
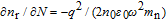
, where
n
0 is the refractive index of active region, and
m
n is the effective mass of the electron.
For GaAs,
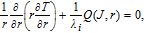 | (16) |
where
T is the temperature,
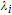
is the effective thermal conductivity of the laser cavity,
r denotes radius,
Q(
J, r) is the density of the total heat energy generated in the laser including Joule heating in DBR layers, absorption of spontaneous emission, and nonradiative recombination in the active region. We calculate
Q(
J, r) by following the approach in Ref. [
23]. The most significant current spreading in the VCSEL takes place in the current region. To simplify the calculation, we consider the following approximation:
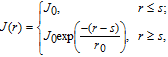 | (17) |
where
J
0 is the injected current density and
r
0 is a constant which determines the extent of the current spreading.
4. Results and discussionAt first, we numerically solve the steady state of the coupled equations (13)–(17) by using the algorithm of the self-consistent calculation. Diffusion equations of TIQD structure are created from the rate equation with adding ∇2
N
w and ∇2
N
WL terms in steady state and is solved with the nonlinear Newton method for determining the radial profile of carrier concentration. Thermal equation is solved by the finite difference method with Dirichlet boundary conditions. Field equation is solved by the finite difference method with absorbing boundary conditions accordingly to
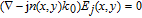 . Then, the frequency behavior of laser is studied by using an analytical approximation of the model which has been discussed in the previous section.
. Then, the frequency behavior of laser is studied by using an analytical approximation of the model which has been discussed in the previous section.
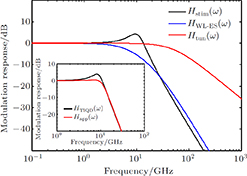
The components of approximate solution
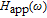 presented in Eqs. (10a)–(10d) are shown in Fig. 3. The inset presents the precise modulation transfer function
presented in Eqs. (10a)–(10d) are shown in Fig. 3. The inset presents the precise modulation transfer function
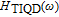 given by Eq. (6) and the approximate solution
given by Eq. (6) and the approximate solution
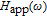 which shows that the
which shows that the
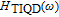 and
and
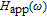 curves are approximately close to each other.
curves are approximately close to each other.
It can be seen that the behavior of response of
 to frequency is similar to that of quantum well structure.[11] While, among the components of
to frequency is similar to that of quantum well structure.[11] While, among the components of
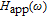 ,
,
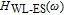 is the underlying limitation to the enhancement of the total modulation bandwidth, because the modulation bandwidth of
is the underlying limitation to the enhancement of the total modulation bandwidth, because the modulation bandwidth of
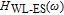 is much smaller than others’. Of course, in TIQD structure, the carrier dynamics in the inter-band of dots has no significant influence on
is much smaller than others’. Of course, in TIQD structure, the carrier dynamics in the inter-band of dots has no significant influence on
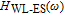 , while in CQD, the finite carrier capture time and finite carrier relaxation time are the effective physical limitations to the enhancement of
, while in CQD, the finite carrier capture time and finite carrier relaxation time are the effective physical limitations to the enhancement of
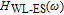 modulation bandwidth.[11] This is the evidence for the advantage of using a tunnel injection quantum dot compared with using the conventional QD. In addition,
modulation bandwidth.[11] This is the evidence for the advantage of using a tunnel injection quantum dot compared with using the conventional QD. In addition,
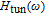 has the highest bandwidth, which leads to the increase of the total modulation bandwidth. Given that this component is related to the tunneling time, the behavior of modulation will be improved for shorter tunneling time.
has the highest bandwidth, which leads to the increase of the total modulation bandwidth. Given that this component is related to the tunneling time, the behavior of modulation will be improved for shorter tunneling time.
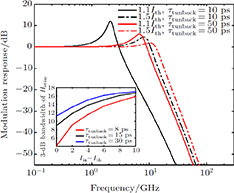
Generally, due to tunnelling injection, total frequency behaviour of laser has less dependence on inter-band dynamic of QD. However, the back tunnelling time from GS to the injector well is a more important parameter for determining the 3-dB bandwidth of total transfer function by its direct influence on the bandwidth of
 . Figure 4 shows frequency responses of the laser for four different values of back tunnelling time from GS to the injector well (
. Figure 4 shows frequency responses of the laser for four different values of back tunnelling time from GS to the injector well (
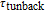 ) at
) at
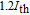 , while the inset shows
, while the inset shows
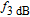 variations of
variations of
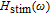 with
with
 for differentvalues of carrier tunnelling time (
for differentvalues of carrier tunnelling time (
 ). By comparing these results, it can be seen that by increasing the
). By comparing these results, it can be seen that by increasing the
 ,
,
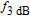 of total transfer function is increased due to high increment of
of total transfer function is increased due to high increment of
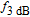 of
of
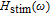 as shown in the inset. As depicted, in the case of low back tunnelling time, the changes of 3-dB bandwidth of
as shown in the inset. As depicted, in the case of low back tunnelling time, the changes of 3-dB bandwidth of
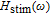 is intense, but in the case of high value of back tunnelling time, 3-dB bandwidth of
is intense, but in the case of high value of back tunnelling time, 3-dB bandwidth of
 changes slower so that, forshort tunneling time, it is approximately independent of
changes slower so that, forshort tunneling time, it is approximately independent of
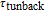 . Also, with small back tunnelling time,
. Also, with small back tunnelling time,
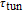 has an indirect influence on the bandwidth of lasing transfer function component
has an indirect influence on the bandwidth of lasing transfer function component
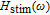 due to generated photon. While, in the case of large back tunnelling time, the effect of
due to generated photon. While, in the case of large back tunnelling time, the effect of
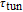 on the bandwidth of
on the bandwidth of
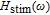 is very weak. Because, by increasing
is very weak. Because, by increasing
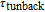 , there will be no back tunneling process approximately toward injector well. So, carrier densities at the ES and the GS levels of dots as well as the Pauli blocking factors
, there will be no back tunneling process approximately toward injector well. So, carrier densities at the ES and the GS levels of dots as well as the Pauli blocking factors
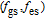 have small changes due to photon density created in the cavity and will almost be less dependent on the value of
have small changes due to photon density created in the cavity and will almost be less dependent on the value of
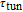 . According to the expressions of
. According to the expressions of
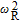 and Γ in
and Γ in
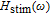 and their dependence on photon density, 3-dB bandwidth of
and their dependence on photon density, 3-dB bandwidth of
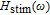 is less impressible to
is less impressible to
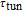 for large value of
for large value of
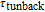 .
.
The frequency response of the laser is plotted in Fig. 5 for two different values of back tunnelling time
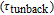 at
at
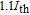 and
and
 . It can be concluded that for a large value of
. It can be concluded that for a large value of
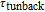 , the dependence of 3-dB bandwidth on the bias current is not so strong. The inset shows laser 3-dB bandwidth changes of
, the dependence of 3-dB bandwidth on the bias current is not so strong. The inset shows laser 3-dB bandwidth changes of
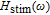 with bias current for three different values of
with bias current for three different values of
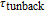 . It is observed that by increasing
. It is observed that by increasing
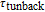 , the dependence of
, the dependence of
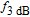 on the bias current decreases with the increase of current. It should be noted that the bandwidth of
on the bias current decreases with the increase of current. It should be noted that the bandwidth of
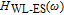 is not dependent on
is not dependent on
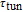 , nor
, nor
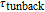 . But, the tunnelling time
. But, the tunnelling time
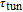 affects the bandwidth of
affects the bandwidth of
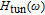 strongly.
strongly.
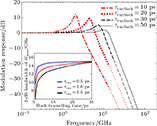
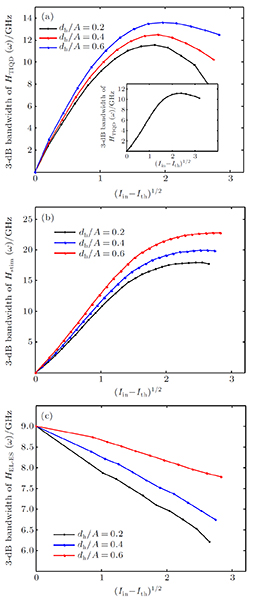
Now, in order to investigate the effect of photonic crystal (PhC) waveguide on the frequency behavior of laser, the 3-dB bandwidth of transfer function of TIQD-PhC-VCSEL and its components are plotted in Figs. 6(a)–6(c) as a function of injected current for various values of air hole diameter (
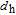 ) with a fixed value of PhC lattice constant (A = 2 μm). Oxide aperture diameter (s) and spreading current (r) are 10 μm and 1 μm, respectively. The threshold currents are obtained to be 3.2 mA, 4.6 mA, and 59 mA. The 3-dB bandwidth of transfer function of TIQD-VCSEL with the same structure is shown in the inset of Fig. 6(a). As can be seen from Fig. 6(a) the bandwidth of
) with a fixed value of PhC lattice constant (A = 2 μm). Oxide aperture diameter (s) and spreading current (r) are 10 μm and 1 μm, respectively. The threshold currents are obtained to be 3.2 mA, 4.6 mA, and 59 mA. The 3-dB bandwidth of transfer function of TIQD-VCSEL with the same structure is shown in the inset of Fig. 6(a). As can be seen from Fig. 6(a) the bandwidth of
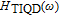 increases with increasing bias current and is saturated for high values. The occurrence of rollover of the modulation response at the high bias current is due to both self-heating effect (with more effectiveness) and the emergence of high-order modes (with less effectiveness). The rollovers are observed at
increases with increasing bias current and is saturated for high values. The occurrence of rollover of the modulation response at the high bias current is due to both self-heating effect (with more effectiveness) and the emergence of high-order modes (with less effectiveness). The rollovers are observed at
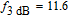 GHz for
GHz for
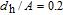 ,
,
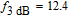 GHz for
GHz for
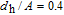 , and
, and
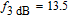 GHz for
GHz for
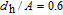 , respectively. While in TIQD-VCSEL without photonic crystal structure the rollover is at
, respectively. While in TIQD-VCSEL without photonic crystal structure the rollover is at
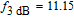 GHz at 3.4-mA threshold current. Relaxation rate in QD will decrease as a result of phonon bottleneck caused by increasing temperature in the active region. For larger air hole diameter, the bandwidth increases more intensely at low bias currents, and is saturated later. Since the air holes diameter has a significant influence on the reduction of thermal lensing and spatial hole burning effect. So, with its increase, the temperature decreases and the gain increases in the center of the active region. In TIQD structures, this rollover is less than that in conventional quantum dot structure by solving the phonon bottleneck problem. In order to further analyse the variations of 3-dB bandwidth of
GHz at 3.4-mA threshold current. Relaxation rate in QD will decrease as a result of phonon bottleneck caused by increasing temperature in the active region. For larger air hole diameter, the bandwidth increases more intensely at low bias currents, and is saturated later. Since the air holes diameter has a significant influence on the reduction of thermal lensing and spatial hole burning effect. So, with its increase, the temperature decreases and the gain increases in the center of the active region. In TIQD structures, this rollover is less than that in conventional quantum dot structure by solving the phonon bottleneck problem. In order to further analyse the variations of 3-dB bandwidth of
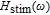 and
and
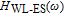 versus bias current are shown in Figs. 6(b)–6(c). The presented results point out that 3-dB bandwidth of
versus bias current are shown in Figs. 6(b)–6(c). The presented results point out that 3-dB bandwidth of
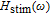 increases with the increase of current, while
increases with the increase of current, while
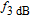 of
of
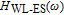 is reduced, slightly. The effect of air-hole diameter on the 3-dB bandwidth of
is reduced, slightly. The effect of air-hole diameter on the 3-dB bandwidth of
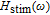 is almost similar to that of
is almost similar to that of
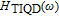 . The reduction of 3-dB bandwidth of
. The reduction of 3-dB bandwidth of
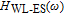 is more intense for smaller air-hole diameter. Based on the variations of
is more intense for smaller air-hole diameter. Based on the variations of
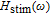 and
and
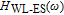 as well as
as well as
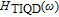 , in the case of low bias current the effect of increase of 3-dB bandwidth of
, in the case of low bias current the effect of increase of 3-dB bandwidth of
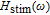 is dominant over the effect of reduction of 3-dB bandwidth of
is dominant over the effect of reduction of 3-dB bandwidth of
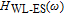 , while frequency behavior of
, while frequency behavior of
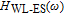 will be predominant in the case of high bias current. On the other hand, carrier dynamic behaviors in wetting layer and excited state levels are more influenced by spatial hole burning and thermal effects. In the TIQD structures, current dependence of
will be predominant in the case of high bias current. On the other hand, carrier dynamic behaviors in wetting layer and excited state levels are more influenced by spatial hole burning and thermal effects. In the TIQD structures, current dependence of
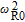 and Γ are negligible despite CQD decreasing linearly with the increase of current.[11] Thus, the limitation to the bandwidth of
and Γ are negligible despite CQD decreasing linearly with the increase of current.[11] Thus, the limitation to the bandwidth of
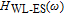 does not restrict the total modulation bandwidth with the increase of current. This is attributed to the current being not dependent on Pauli blocking factor
does not restrict the total modulation bandwidth with the increase of current. This is attributed to the current being not dependent on Pauli blocking factor
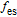 nor
nor
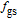 . The
. The
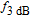 of
of
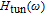 is approximately independent of the current (not shown here). Based on Eqs. (5) and (10d), the results indicate that the constant Pauli blocking factor in ground state
is approximately independent of the current (not shown here). Based on Eqs. (5) and (10d), the results indicate that the constant Pauli blocking factor in ground state
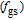 is effective to small reduction of 3-dB bandwidth of
is effective to small reduction of 3-dB bandwidth of
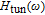 in TIQD when increasing the current.
in TIQD when increasing the current.
5. ConclusionsThrough the analysis of modulation transfer function, the characteristics of the photonic crystal tunneling injection quantum dot vertical cavity surface emitting lasers (PhC-TIQD-VCSEL) are studied. Based on the rate equations describing the carrier dynamics, the modulation transfer function is obtained and divided into the components related to the energy levels in the dot and the injector well. Numerical investigation clarifies the effect of the tunneling injection on the enhancement of the modulation response. The results show that the carrier back-tunneling time from the dot ground state into the injector well is the most effective parameter to determine the frequency response of TIQD-VCSEL. The frequency behaviors of WL-ES and GS levels are also affected by the variations of the structure and dimension of laser cavity as well as air-hole diameter and lattice constant of photonic crystal structure due to some nonlinear effects such as spatial hole burning and thermal lensing effects. However the component of tunneling process is almost independent of them.