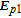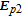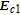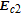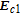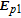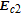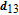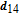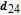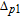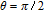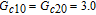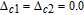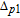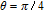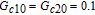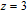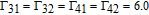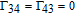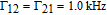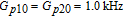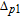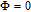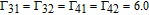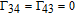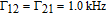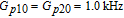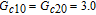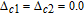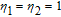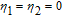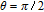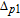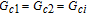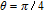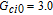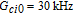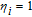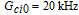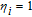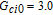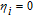† Corresponding author. E-mail:
We have studied the probe gain via a double-Λ atomic system with a pair of closely lying lower levels in the presence of two probe and two coherent pump fields. The inversionless gain can be realized by using nondegenerate four-wave mixing under the condition of spontaneously generated coherence (SGC) owing to near-degenerate lower levels. Note that by using SGC, two probe fields can be amplified with more remarkable amplitudes, and the gain spectra of an extremely narrow linewidth can be obtained. Last but not least, our results show that the probe gain is quite sensitive to relative phases due to the SGC presence which allows one to modulate the gain spectra periodically by phase modulation, and can also be influenced by all laser field intensities and frequencies, and the angles between dipole elements.
In recent years, lasing without population inversion (LWI) has been demonstrated experimentally and theoretically, which provides us with an important and interesting alternative[1–8] depending on the incoherent pumping process. Thus the high-frequency laser (i.e., the ultraviolet or x-ray range) can be realized which is impractical in conventional lasering with population inversion. The essence of LWI achieved with applied fields attributed to either inversion between dressed states or coherence among these states.[9–12] Due to the multiple potential applications of LWI, i.e., from ultrahigh-sensitive magnetometers to the generation of giant pulses of laser light and from cooling to isotope separation,[13–15] various schemes to realize inversionless gain have been proposed and attracted extensive attention.[16, 17] Then, some factors have been considered in the LWI scheme, such as the phase of external fields which can modulate the probe gain periodically.[18–21] Besides, the effect of spontaneously generated coherence (SGC) depending on nonorthogonality of dipole matrix elements[24–26] has been discussed in the systems of light amplification without population inversion as shown in Refs. [18]–[23]. In those systems, SGC may destroy the dark state for achieving laser-gain, as the coherence process of spontaneous emission arises from two interference channels (either from two closely lying excited levels to a common ground level or from a common excited level to two closely lying ground levels.[27, 28])
In this article, we study inversionless probe gain in a coherently driven four-level double-Λ atomic system. Being distinct from previous schemes depending on an incoherent pump to destroy dark states, our scheme’s probe fields are amplified by common contributions of the resonant four-wave mixing (FWM) process and the electromagnetically induced transparency (EIT) effect. The resonant FWM process can be used to amplify probe fields and the EIT results in the reduction of probe absorption.[29–37] Moreover, the atomic system in our study has two closely lying lower levels, so SGC should be taken into account. It is interesting that the probe fields can be enhanced approximately 2500 times owing to the coherence arising from the spontaneous emission. Meanwhile, a narrow gain spectral linewidth can be obtained by decreasing the coherent pump field Rabi frequencies. An obvious advantage of the high and narrow gain spectral line is that it can be used to improve the measuring accuracy. Besides, we further study the probe gain modulation by adjusting the relative phase between applied fields. Our numerical results show that the probe gain is sensitive to the phase, and restricted by the angle between dipole elements.
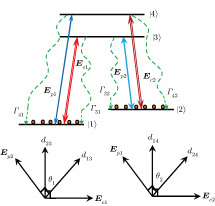
We consider a four-level double-Λ atomic system of two far-spaced upper levels 
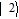
The electric dipole-allowed transitions 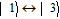

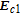
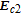

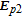
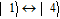
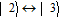
 | (1) |
Then, by substituting 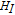
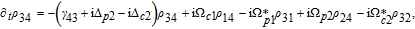 | (2) |
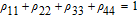
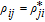
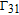
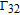
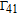
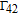
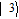
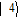
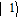
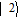
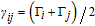
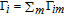
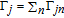
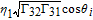
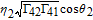
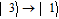

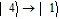
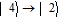
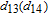
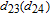
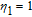
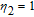
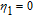
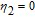
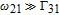
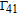
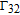
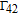
By taking into account the field phases required by SGC, we rewrite the complex Rabi frequencies as 
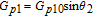
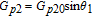
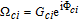
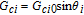
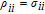
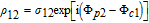
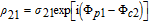
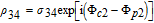
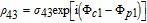
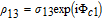
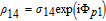
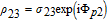
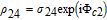
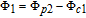
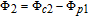
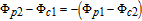
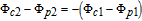
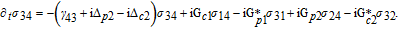 | (3) |
Note that equations (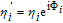
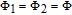
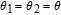
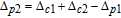
With EIT and nondegenerate four-wave mixing nonlinearities, the inversionless gain has been discussed recently,[38] where the probe fields can transmit through the medium due to the laser induced quantum interference, and amplified in the process of resonant nondegenerate four-wave mixing, however, the gain amplitude is often small. Here, we find that with considering SGC, it is more interesting that the probe fields can be amplified with a much larger amplitude due to the interference between spontaneous emission channels via the four-wave mixing. Meanwhile, we can achieve inversionless gain because most atomic populations distribute on ground levels 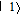

The probe field susceptibility is
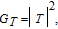 | (4) |
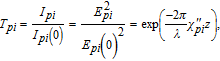 | (5) |
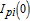
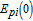

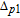
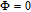
When 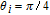
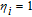
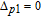
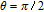
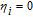
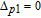
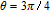
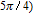

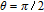
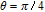

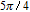
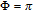
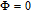

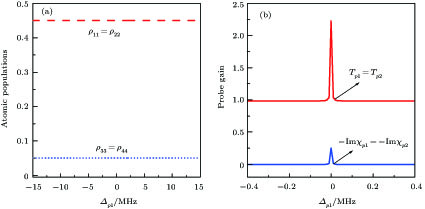
However, the gain amplitude may be enhanced with increasing the coherent field intensity. In Fig. 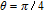
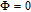
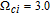
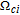
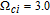
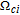
Figure 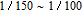
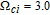
In general, phase dependence is expected for a closed-loop excitation structure where pairs of modes interact through a common spin coherence.[41–45] In the single Λ system, there is no influence of the relative phase, except for the existence of SGC.[46] So there is no doubt that in our regime the probe gain is sensitive to the relative phase 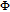

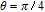
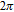
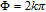
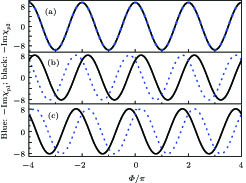 | Fig. 5. (color online) Probe gain spectra versus relative phase 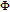
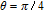
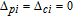
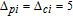
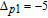
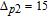
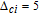
|
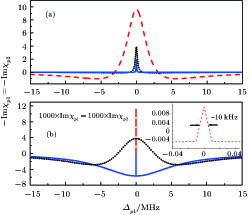
As shown in Fig. 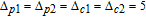
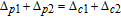
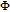
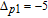

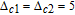
In order to examine the relationship between θ and 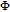
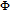
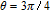
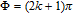
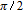
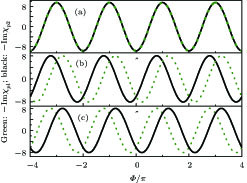 | Fig. 6. (color online) Probe gain spectra versus the phase 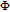
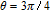
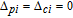

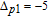
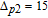
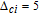
|
Our work is based on the theoretical model which provides meaningful and surprising results. The probe gains can be improved largely by considering SGC, and a narrow probe spectrum can be obtained by reducing the Rabi frequency of coupling fields. To the best of our knowledge, the linewidth of the probe spectrum can be modulated easily in the region between 1.5 MHz and 15 MHz in the existing experimental level.[47–49] Moreover, in experiment, the SGC is rather difficult to be achieved in a real atomic system. This rigorous condition can be realized in charged quantum dots and the atomic system with atoms placed near a metallic nanostructure or managed in the dressed-state picture.[50–52] For considering the experimental realization, the two close levels can be chosen as well separated Zeeman levels which belong to different hyperfine states of our model.[53]
In summary, we elaborately studied the inversionless gain with nondegenerate FWM linearities under the condition of EIT and SGC. We find that the two probe fields are simultaneously amplified with the same extent in a spectral range around 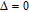

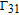
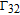
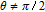
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] |