Cite this Article
Ding Zong-Ling, Sun Zhao-Qi, Sun Jin, Li Guang, Meng Fan-Ming, Wu Ming-Zai, Ma Yong-Qing, Cheng Long-Jiu, Chen Xiao-Shuang. The inelastic electron tunneling spectroscopy of edge-modified graphene nanoribbon-based molecular devices. Chinese Physics B, 2017, 26(2): 023103  
Permissions
The inelastic electron tunneling spectroscopy of edge-modified graphene nanoribbon-based molecular devices
Ding Zong-Ling1, †, Sun Zhao-Qi1, Sun Jin1, Li Guang1, Meng Fan-Ming1, Wu Ming-Zai1, Ma Yong-Qing1, Cheng Long-Jiu2, Chen Xiao-Shuang3
School of Physics and Material Science, Anhui University, Hefei 230601, China
College of Chemistry and Chemical Engineering, Anhui University, Hefei 230601, China
National Laboratory of Infrared Physics, Shanghai Institute for Technical Physics, Chinese Academy of Sciences, Shanghai 230083, China

 

† Corresponding author. E-mail: zlding@ahu.edu.cn

Abstract

The inelastic electron tunneling spectroscopy (IETS) of four edge-modified finite-size grapheme nanoribbon (GNR)-based molecular devices has been studied by using the density functional theory and Green‘s function method. The effects of atomic structures and connection types on inelastic transport properties of the junctions have been studied. The IETS is sensitive to the electrode connection types and modification types. Comparing with the pure hydrogen edge passivation systems, we conclude that the IETS for the lower energy region increases obviously when using donor–acceptor functional groups as the edge modification types of the central scattering area. When using donor–acceptor as the electrode connection groups, the intensity of IETS increases several orders of magnitude than that of the pure ones. The effects of temperature on the inelastic electron tunneling spectroscopy also have been discussed. The IETS curves show significant fine structures at lower temperatures. With the increasing of temperature, peak broadening covers many fine structures of the IETS curves. The changes of IETS in the low-frequency region are caused by the introduction of the donor–acceptor groups and the population distribution of thermal particles. The effect of Fermi distribution on the tunneling current is persistent.

PACS: 31.15.es;31.15.at;34.50.–s
Keyword:inelastic electron tunneling spectroscopy;grapheme nanoribbon, edge-modification;molecular junction
1. Introduction

With the miniaturization of materials and device size, carbon-based low-dimensional quantum structure has been more extensively studied both theoretically and experimentally.[1–6] The remarkable structural, electrical and chemical properties of graphene make it one of the important candidates of microelectronics and relative areas.[7–13] Nowadays, one can prepare, characterize and control extremely small scale systems, such as nano-scale molecular devices based on grapheme nanoribbon (GNR) slices.[14–18] The results of our previous work[19] show that the electronic and elastic transport properties of GNR slices are strongly dependent on edge modification types. When used as the molecular core of nano molecular devices, the edge type can tune the carrier distribution of the extended molecules. Furthermore, the connection types of the molecular core and electrodes will have a decisive impact on the contact conductance.[20–23] For small-sized materials and devices, it is difficult to measure and gain the configuration features of the device accurately in experiment. The inelastic electron tunneling spectroscopy (IETS) which is very sensitive to the configuration can give structural information about the molecular junction. Furthermore, the IETS curve can provide a direct access for molecular identification and chemical bonding investigations.[24–30] Thus, investigations of the effects of atomic structure and connection types on inelastic transport properties of edge-modified finite-size GNR-based molecular devices have significant technological implications. In this work, the IETS properties of several edge-modified GNR-based molecular devices have been studied and discussed systematically.

2. Calculation methods and models

Here, four junctions based on finite-sized GNR slices with different edge functional types have been considered as the model systems. The construction process of model systems: based on the two-dimensional graphene structures, we cut to obtain an 8 × 8 rectangular graphene fragment with 8 carbon atoms on the zigzag (ZZ) edges and 8 carbon atoms on the armchair (AC) edges. This 8 × 8 GNR slice is the prototype structure of the molecular core. Then passivation and modification for the dangling bonds of edge carbon atoms have been done. Optimization and relaxation have been down for the molecular core systems. The extended molecules can be established by connecting the molecular core systems with triangle gold clusters. The introductions of a large number of metal atoms in the system often bring magnitude growth of the quantum chemistry calculations. Furthermore, the main and most important IETS information comes from the vibrations of the molecular atoms. Therefore, we choose triangle gold clusters composed of three gold atoms connected with the edge-terminated atoms of the molecular core as the contact geometry of the extended molecules. Two types of modification have been chosen: one is that all of the dangling edge carbon atoms on both ZZ and AC edges have been passivated by hydrogen atoms. The other is that donor–accepter functional groups NH2 and NO2 have been used to substitute the hydrogen atoms of the opposite side of ZZ edge carbon atoms respectively, that is, donor–accepter modifications have been used for the ZZ edges and hydrogen passivation has been used for the AC edges. Then the models have been constructed. For simplicity, the system can be defined as H–H AC/ZZ or A–D AC/ZZ according to the connection type. For example, the notation A–D ZZ indicates a junction constructed by connecting the AC edges of the GNR slice (in which the ZZ edge carbon atoms are modified by NH2–NO2 functional pairs) with Au electrodes, etc. The schematic diagrams of the molecular devices and the atomic structure of the molecular core are shown in Fig. 1. The results of one of our previous works show that edge modification can tune the elastic transport properties of GNR slices-based molecular devices.[19] In this work, we focus on the inelastic scattering process of the junctions.

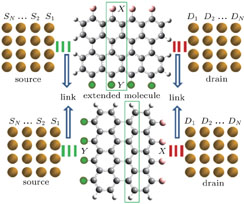Fig. 1. (color online) The Schematic diagrams of the molecular devices and the atomic structure of the molecular core.

The geometric optimization and electronic properties are performed by using the density functional theory in the B3LYP level.[31, 32] In order to obtain more accurate results, we use the 6-31G basis set for light atoms such as carbon, oxygen, nitrogen, and hydrogen and the LanL2DZ basis set for Au atoms. The transport properties are calculated by the quantum chemistry for the molecular electronics (QCME) code.[33–35] The basic theories of the QCME code are the scattering theory and Green’s functional theory. The total current (I) in the junctions include the contributions of elastic (Iel) and inelastic (Iinel) electron scattering from the source to drain electrode. The elastic scattering current is mainly generated from electrons scattering from the molecular orbitals of the extended molecular. When energetic constraints are satisfied, the electron crossing the junction may exchange a definite amount of energy with the molecular nuclear motion, resulting in an inelastic component in the transmission current.[36] It is known that the electron-vibronic coupling can be mainly considered for the extended molecule part. In the adiabatic Born–Oppenheimer approximation, the purely electronic Hamiltonian of the molecular systems can be considered parametrically as dependent on the vibrational normal modes Q. By using a Taylor expansion, the nuclear motion depended wavefunction can be expanded along each vibrational normal mode. The small conductance change induced by the electron-vibronic coupling is commonly measured by the second harmonics of a phase-sensitive detector for the second derivative of the tunneling current d2I/dV2. Since most IETSs are measured at the electronic off-resonant region (where conducting levels are far from the Fermi energy), the adiabatic harmonic approximation can be applied. We can then use the first derivative to represent the vibrational motion part in the wavefunctions. In this case, the total quantum conductance is described as

(1)
where εη is the energy of eigenstate η of the pure electronic Hamiltonian, ωα is the vibrational frequency of vibrational normal modes Qα, and | ѱν (Q)〉 is the vibration wavefunction. According to the device structures, the eigenstate at energy level εη that has been partitioned into three parts runs over the atomic sites in the molecule: the source, drain and extended molecule. The term | Kη〉 is the wave function of the extended molecule subsystem. ψ0η is here the intrinsic electronic wavefunction at the equilibrium position Q0. The parameter z in the Green's function is a complex variable z=Ei+iΓi and Ei is the energy at which the scattering process is observed. Γi is the escape rate.

3. Results and discussions
3.1. The inelastic electron tunneling spectroscopy of edge modified GNRs-based junctions

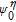
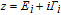
Comparing with the results of elastic scattering, the inelastic scattering current is very small. The energy exchange between the scattering electrons and nuclear motion will result in an inelastic component in the transmission current. The nuclear motion will introduce vibrational excited states which are the ones that contribute to the inelastic component in the case of off-resonant excitation. If the transmission is far below unity, the inelastic component can lead to a second tunneling path, which gives an additional current contribution to the tunneling current. While in case of a close to unity transmission the inelastic current can reduce the current (have a negative sign) by producing a “dip” in the inelastic tunneling spectrum. According to the characteristics of structure, the four molecular junctions studied in this paper can be seen as two major categories. The first system is that by connecting the hydrogen atom passivated AC edges with Au electrodes to form molecular junctions, and the ZZ edges modified by pure hydrogen or donor–acceptor pairs as the main scattering molecular core region. The other system is that by connecting the pure hydrogen atom or donor–acceptor pairs modified ZZ edges with Au electrodes to form molecular junctions, and the AC edges passivated by pure hydrogen as the central scattering molecular core region. We know that the electrode connections mainly affect the contact conductance. As the central scattering region, the actual composition and structure of the central portion of the extended molecule is the main electron transport channel of the devices. The electronic structure and molecular orbital distribution characteristics directly determine the tunneling conductance through the devices. Thus, functional modification on the open edges or body atoms of finite-sized GNR slices has become an important means to control the overall distribution of the carrier and the transport properties of the devices. The calculated inelastic tunneling spectrums of the four junctions as a function of applied bias voltage at room temperature have been shown in Fig. 2.

Fig. 2. The inelastic electron tunneling spectroscopy as the function of source–drain bias voltage of the H–H AC, H–H ZZ, A–D AC, and A–D ZZ systems at room temperature a.u..

The main research point of this work is illustrating the effects of electrode connection types and central molecular modification on the inelastic tunneling current of the systems. So we have adopted arbitrary units in Fig. 2. The inelastic current is very small, only a few minus magnitude of 10. It is known that the comparisons of the direct intensity of IETS curves between different systems have little significance. The relative intensity of the peaks is important information. By comparing the IETS peaks, we conclude that the peak intensity and peak position of the four systems are quite different. The intensity of IETS partly reflects the strength of atomic vibrations. Thus, we may conclude that the ZZ systems are more stable than the AC systems. From Fig. 2 one can see that the inelastic tunneling spectrum is sensitive to the atom structure and component of the central molecular core. Based on the results of the four junction models, one can see that the main inelastic scattering appeared in the range from 0 V to 0.2 V, presenting as large peaks. There is a relatively small peak and a “dip” in the area 0.3 V~ 0.4 V as shown in Fig. 2. The introductions of donor–acceptor functional groups have a significant impact on the inelastic tunneling spectrum. Comparing with the results of the two pure hydrogen passivation systems H–H AC and H–H ZZ as shown in Figs. 2(a) and 2(b), one can see that the different electrode connection types and the edge termination structures of the central GNR slices have a certain influence on the IETS curves. There are some differences on the peak position and peak broadening. Comparing with the results of H–H AC and A–D AC systems shown in Figs. 2(a) and 2(c), we can see that the inelastic tunneling spectrum will have an overall slight shift to the low energy region and the inelastic contact conductance near the Fermi level also slightly increased by using donor–acceptor groups as the link group. Comparing with the results of H–H ZZ and A–D ZZ systems shown in Figs. 2(b) and 2(d), one can conclude that the inelastic current for the lower energy region increases obviously when using donor–acceptor functional groups as the edge modification types of the central scattering area. It needs to be mentioned that a new peak of the IETS curve appears near the Fermi level, and a number of small vibrational peaks and “dips” appear at higher energy regions. The reason may be that the introduction of donor–acceptor functional groups causes the rehybridization of edge carbon-groups, and the nuclear motion for the systems is much stronger than that of the pure carbon-hydrogen ones. The nuclear motion can introduce vibrational excited states which contribute to the inelastic electron scattering. The metal atoms considered in the extended molecules will also bring some low frequency vibration modes. Furthermore, the donor–acceptor groups will also have an effect on the carrier concentration and distribution of the molecular core, thus the electronic properties of the system and the transport properties of the junctions will be tuned. These two mechanisms can tune the molecular orbitals and thus change the transport properties of the devices.

3.2. The IETS of H–H ZZ and A–D ZZ systems at low temperature

It is known that the IETS is a powerful spectroscopic tool for molecular identification and chemical bonding investigations. In order to see the influence of the donor–acceptor groups on the IETS curves more clearly, in this part, we focused on two systems H–H ZZ and A–D ZZ and calculated the IETS at low temperature 4.2 K. The calculated results are shown in Fig. 3. From Fig. 3 one can see that the IETS curves show significant fine structure at low temperature. For the pure carbon-hydrogen system H–H ZZ, all of the peaks come from the vibration of carbon and hydrocarbon atoms or groups. The strongest peak appears at the energy region between 0.1 V~ 0.2 V. By introducing donor–acceptor pairs, there are two significant changes of the IETS. Firstly, comparing with the pure carbon-hydrogen system, new IETS peaks appear at multiple energy regions after the introduction of donor–acceptor groups. These peaks come from the vibration mode of atoms for the donor–acceptor groups and coupling between edge groups. Therefore, the IETS can be used as one of the qualitative detection methods of the composition of micro systems by comparing with the various vibrational modes obtained in experiments. Secondly, the intensity distributions as a function of the bias voltage of the IETS have been changed after the introduction of donor–acceptor groups. The peak with maximum intensity appears near the Fermi level, and the small peak near 0.4 V has split into two peaks. The redistribution of the IETS peak intensity illustrates that the carrier concentration and distribution of the system have been changed and tuned by introducing donor–acceptor groups. Thus, the functional modification becomes an important means to manipulate the electronic transport properties of molecular junction systems.

T=4.2 K.

'>		Fig. 3. The inelastic electron tunneling spectroscopy as the function of source–drain bias voltage of the H–H ZZ and A–D ZZ system under lower temperature T=4.2 K.
3.3. Temperature dependence of inelastic electron scattering

It is known that the electron scattering process is sensitive to temperature. Furthermore, temperature also has a certain impact on the molecular motion, thus we discuss the temperature dependence of the IETS in this part. All of the transport properties have been calculated by the QCME code. The theoretical calculation methods of QCME show that there are two main factors which have exponential dependence on temperature closely related to temperature: the population distribution of thermal particles, which can be calculated using the Boltzmann distribution function Pn and the electron Fermi distribution at the end of source and drain electrodes f(E), where

(2)
source:
and drain:

By using the A–D ZZ system as an example, we calculate the IETS under different working temperatures (from 4.2 K to 298 K). The results are shown in Figs. 4(a) to 4(f). From Fig. 4 one can see that the IETS curves show a significant fine structure at lower temperatures. With the increasing of temperature, each peak widened more and more obviously. Each peak broadening covers many fine structures of the IETS curve. When increasing to room temperature 298 K, there are only three characteristic peaks which are located in near 20 mV, 100 mV, and 210 mV on the IETS curve. From 35 K, the peaks of IETS have been significantly widened. The characteristics and change trend of the IETS curves are quite similar to that of higher temperatures. In the experiment, the preparation and characterization of materials and devices are more difficult to achieve at very low temperatures. This requires higher experimental conditions and higher cost. It is necessary to mention that the interaction between electron and molecular dipoles also plays a role in IETS at a high temperature. The IETS curves measured at much higher temperatures cannot be used to identify the atomic structures of the molecular devices. The results also show that there is a peak of IETS near 400 mV. The intensity of this peak is very small. The high-frequency vibration modes are mainly from the contribution of the molecules. The metal atoms considered in the extended molecules will bring some low frequency vibration modes. For the A–D ZZ system, by introducing the A–D pairs, new molecular vibrational levels which were derived from the metal atoms and metal-molecule vibration have been introduced. Thus, the changes of IETS in the low-frequency region are partially caused by the introduction of the donor–acceptor groups. The population distributions of thermal particles also have certain effects on the IETS in the lower-frequency region. Due to the fact that energy difference is often close to zero in the vicinity of the conducting orbits, the effect of Fermi distribution on the tunneling current is persistent.

Fig. 4. (a)–(f) The inelastic electron tunneling spectroscopy under different working temperatures for the A–D ZZ system.
4. Conclusions

In this paper, the inelastic tunneling spectroscopy of four junctions based on 8 × 8 finite-sized GNR slices have been calculated. Two edge functional modification types with hydrogen and donor–acceptor pairs have been considered. The IETS curves are sensitive to the atomic structures and electrode connection types of the systems. Comparing with the pure carbon-hydrogen systems, the donor–acceptor functional groups have effects on the rehybridization of edge carbon-groups and the carrier concentration and distribution of the molecular core. The nuclear motion and coupling between the electrodes and molecular core will introduce vibrational excited states which contribute to the inelastic electron scattering. New IETS peaks appear at multiple energy regions and the intensity distributions as a function of bias voltage of the IETS have been changed after the introduction of donor–acceptor groups. These changes mainly come from the vibration mode of atoms for the donor–acceptor groups and coupling between edge groups. Therefore, the IETS curves can be used as one of the qualitative detection methods of the composition of micro systems by comparing with the various vibrational modes obtained in experiments. For the temperature dependence of IETS, results show that the changes of IETS in the low-frequency region are caused by the introduction of the donor–acceptor groups and the population distribution of thermal particles, and that the effect of Fermi distribution on the IETS is persistent.

Reference
[1] Liu J Q Tang J G Justin Gooding J 2012 J. Mater. Chem. 22 12435
[2] Sun P Z Zhu M Wang K L Zhong M Wei J Q Wu D H Zhu H W 2013 ACS Appl. Mater. Interfaces 5 9563
[3] Wang X W Sun G Z Routh P Kim D H Huang W Chen P 2014 Chem. Soc. Rev. 43 7067
[4] Segawa Y Ito H Itami K 2016 Nat. Rev. 1 1
[5] Zhang L Wang J 2014 Chin. Phys. B 23 087202
[6] Zhang L 2015 Chin. Phys. B 24 117202
[7] Cobas E Friedman A L Erve O M Jvan’t Robinson J T Jonker B T 2012 Nano Lett. 12 3000
[8] Bao Q L Loh K P 2012 ACS Nano 6 3677
[9] Zhang H L Sun L Wang D 2016 Acta Phys. Sin. 65 016101 in Chinese
[10] Wang X L Shi G Q 2015 Energy Environ. Sci. 8 790
[11] Pan L J Zhang J Chen W G Tang Y N 2015 Chin. Phys. Lett. 32 36101
[12] Yang Y E Xiao Y Yan X H Dai C J 2015 Chin. Phys. B 24 117204
[13] Yoon T Kim J H Choi J H Jung D Y Park I J Choi S Y Cho N S Lee J I Kwon Y D Cho S Kim T S 2016 ACS Nano 10 1539
[14] Song H Reed M A Lee T 2011 Adv. Mater. 23 1583
[15] Zhu J H Chen M J He Q L Shao L Wei S Y Guo Z H 2013 RSC Adv. 3 22790
[16] Qi Z J Rodríguez-Manzo J A Botello-Méndez A R Hong S J Stach E A Park YW Charlier J C Drndić M Johnson A T C 2014 Nano Lett. 14 4238
[17] Mali K S Greenwood J Adisoejoso J Phillipson R Feyter S De 2015 Nanoscale 7 1566
[18] Li C X Deng X Q Sun L 2016 Acta Phys. Sin. 65 068503 in Chinese
[19] Ding Z L Jiang J Xing H Z Shu H B Huang Y Chen X S Lu W 2011 J. Comput. Chem. 32 1753
[20] Wang W Y Lee T Reed M A 2004 J. Phys. Chem. B 108 18398
[21] Chen Y C Zwolak M Di Ventra M 2005 Nano Lett. 5 621
[22] Troisi A Ratner M A 2007 Phys. Chem. Chem. Phys. 9 2421
[23] Kim Y S Hellmuth T J Burkle M Pauly F Scheer E 2011 ACS Nano 5 4104
[24] Long D P Troisi A 2007 J. Am. Chem. Soc. 129 15303
[25] Cao H Jiang J Ma J Luo Y 2008 J. Phys. Chem. C 112 11018
[26] Shizu K Sato T Tanaka K 2010 Nanoscale 2 2186
[27] Fock J Sørensen J K Lörtscher E Vosch T Martin C A Riel H Kilså K Bjørnholma T van der Zant H 2011 Phys. Chem. Chem. Phys. 13 14325
[28] Wegner D Yamachika R Zhang X W Wang Y Y Crommie M F Lorente N 2013 Nano Lett. 13 2346
[29] Ortmann F Radke K S Günther A Kasemann D Leo K Cuniberti G 2015 Adv. Funct. Mater. 25 1933
[30] Maccariello D Taleb A A Calleja F de Parga A L V Perna P Camarero J Gnecco E Farías D Miranda R 2016 Nano Lett. 16 2
[31] Becke A D 1993 J. Chem. Phys. 98 5648
[32] Lee C Yang W Parr R G 1988 Phys. Rev. B 37 785
[33] Jiang J Wang C K Yi L Quantum chemistry for molecular electronic QCME-V1.1 (Software)
[34] Wang C K Luo Y 2003 J. Chem. Phys. 119 4923
[35] Jiang J Kula M Luo Y 2006 J. Chem. Phys. 124 034708
[36] Troisi A Ratner M A Nitzan A 2003 J. Chem. Phys. 118 6072