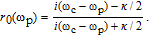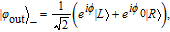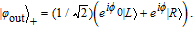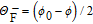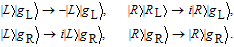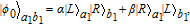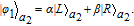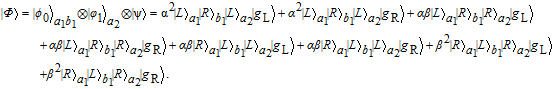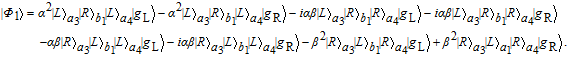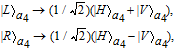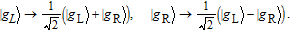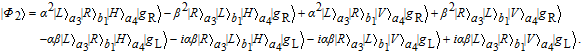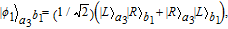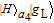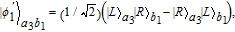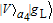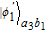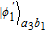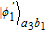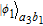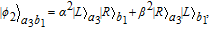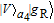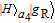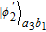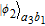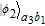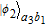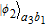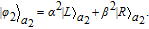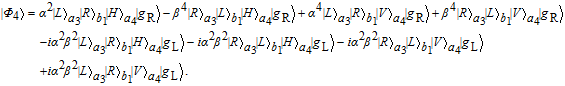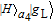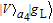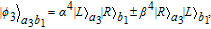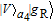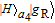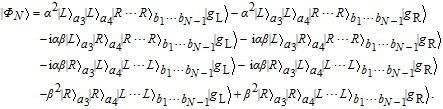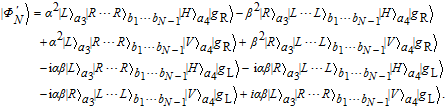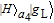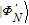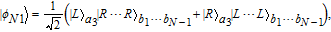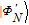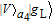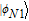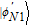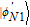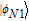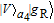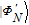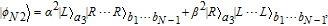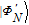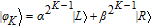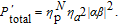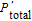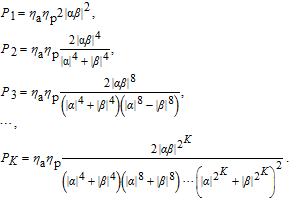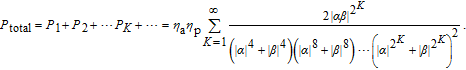Optimal multi-photon entanglement concentration with the photonic Faraday rotation
1. IntroductionIn the last few decades, quantum information technology has developed with extremely high speed. Both theory and experimental results demonstrate that the quantum communication and computation are much more efficient than their classical counterparts in many aspects. Entanglement is an extremely important resource in almost all the practical quantum communication and computation tasks, such as quantum cryptography,[1] quantum teleportation,[2,3] quantum dense coding,[4] quantum secure direct communication,[5–9] quantum repeaters,[10,11] entanglement-based quantum key distribution,[12,13] and some other quantum communication fields.[14–18] During the past decade, research groups have successfully generated many different single-particle and multi-particle entanglement states.[19–24] Among the large number of entanglement states, the maximally entangled state is one of the most important entanglement states, which is often adopted to construct the quantum entanglement channel in almost all quantum communication tasks. However, as the entangled particles interact with the channel noise during the storage and transmission process, the decoherence is inevitable. The decoherence can make the maximally entangled state degrade to the mixed state or pure less-entangled state, which cannot be used to set up the high quality quantum entanglement channel. Even worse, they may make the quantum communication insecure.[25] Therefore, both the two kinds of decoherence states should be recovered into the maximally entangled states prior to the practical application.
Entanglement concentration is an efficient method for distilling the maximally entangled quantum states from pure less-entangled states.[26–63] The concept of entanglement concentration protocol (ECP) was proposed by Bennett et al. in 1996, which is called the Schmidt projection method.[26] In the entanglement concentration protocol, some collective and nondestructive measurements are required, which cannot be realized under current experimental conditions. After that, various research groups proposed many efficient entanglement concentration protocols in the optic and solid systems, successively. For example, in 1999, the entanglement concentration protocol based on entanglement swapping was proposed by the Bose group.[27] Soon after, Shi et al. put forward an improved entanglement concentration protocol.[28] In 2001, Zhao et al. and Yamamoto et al. independently proposed two similar entanglement concentration protocols,[29,30] in which they first adopt the optical polarization beam splitters (PBSs) to complete the parity check measurement for the photons. In 2008, Sheng et al. constructed the quantum non-demolition detector with the help of the cross-Kerr nonlinearity. With the quantum nondemolition detector, they proposed a recyclable entanglement concentration protocol, which can increase the success probability largely.[31] In 2012, Sheng et al. proposed two entanglement concentration protocols assisted with a single photon, which can largely economize the entanglement resource.[32,33] So far, most entanglement concentration protocols cannot deal with the multi-particle entanglement, for its high operational complexity. Only a few entanglement concentration protocols can deal with the decoherence problem in the multi-photon system.[50–60]
The cavity is a highly-efficient platform for performing the quantum information tasks, because the interaction between atoms and photons in the cavity can be well controlled.[64–78] In the quantum information tasks, we can adopt the spatially separated cavities to be quantum nodes by making the atoms strongly interact with the local cavities. They can also construct a quantum network with the help of the photons, which act as quantum buses.[70,74–76] In 2008, the input-output process relevant to optical low-quality (Q) cavities has been achieved.[79] In 2009, the group of An obtained a general expression for the input-output process of the photon-atom system in the low-Q cavity, which can cause a certain angle rotation of the photonic polarization, that is, the photonic Faraday rotation.[80] In 2012, with the help of the photonic Faraday rotation effect, Peng et al. proposed an entanglement concentration protocol for the multi-photon Greenberger–Horne–Zeilinger (GHZ) state.[81] This entanglement concentration protocol is not optimal, for they need to consume two pairs of pure less-entangled multi-photon GHZ states to distill one pair of maximally entangled GHZ states with some probability, and the other one pair of less-entangled multi-photon GHZ states is wasted. In this paper, we put forward an optical entanglement concentration protocol for distilling the maximally entangled photonic GHZ state from one pair of less-entangled photonic GHZ states and an auxiliary single photon based on the photonic Faraday rotation. Our entanglement concentration protocol is an improvement of the entanglement concentration protocol in Ref. [81], for it can save a pair of less-entangled GHZ states and reach the same success probability of Ref. [81]. Moreover, our entanglement concentration protocol is recyclable. By repeating the entanglement concentration protocol, the discarded items of Ref. [81] can also be concentrated, which can largely increase the success probability. Especially, under practical imperfect experimental conditions, our entanglement concentration protocol shows greater application potential than the entanglement concentration protocol proposed in Ref. [81].
The paper is organized as follows. In Section 2, we introduce the photonic Faraday rotation in low-Q cavity. In Section 3, we explain the entanglement concentration for the two-photon state. In Section 4, we introduce the entanglement concentration for the multi-photon GHZ state. In Section 5, we provide a discussion and conclusion.
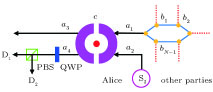
2. Basic theoretical model of the photonic Faraday rotationWe briefly explain the basic principle of the photonic Faraday rotation. Suppose a three-level atom is trapped in the low-Q cavity. As shown in Fig. 1,[82–85] |g
L〉 and |g
R〉 are two degenerate ground states and |e〉 is an excited state. Suppose a single photon pulse |φin〉 = (1/√2)(|L〉+|R〉) (|L〉: left-circularly polarization, |R〉: right-circularly polarization) enters the low-Q cavity and interacts coherently with the atom. During the interaction process, the atom will achieve the transition |g
L〉↔|e〉 (|g
R〉↔|e〉) by absorbing or emitting a photon in |L〉 (|R〉), respectively. As shown in Refs. [80] and [86]–[88], the general expression of the reflection coefficient of the atom–cavity system can be written as
In Eq. (1), κ and γ are the cavity damping rate and atomic decay rate, respectively. ω
p, ω
c, and ω
0 are the frequency of the input photon, the cavity, and the atom, respectively. g is the atom–cavity coupling strength. Equation (1) can be rewritten as a pure phase shift r(ω
p) ≈ eiϕ
. If the atom uncouples to the cavity, which makes g = 0, we can simplify Eq. (1) to
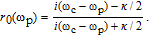 | (2) |
Equation (
2) can be rewritten as
r
0(
ω
p) =
e
iϕ
0
.
Therefore, under the atom state of |g
L〉, the photon state will evolve to
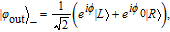 | (3) |
while under the atom state of |
g
R〉, the photon state will evolve to
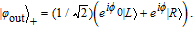 | (4) |
It can be found that the polarization direction of the output photon rotates an angle
or
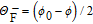
, which is the so-called photonic Faraday rotation.
According to Eqs. (1) and (2), it can be seen that under the special condition that ω
0 = ω
c, ω
p = ω
c-κ/2, γ = 0, if g = κ/2, we can obtain r(ω
p) = −1 (ϕ = π), while if g = 0, we can obtain r
0(ω
p) = i(ϕ
0 = π/2). In this way, the output photon–atom state will evolve to[81]
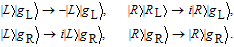 | (5) |
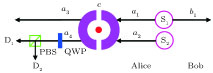
3. Efficient concentration for two-photon stateHere, we first explain the concentration for the two-photon state, which is the simplest case. The basic theoretical model is shown in Fig. 2. Alice and Bob share a less-entangled two-photon state generated from the entanglement source S1 with the form of
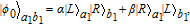 | (6) |
where
α and
β are initial entanglement coefficients, and |
α|
2+|
β|
2 = 1.
For realizing the entanglement concentration, Alice makes the single photon source S2 generate an auxiliary single photon as
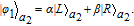 | (7) |
Meanwhile, she makes a three-level atom with the following form: |
ψ〉 = (1/√2)(|
g
L〉 + |
g
R〉) encode in a low-
Q cavity
c. Therefore, the whole photon-atom system can be written as
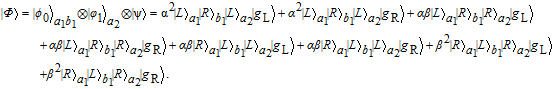 | (8) |
Next, Alice makes the photons in a1 and a2 modes enter the low-Q cavity c to interact with the three-level atom, successively. Based on the input–output relation rule in Eq. (5), |φ〉 can evolve to
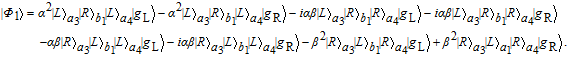 | (9) |
After the photons exit the cavity, Alice performs a Hadamard (H) operation on the photon in a4 mode and the three-level atom. The H operation on the auxiliary photon can be easily performed by making the photon pass through a quarter-wave plate (QWP), which makes
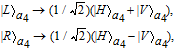 | (10) |
where |
H〉 and |
V〉 represent the horizontal and vertical polarization, respectively. The
H operation on the atom can be performed by driving it with an external classical field (polarized lasers), which will lead to
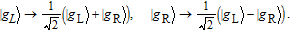 | (11) |
After the
H operations, the state in Eq. (
9) can ultimately evolve to the following equation
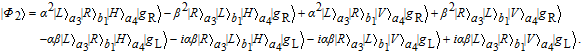 | (12) |
Then, Alice makes the photon in a4 mode enter the polarization beam splitter (PBS), which can transmit the photon in |H〉 and reflect the photon in |V〉, respectively. Finally, she measures the photons in the two output modes by the detectors D1 and D2, and the three-level atom. Based on her measurement results, |φ
2〉 in Eq. (12) may collapse to four possible cases. For example, |φ
2〉 will collapse to
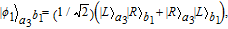 | (13) |
when the measurement result is
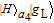
, while |
φ
2〉 will collapse to
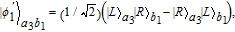 | (14) |
when the measurement result is
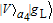
. Both
and
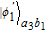
are the maximally entangled two-photon states. If
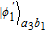
is obtained, Alice can transform
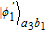
to
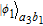
by performing the phase-flip operation. Until now, our concentration process is completed, and we recover the less-entangled two-photon state into the maximally entangled state. The success probability is
P
1 = 2|
αβ|
2, which equals to that of the ECP in Ref. [
81].
On the other hand, |φ
2〉 in Eq. (12) will collapse to
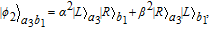 | (15) |
when the measurement result is
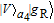
, equation (
12) will collapse to
 | (16) |
when the measurement result is
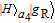
. With the help of the phase-flip operation, Alice can also convert
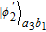
to
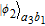
. Interestingly, it can be found that
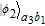
has the similar form with |
ϕ
0〉 in Eq. (
6). In this way,
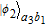
is a new less-entangled two-photon state. According to the concentration step described above, Alice can reconcentrate
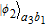
for the next concentration round.
In the second concentration round, S2 generates another auxiliary single photon in a
2 mode with the form
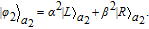 | (17) |
Alice makes the two photons in her location interact with the three-level atom in the low-
Q cavity, successively. Similarly, based on Eq. (
5), the whole photon–atom state can evolve to
 | (18) |
After the
H operation, |
φ
3〉 can evolve to
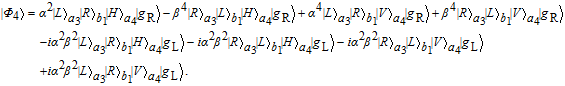 | (19) |
Finally, by measuring the output auxiliary photons and the three-level atom, |φ
4〉 in Eq. (19) can also collapse to four possible cases. It will collapse to
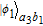or
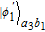, corresponding to the measurement result of
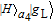or
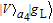respectively. Therefore, we can obtain the maximally entangled two-photon state in the second concentration round, with the success probability of
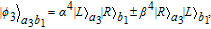 | (20) |
where ‘+’ corresponds to
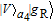
and ‘−’ corresponds to
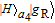
. Both of them can be reconcentrated for the third round.
In this way, it can be found that by providing an auxiliary photon with the form
 | (21) |
Similar to in Section 3, the single photon source S2 generates an auxiliary photon with the form of Eq. (7) in a
2 mode. Alice makes the photons in a
1 and a
2 modes pass through the low-Q cavity c and interact with the three-level atom, successively. After the cavity, the whole photon–atom state will evolve to the following expression
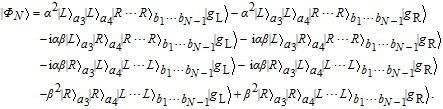 | (22) |
Then, Alice needs to perform the H operation on the photon in a
4 mode and the atom. After that, |φ
N〉 in Eq. (22) will ultimately evolve to
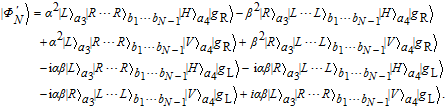 | (23) |
Finally, the states of the auxiliary single photon and the atom are measured by Alice. If she obtains
,
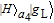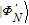will collapse to
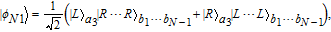 | (24) |
while
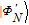
will collapse to
 | (25) |
corresponding to the measurement result of
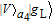
. Both
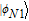
and
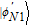
are maximally entangled
N-photon GHZ states. Alice can also convert
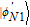
to
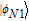
with the help of the phase-flip operation. Therefore, we have successfully recovered the less-entangled
N-photon GHZ state into the maximally entangled state. The success probability is still
P
1N
= 2|
αβ|
2, which is the same as the success probability
P
1 in Section
3.
On the other hand, if Alice obtains the measurement result of
,
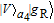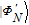in Eq. (23) will collapse to
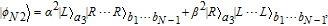 | (26) |
while if she obtains
,
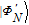
will collapse to
 | (27) |
which can also be converted to |
ϕ
N2〉. It is obvious that |
ϕ
N2〉 is a new less-entangled
N-photon GHZ state, which can be reconcentrated for the next round. In this way, Alice only needs to provide a suitable auxiliary single photon with the form
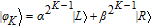
in the
K-th concentration round; she can repeat the ECP to distill the maximally entangled GHZ state from the discarded items. The success probability in each concentration round is totally the same as that for the concentration of the two-photon state.
5. Discussion and summaryIn our ECP, based on the photonic Faraday rotation in the low-Q cavity, we can probabilistically recover the less-entangled multi-photon GHZ state into the maximally entangled state. Our ECP is an improvement for the ECP in Ref. [81] for the following reasons. First, the ECP in Ref. [81] needs to consume two pairs of less-entangled multi-photon GHZ states to distill one pair of maximally entangled states, while our ECP only requires one pair of less-entangled multi-photon GHZ states and an auxiliary photon. It makes our ECP much more economical. Second, in Ref. [81], after performing the ECP, all the N parties should measure the photon states. Then, they can judge whether they obtain the maximally entangled GHZ state by checking all the measurement results of the N parties. It greatly increases the operational complexity, especially under the case of large photon number N. Our ECP only requires local operations by Alice, and she can judge whether the concentration is successful only by her own measurement results. Under the successful concentration case, she tells the other N−1 parties to preserve their photons. In this way, it can simplify the operation largely. Third, if the concentration fails, Alice can repeat it to concentrate discarded items in Ref. [81]. It makes the success probability of our ECP much higher than the ECP in Ref. [81].
In the concentration process, both the atom and photon detections play key roles. Under current experimental conditions, both detections are imperfect: their detection efficiencies are lower than 100%. Therefore, it is necessary to consider the influence of the detection efficiency on the success probability. Here, we suppose that η
p and η
a are the single photon detection efficiency and the single atom detection efficiency, respectively. In the ECP of Ref. [81], as the parties should measure a pair of N-photon states and the single atom state, its success probability can be written as
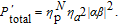 | (28) |
It is obvious that
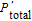
is exponentially reduced with the growth of the photon number
N. Fortunately, in each concentration round of our ECP, only the auxiliary single photon and the single atom should be measured. According to the description of Section
3 and Section
4, the success probability in each concentration round can be calculated as
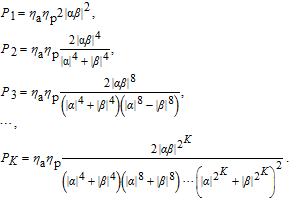 | (29) |
The total success probability (
P
total) of our ECP equals to the sum of the success probability in each concentration round. Therefore, we can calculate it as follows:
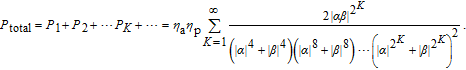 | (30) |
It can be found that the photon number
N does not influence the
P
total.
Recently, Heine et al. reported their research result on the single atom detection. They have achieved η
a = 66% in the experiment.[89] Moreover, they have shown that with some improvement, the single atom detection efficiency can achieve η
a > 95% in theory. The single photon detection has been a big difficulty under current experimental conditions, for the quantum decoherence effect of the photon detector.[90] In the optical range, η
p is usually less than 30%.[90,91] Lita et al. reported their experimental result about the near-infrared single-photon detection. They showed the η
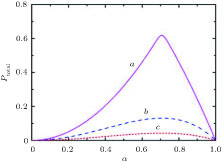
p at 1556 nm can reach 95± 2%.[92] Based on their research results, we make the numerical simulation on the total success probability (P
total) of both ECPs. Figure 4 shows the P
total varying with the entanglement coefficient α.
In Fig. 4, we assume η
p = η
a = 80%. In curve a, we repeat our ECP 5 times, while in curve b and curve c, the photon number for the ECP in Ref. [81] is controlled to be N = 5 and N = 10, respectively. It is obvious that P
total of the ECP in Ref. [81] reduces largely with the growth of N. When N is large, the
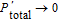. On the other hand, as shown in curve a, by repeating our ECP, the P
total can be largely increased. Meanwhile, as the P
total of our ECP is not influenced by the photon number N, it can still keep a high value in the practical application with a large value of N.
In summary, we proposed an optimal ECP to distill the maximally entangled multi-photon GHZ state from an arbitrary less-entangled GHZ state based on the input–output relations in the low-Q cavity. Our ECP is an improvement on the ECP in Ref. [81]. On one hand, the ECP in Ref. [81] requires two copies of less-entangled multi-photon GHZ states to be consumed, while our ECP only requires one copy of a less-entangled multi-photon GHZ state and an auxiliary photon. It makes our ECP much more economical. On the other hand, the ECP in Ref. [81] relies on the nonlocal operations from N parties, while our ECP only requires the local operation from Alice. In this way, the experimental operation of our ECP is much easier. Moreover, the distilled photon state can be well preserved and we can repeat the ECP to reuse the discarded items in the ECP of Ref. [81] by repeating our ECP. It makes the success probability of our ECP much higher than that of the ECP in Ref. [81]. Under practical imperfect detection conditions, the success probability of the ECP in Ref. [81] is exponentially reduced with the photon number N, while in our ECP, a relatively high success probability can still be obtained, which is not influenced by N. Based on all the features mentioned above, our ECP has a good application potential in current and future quantum communications.
