Cite this Article
Hu Ji-Ying, Li Zhao-Hui, Sun Yang, Li Qi-Hu. Investigations of thickness-shear mode elastic constant and damping of shunted piezoelectric materials with a coupling resonator. Chinese Physics B, 2016, 25(12): 127701  
Permissions
Investigations of thickness-shear mode elastic constant and damping of shunted piezoelectric materials with a coupling resonator
Hu Ji-Ying1, Li Zhao-Hui1, †, , Sun Yang1, 3, Li Qi-Hu2
Department of Electronics, Peking University, Beijing 100871, China
Advanced Technology Institute, Peking University, Beijing 100871, China
College of Science, Beijing Forestry University, Beijing 100083, China

 

† Corresponding author. E-mail: lizhcat@pku.edu.cn

Project supported by the National Defense Foundation of China (Grant No. 9149A12050414JW02180).

Abstract
Abstract

Shear-mode piezoelectric materials have been widely used to shunt the damping of vibrations where utilizing surface or interface shear stresses. The thick-shear mode (TSM) elastic constant and the mechanical loss factor can change correspondingly when piezoelectric materials are shunted to different electrical circuits. This phenomenon makes it possible to control the performance of a shear-mode piezoelectric damping system through designing the shunt circuit. However, due to the difficulties in directly measuring the TSM elastic constant and the mechanical loss factor of piezoelectric materials, the relationships between those parameters and the shunt circuits have rarely been investigated. In this paper, a coupling TSM electro–mechanical resonant system is proposed to indirectly measure the variations of the TSM elastic constant and the mechanical loss factor of piezoelectric materials. The main idea is to transform the variations of the TSM elastic constant and the mechanical loss factor into the changes of the easily observed resonant frequency and electrical quality factor of the coupling electro–mechanical resonator. Based on this model, the formular relationships are set up theoretically with Mason equivalent circuit method and they are validated with finite element (FE) analyses. Finally, a prototype of the coupling electro–mechanical resonator is fabricated with two shear-mode PZT5A plates to investigate the TSM elastic constants and the mechanical loss factors of different circuit-shunted cases of the piezoelectric plate. Both the resonant frequency shifts and the bandwidth changes observed in experiments are in good consistence with the theoretical and FE analyses under the same shunt conditions. The proposed coupling resonator and the obtained relationships are validated with but not limited to PZT5A.

PACS: 77.90. + k;62.20.−x;62.20.de;81.40.Jj
Keyword:piezoelectric materials;shunt damping;shear mode;elastic constant
1. Introduction

The piezoelectric shunt damping technology has been the focus of many research fields, especially in the fields of vibration control,[1–7] sound absorption,[8–11] and noise elimination,[12,13] wave propagation control,[14] where the shunt damping is usually realized with a shunted piezoelectric patch working in one of three modes:[2] the transverse mode, the longitudinal mode, and the shear mode.

As the shear mode has the advantage over the other two modes by using the surface or interface stresses, it has increasingly attracted extensive research interests in surface vibration suppression with shunt-damping technologies.[15–20] For example, Benjeddou and Ranger investigated the use of shear-mode piezoelectric ceramics for shunted passive vibration damping and found that the added resistive shear-mode shunt damping is twelve times more than the classical resistive extension-mode shunt damping.[16] Karim Blanzé designed a bolted joint for reducing the vibration of a structure by taking advantage of the shear mode to utilize the surface or interface stress.[18] dos Santos and Trindade studied active–passive piezoelectric networks (APPN) for extension and shear modes, and they find that the shunt-damping effect of the shear mode is better than that of the extension mode.[19]

Among these applications, the thick-shear mode (TSM) elastic constant c55 and the mechanical loss factor are the most essential parameters that determine the performance of the vibration damping system by utilizing the shear mode of piezoelectric materials. Therefore, it is of great research value to investigate the relationships between the TSM elastic constant c55 as well as the mechanical loss factor and different shunt circuits, which are essential to the design or control of a shunt-damping system by using the shear mode of piezoelectric material.

In practice, the direct measurements of the shear moduli of elastic or viscoelastic materials are of great complexity and difficulty.[21] Thus, indirect methods utilizing the velocity of sound,[22] the relationship between the resonant and the anti-resonant frequencies of a regular-cut shear mode plate are usually employed to estimate the shear moduli of piezoelectric materials.[23] Some TSM piezoelectric or quartz crystal resonators have also been developed to implement their quantitative determinations of the shear moduli of polymers.[24–28] The resonator usually consists of a TSM piezoelectric or quartz crystal layer and one- or multiple-layer polymer films, of which the basic principle is that shear modulus and damping of polymer film can change the resonant frequency and bandwidth of a TSM piezoelectric resonator obtained through an impedance analyzer, where the resonant frequency shift reflects the shear modulus and the bandwidth change reflects the mechanical loss factor of the tested material.

However, the above mentioned methods[22–28] cannot be used to investigate the variations of the TSM elastic constant c55 and the mechanical loss factor of a piezoelectric material with different shunt circuits. The viable testing system should satisfy the following requirements. First, the piezoelectric material that is shunted to circuits should not be used for impedance measurement, because the direct electrical coupling will cover the mechanical parameter effect on the impedance. There should be another piezoelectric material serving as the tested one which is electrically isolated from the shunted one, so that the impedance of the tested one can reflect the mechanical parameter change of the system, rather than the coupling electrical impedance. Second, if a two-plate piezoelectric resonator is adopted, two piezoelectric plates should work at a pseudo electrostatic state to avoid the mutual influence of their natural resonant frequencies. Thus the system should be resonant at a frequency far below the natural frequencies of the piezoelectric plates, which meanwhile provides a nearly linear relationship between the resonant frequency shift of the resonator and the modulus change.

In our previous work, we have proposed an indirect method to investigate the influence of shunt circuits on elastic constant c33 and the mechanical loss factor of thickness mode.[29] Inspired by this idea, in this paper we propose a coupling TSM electro–mechanical resonator to investigate the variations of the elastic constant c55 and the mechanical loss factor of the shear-mode piezoelectric materials shunted to different circuits. The proposed TSM resonator consists of two identical shear-mode piezoelectric plates and a mass block to form a coupling resonant system. One of the two plates is employed to change its TSM elastic constant and mechanical loss factor by connecting in parallel different shunt circuits, while the other is used to test the electrical admittance-frequency curve of the system. The measurement circuit and the shunting circuit are electrically separated to avoid the mutual interference. The mass is employed to lower the first resonant frequency of the system significantly to provide a pseudo electrostatic state. Mason equivalent circuit method is adopted to make the theoretical analyses and the finite element method (FEM) is employed to conduct the simulations. A prototype of the resonator model is fabricated to verify the theoretical analyses and simulations, with which the variations of the TSM elastic constant c55 and the mechanical loss factor of the PZT5A plate shunted to different circuits are investigated.

2. Model description

An electro–mechanical resonant system, i.e., a resonator, is proposed to measure the change of the resonant frequency of the system with shunt circuits, which is composed of two identical shear-mode piezoelectric ceramic plates a and b and a mass block m. They are bonded together tightly with a very thin layer of epoxy resin adhesive as shown in Fig. 1(a), where 1, 2, 3, and 4 are employed to mark the four surfaces or interfaces of a, b, and m respectively. Both surfaces 1 and 4 are set free to make force release boundary conditions. The mass block m is employed to make the resonant base frequency of the system much lower than the resonant frequency of a single piezoelectric plate itself to provide a quasi-static state.[4] The material of the mass block is of pure tungsten due to its high density to make the mass block close to a lumped-parameter element and the system close to an ideal spring oscillator. PZT-5A is chosen as the material of piezoelectric plates a, b in this paper, of which both are poled along the length direction (motion direction) and two electrodes are drawn from two faces of the thickness direction.

Fig. 1. Proposed coupling electro–mechanical resonant system: (a) the structure of the resonator; (b) equivalent coupling spring-mass system; (c) mechanical circuit diagram.

When plate b connects to different shunt circuits, i.e., Zx, its elastic constant c55 and the mechanical loss factor will change. Correspondingly, the resonant frequency and quality factor of the system will change too. By testing the electrical impedance of the resonator through plate a, the changes of the resonant frequency and quality factor of the system are obtained. Then the variations of c55 and the mechanical loss factor can be indirectly achieved. The separate circuits of two plates ensure the isolation of electrical effects of the shunted plate b on the tested plate a.

As shown in Fig. 1(b), the proposed system can be approximated as an equivalent ideal coupling spring-mass oscillator system, based on the lumped-parameter condition. It consists of three mass elements and two spring elements which are connected in series. The springs ka and kb are equivalent to the elastic constants of the two piezoelectric ceramic plates a and b respectively, and the mass elements Ma, Mb, and Mm correspond to the mass of the piezoelectric ceramic plates a and b and the mass block m respectively. The equivalent mechanical circuit diagram of the ideal spring oscillator system is given in Fig. 1(c), viewing from the bottom of plate a. Since the ceramic plate a is in open-circuit state, its elastic constant c55 keeps constant, i.e., the open-circuit elastic constant . Whereas the ceramic plate b is under different electrical boundary conditions, i.e., shunted to Zx, its elastic constant c55 is a variable.

In Fig. 1(c), ka and kb can be approximated as

Then the mechanical admittance Ym from the bottom of plates a can be derived as

From Eq. (3), it is found that the oscillator system has two resonant frequencies:

Here, fr2 is the natural resonant frequency of single ceramic plate, which does not change with kb, and fr1 is the resonant base frequency determined by the mass of block m and the variable kb, which is much lower than fr2, and is what we are concerned with in the research.

Hence, the stiffness of spring b can be obtained from

and the following relationship can be derived:

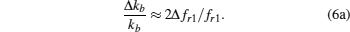
According to Eq. (1b), it has

or

Therefore, the variation of the elastic constant Δc55 can be obtained indirectly with the change of the resonant frequency Δfr1 of the resonator when plate b is shunted to different circuits. In fact, the relationship between c55 and the resonant frequency fr1 can also be determined if one value of the elastic constant c55 is provided at the resonant base frequency fr1.

3. Theoretical analysis with Mason equivalent circuit method

Because the two ceramic wafers a, b and the mass block m are tightly bonded together, the Mason equivalent circuit method[30] of the whole model can be obtained by connecting their respective equivalent circuit at mechanical terminals, which is shown in Fig. 2. Since surface 1 and surface 4 are free, the pressures on them are equal to zero and the two ends are short-circuited.

In Fig. 2,

where the subscripts ‘p’ and ‘m’ represent the piezoelectric ceramics and the mass block respectively. Correspondingly, ρp and ρm are their densities, Sp and Sm are their areas, and tp and tm are their thickness. Besides, and are the transverse wave velocities of piezoelectric ceramics in open state and shunted to circuits respectively, and and kp = ω/cp are the corresponding wave numbers, cm and km = ω/cm are the transverse velocity and wave number of the mass block m respectively. Both for the ceramic wafers a and b, is the inherent capacitance and is the electromechanical conversion factor, where is the dielectric constant and h15 is the shear-mode piezoelectric constant.

From Fig. 2, the electrical admittance Ya of the system calculated from the two electrodes of wafer a can be derived as

where “∥” means parallel connection, c55 are included in Zp1b and Zp2b through Eq. (7a) and cp.

Fig. 2. Electro–mechanical equivalent circuits of the whole model.

Equation (8) establishes an analytic relationship between electrical admittance Ya and shunted electrical impedance Zx. It is seen that when the piezoelectric ceramic plate b is open-circuited, i.e., Zx = ∞, the resonant frequency of the electrical admittance Ya is determined only by the static mechanical constants of plates a and b, and mass block m. However, if the piezoelectric ceramic plate b is shunted to an electrical impedance Zx, its TSM elastic constant c55 will change. As a result, reflecting in the electrical admittance Ya, the resonant base frequency will shift correspondingly.

From Eq. (8), an analytic relationship can also be established between the electrical loss factor ηe = 1/Qe of the system and the mechanical loss factor ηm = 1/Qm of the plate b. Here Qe is the electrical quality factor of the resonant peak and Qm is the mechanical quality factor of the plate b. The electrical quality factor Qe of the resonant peak can be solved through Eq. (8) by the inverse ratio of the relative bandwidth of the resonant peak as:

where fr is the resonant base frequency, f1 and f2 are two half-power frequencies around fr, which can be solved through Eq. (8) with . Here Ga is the real part of Ya, i.e., the conductance of the system. Since the piezoelectric ceramics have inner mechanical losses, the TSM elastic constant c55 of the plate b in Eq. (8) can be substituted with a complex number c55 = c55r + jc55i, where the subscripts ‘r’ and ‘i’ represent the real part and the imaginary part respectively. The imaginary part of the elastic constant reflects the mechanical loss. Defining the mechanical loss factor ηm as the ratio of the imaginary part to the real part of the elastic constant of the piezoelectric ceramics, it has

In view of Eqs. (8)–(10) and the definition of each variable, the analytic relationship between electrical loss factor ηe of the resonant peak and the mechanical loss factor ηm can be solved, which is not presented in the paper for simplicity due to its huge expression.

3.1. Properties of electrical conductance curve

Here, the electrical conductance of the system through plate a is calculated numerically to illustrate its properties. The precondition of using equivalent circuit method is that the length and width of the ceramic plates are both much larger than their thickness to meet the infinite boundary condition. Thus in the calculations, the dimension parameters are set to be l = w = 1000 mm, tp = 2 mm, and tm = 3 mm. As a matter of fact, since the shear mode is less affected by the lateral boundary condition than the thickness mode, if the length-to-thickness ratio is not too small, the lateral boundary effect on the resonant frequency of the system is negligible.

The material parameters of the piezoelectric ceramics (PZT-5A) and the mass block are listed in Table 1.

The elastic constant c55 of the ceramic wafer b is assumed to be a variable in the calculation to investigate the relationship between c55 and resonant frequency.

For c55 with a certain value, according to Eq. (8), the conductance (the real part of the admittance Ya) of the system measured from the two electrodes of wafer a can be calculated, then the resonant frequency and the electrical quality factor Qe can be obtained. For example, when the ceramic wafer b is in an open-circuit state, namely Zx = ∞ and , the conductance is calculated with the mechanical quality factor . As shown in Fig. 3, the conductance of the system shows a resonant peak at the frequency , which is the resonant base frequency of the system. The peak conductance can be extracted as Gamax = 57.58 S. By using two frequencies f1 = 146.6 kHz and f2 = 148 kHz, where the conductance is equal to , the electrical quality factor of the conductance is calculated as the following . Then the electrical loss factor of the system near the resonant peak is obtained, which is

Table 1.

Parameters of piezoelectric ceramics, mass block, and epoxy resin.

.
Fig. 3. Electrical resonant peak of the conductance of the system calculated from the two electrodes of the plate a (with wafer b in open-circuit, ).
3.2. Relationships drawn from the electrical conductance curve

Taking c55r as the unique variable with the other parameters of the model being constant, the relationship between and is calculated based on Eq. (8) as shown in Fig. 4(a). It can be observed that shows a linear variation with approximately in a wide range, which is in consistence with the conclusion in Eq. (6b). Therefore, if the variation of the resonant frequency is observed, the variation of the elastic constant real part c55r can be obtained.

Fig. 4. Relationships between (a) and , and (b) between ηm and ηe.

Similarly, taking the imaginary part c55i as the only variable of the system with the other parameters of the model being constant, the relationship between the mechanical loss factor ηm and the electrical loss factor ηe can be obtained as depicted in Fig. 4(b). It indicates that they are in good linear relationship over a wide range too. Thus, the mechanical loss factor ηm can be indirectly achieved based on the electrical loss factor ηe.

Since admittance Ya can be tested with an impedance analyzer, the resonant frequency shift and bandwidth change of the peak are easy to obtain. Therefore, the proposed resonant system can provide a convenient means to investigate the relationships between the elastic constant c55 as well as mechanical loss factor and the shunted circuits. It should be noted that in Figs. 4(a) and 4(b), the curves deviate slightly from linearity for large variation, because the lump-parameter conditions cannot be perfectly satisfied.

4. Variation of the resonant frequency with different shunt circuits

In this section, different shunt impedance Zx’s are respectively connected to plate b to cause the shifts of the resonant frequency and the changes of the electrical quality factor, which are observed through theoretical analyses, FEM simulations and experimental tests. The relationship between the shunt impedance Zx and the resonant frequency of the system is calculated and analyzed, with the shunt impedance Zx being a resistor, a capacitor or an inductor respectively. While investigating the relationship between the shunt impedance Zx and the electrical quality factor of the resonant peak, a resistor is adopted to be the shunt impedance, as the resistance is the only means to dissipate energy and change the damping of the system.

4.1. Theoretical calculations

For the piezoelectric plates of identical thickness, different cross sectional areas of the plates will result in different matching shunt resistances, inductances and capacitances. Thus in the theoretical analyses, the product of shunt resistance and cross sectional area of the ceramic plate is defined as the shunt resistance ratio (SRR), whose unit is Ω·m2. The product of shunt inductance and cross sectional area of the ceramic plate is defined as the shunt inductance ratio (SLR), whose unit is H·m2. The quotient of shunt capacitance and cross sectional area of the ceramic plate is defined as the shunt capacitance ratio (SCR), whose unit is F/m2. With the same dimension parameters as used in Section 3: l = w = 1000 mm, tp = 2 mm, and tm = 3 mm, shunted by different SRR, SCR, and SLR, respective conductance is theoretically calculated according to Eq. (8). While calculating for SLR, an inductor is connected in series with a small resistor (0.03 m2·Ω) to simulate its inner resistance.

Several conductance curves are shown in Figs. 5(a1), 5(b1), and 5(c1) respectively. It is found that either with the increase of SRR or with the decline of SCR, the resonant frequency rises from that of short-circuit to that of open-circuit monotonically as shown in Figs. 5(a1) and 5(b1). For both cases the resonant frequency range is limited within those of short-circuit and open-circuit. However, for all SLR values, the resonant frequencies go beyond the above mentioned range limit. With the increase of the SLR, at the beginning the resonant frequency decreases from the resonant frequency of short-circuit, then at a certain SLR, it jumps to a value above that of open-circuit, and finally it declines continuously to that of open-circuit, as shown in Fig. 5(c1). Besides, it is seen from Fig. 5(a1) that the bandwidth of the resonant peak varies significantly with SRR.

Fig. 5. Electrical conductances of the system calculated from the two electrodes of wafer a by equivalent circuit method with b shunted to: (a1) a resistor (theory); (a2) a resistor (FEM); (b1) a capacitor (theory); (b2) a capacitor (FEM); (c1) an inductor in series with a resistor (0.03 Ω) (theory); (c2) an inductor in series with a resistor (0.03 Ω) (FEM).

This part introduces the materials, method and experimental procedure of the author’s work, so as to allow others to repeat the work published based on this clear description.

4.2. Simulations with finite element analysis

For verifying the theoretical analysis, the finite element method (FEM) is adopted to calculate the electrical admittance from the two electrodes of the wafer a. A three-dimensional (3D) finite element model of the system is established with ANSYS as shown in Fig. 6, where the size parameters of the system are l = w = 1000 mm, tp = 2 mm, tm = 3 mm, the same as those in theoretical calculation. The circuit element CIRCU94 is employed to build the shunt impedance connected to the wafer b. As the cross sectional area is known as Sp = lw, the resistance, capacitance and inductance connected to the wafer b is calculated according to SRR/Sp, SCR·Sp and SLR/Sp respectively. Voltage 1 V is applied to surface 1, and 0 V to surface 2. By taking harmonic response analysis, the electrical charge Q on surface 2 is picked up, and the admittance of the model is derived as

where V = 1 V and f is the frequency.

Fig. 6. The ANSYS model with the same size as that used in the theoretical analyses.

The electrical conductances calculated from the two electrodes of plate a with plate b shunted to different values of a resistor, a capacitor and an inductor in series with a resistor (0.03 Ω) are calculated. The 0.03-Ω resistor is used to simulate the inner resistance of the conductor. The curves which correspond to the same values of SRR, SCR, and SLR as those of theoretical analyses are depicted in Figs. 5(a2), 5(b2), and 5(c2), respectively. Comparing the theoretical results in Figs. 5(a1), 5(b1), and 5(c1) with the corresponding FEM curves in Figs. 5(a2), 5(b2), and 5(c2), it is found that they are matched perfectly.

4.3. Experiments verification

In order to further verify the theoretical analytical results and the finite element results, an experimental prototype resonator is fabricated as shown in Fig. 7(a). Because of limitation of the poling length, in practice the lateral dimensions of the piezoelectric plates are machined into l = w = 15 mm, far less than those used in theoretical analyses and FEM simulations. The thickness of each piezoelectric plate keeps tp = 2 mm. It is found in the study that the shape of the mass block has little influence on the resonant frequency of the system while keeping the mass constant, thus in the experiment, the mass block is machined into a round cylinder of rm = 12.5 mm and tm = 5 mm to facilitate the fabrication. Two piezoelectric plates and the mass block are bonded together with a shin layer of epoxy resin.

Fig. 7. Prototype system: (a) the sample; (b) the finite element model.

In the experiments, the conductance curves of the system with plate b shunted to different resistors, capacitors and inductors are tested by an impedance analyzer and shown in Figs. 8(a1), 8(b1), and 8(c1), respectively. Comparing Figs. 5(a1), 5(b1), and 5(c1) or Figs. 5(a2), 5(b2), and 5(c2), shows that the variation rules of the resonant frequency with different shunted circuits are in good consistence with those of the theoretical analyses and FEM simulations, while the resonant frequency range and peak bandwidth are somewhat different. The differences in the resonant frequency range and the peak bandwidth are mainly caused by the epoxy resin layer used in the experimental sample which lowers the resonant frequency of the system and provides additional damping. Moreover, the precondition of using equivalent circuit method cannot be satisfied very well, for the finite-sized experimental sample also has influences on resonant frequency and peak bandwidth, which requires the length and width to be far above thickness.

Fig. 8. Electrical conductances of the system measured from the two electrodes of wafer a by experiments with b shunted to: (a1) a resistor (experiment); (a2) a resistor (FEM); (b1) a capacitor (experiment); (b2) a resistor (FEM); (c1) an inductor (experiment); (c2) an inductor (FEM).

To verify the experimental results of the actual sample which has a finite size, a finite element model with the same size of the sample and a bonding layer is also established to conduct the simulations, as shown in Fig. 7(b). In simulations, the thickness of the epoxy resin layer is set to be 0.068 mm and the material parameters are listed in Table 1. The FEM simulation results with shunt circuits corresponding to the experiment tests are depicted in Figs. 8(a2), 8(b2), and 8(c2) respectively. It can be found that the simulation results are in good agreement with the experimental data, which means that the small size and the bonding layer of the actual experimental sample indeed make the system different from the ideal case.

5. The relationships of c55 and ηm to different shunted elements
5.1. Relationship between the variation of c55 and shunted elements

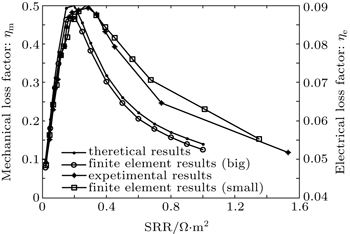
With an impedance analyzer, the conductance curves of the experimental sample are tested from two electrodes of plate a, with b shunted to different elements. The relationships between the resonant frequency of the sample and different shunted element values of a resistor, a capacitor and an inductor are measured respectively. Correspondingly, the relationships between the variations of the real part c55r of the TSM elastic constant c55 and the shunt circuits are obtained indirectly according to linear relations in Fig. 4(a).

The experimental results are shown as the curves marked with ‘*’ in Figs. 9(a)–9(c), respectively, where the results of FEM simulations of the experimental sample (of the small size: 15 mm × 15 mm) are plotted with the curves marked with ‘☐’. Moreover, for comparison, the results of theoretical analyses (curves marked with ‘•’) of the big-sized model (1000 mm × 1000 mm), as well as the results of FEM simulations corresponding to the theoretical analyses (lines marked ‘○’) are also plotted in the respective figures. It can be seen that the experimental curves, curves of the theoretical analyses, and those from the FEM simulations are all in good consistence with each other.

Fig. 9. Relationships between the elastic constant c55r and (a) SRR, (b) SCR, and (c) SLR, respectively.

From Fig. 9(a), it can be seen that the range of SRR that can change c55r is nearly from 0.01 Ω·m2 to 0.6 Ω·m2. When SRR is less than 0.01 Ω·m2, the resonant frequency of the system is almost equal to that of a short-circuit, namely , nevertheless, when SRR is larger than 0.6 Ω·m2, the resonant frequency is almost equal to that of the open-circuit, . With the increase of shunt resistance, the resonant frequency of the system increases from the resonant frequency of the short-circuit to that of the open-circuit , which means that c55r increases from the resonant frequency of the short-circuit, , to that of the open-circuit, , correspondingly. From Fig. 9(b), it can be found that the range of SCR that activates by adjusting c55r is between 10 μF/m2 and 60 μF/m2. With the growth of SCR, the resonant frequency of the system decreases from the open-circuit to the short-circuit , which means that c55r decreases from the open-circuit to the short-circuit correspondingly. Figure 9(c) shows that the relationship between fr and SLR is more complex than the above two. With the increase of SLR, the resonant frequency of the system first decreases from the short-circuit , after a jump at about 0.14 μH·m2 to a maximum value, then continuously decreases to the open-circuit , which means that c55r decreases from first, after a jump to its maximum at about 0.14μH·m2, then continuously decreases to correspondingly.

5.2. Relationship between ηm and shunted resistance

As the resistance is the only way to dissipate energy and has an effect on the damping of the piezoelectric material, the relationship between the mechanical loss factor and SRR is worth investigating. In the experiment, the conductance curves of the experimental sample are tested for different values of a resistor with an impedance analyzer. The relationship between electrical loss factor ηe and SRR is first obtained, calculated with the relative bandwidth Δf/fr. The relationship between electrical loss factor ηe and SRR is first obtained, calculated with the relative bandwidth ηm. The relationship between electrical loss factor ηe and SRR is derived indirectly according to Fig. 4(b). The experimental relationship is depicted in Fig. 10 as the line marked with ‘*’, where the relationship obtained by the FEM simulation for the experimental sample (small) is also depicted - as the curve marked with ‘☐’. It can be seen that the experimental curve and the FEM simulation curve of the sample of the same size (small) are consistent with each other perfectly. When SRR equals 0.2 Ω·m2, the shunt-damping effect is optimal. For comparison, the theoretical analysis (line marked ‘•’) and the FEM simulation (line marked ‘○’) of the big-sized model (1000 mm × 1000 mm) are also shown in Fig. 10, showing they are in good consistence with each other too. However, the small-sized sample and the big-sized model show some differences in the optimal value of SRR and the slope of the mechanical loss factor. The difference between the theoretical analysis and the experimental result is mainly caused by the small lateral dimension-to-thickness ratio and the existence of epoxy resin layer for the experimental sample, which makes the experimental sample deviate from the ideal model of the theoretical analyses.

Fig. 10. Relationships between mechanical loss factor ηm and SRR.
6. Conclusions

In this paper, we propose a coupling electro–mechanical resonant system to indirectly measure the TSM elastic constant c55 and the mechanical loss factor ηm. Based on this model, the variation of the TSM elastic constant c55 of shear-mode piezoelectric ceramic with shunt circuit is investigated through the theoretical analysis with Mason equivalent circuit, and the variations of the mechanical loss factor and the resistance with shunt circuit is also studied, which are both verified by the FEM simulations. Since the changes of the resonant frequency and the bandwidth of the peak of the conductance are easily observed, the corresponding changes of the elastic constant c55 and the mechanical loss factor ηm can be obtained indirectly.

An experiment sample is fabricated with PZT5A to test the admittance of the system with an impedance analyzer. The theoretical and simulated results are verified experimentally. The variations of the TSM elastic constant c55 and the mechanic loss factor ηm with shunt element are obtained experimentally. The relative changes of the resonant frequency and bandwidth of resonant peak with the shunt circuits experimentally show that they are in good agreement with the theoretical analyses and FEM simulations correspondingly, indicating the validity of the proposed method of measuring the variations of the TSM elastic constant c55 and the mechanic loss factor ηm of shear-mode PZT5A shunted to different circuits. It should be pointed out that the proposed coupling resonator and the obtained relationships are validated with shear-mode PZT5A (but not limited only to PZT5A).

Reference
1Forward R L 1979 Appl. Opt. 18 690
2Hagood N Wvon Flotow A 1991 J. Sound Vib. 146 243
3Lallart MLefeuvre ÉRichard CGuyomar D 2008 Sensor. Actuat. A-Phys. 143 377
4Shen HQiu JJi HZhu KBalsi MGiorgio IIsola F D 2010 Sensor. Actuat. A-Phys. 161 245
5Becker JFein OMaess MGaul L 2006 Comput. Struct. 84 2340
6Thomas ODucarne JDeü J F 2012 Smart Mater. Struct. 21 015008
7Ducarne JThomas ODeu J F 2012 J. Sound Vib. 331 3286
8Sun YLi Z HHuang A GLi Q H 2015 J. Sound Vib. 355 19
9Zhang J MChang WVaradan V KVaradan V V 2001 Smart Mater. Struct. 10 414
10Ahmadian MJeric K M 2001 J. Sound Vib. 243 347
11Guyomar DRichard TRichard C 2008 J. Intell. Mater. Syst. Struct. 19 791
12Kim J SJeong U CSeo J HKim Y DLee O DOh J E 2015 Sensor. Actuat. A-Phys. 233 330
13Kim J SLee J K 2002 J. Acoust. Soc. Am. 112 990
14Chen S BWen J HWang GWen X S 2013 Chin. Phys. 22 074301
15Corrêa de Godoy T CAreias Trindade M A 2011 J. Sound Vib. 330 194
16Benjeddou ARanger J A 2006 Comput. Struct. 84 1415
17Trindade M ABenjeddou A 2008 Comput. Struct. 86 859
18Karim YBlanze C 2014 Comput. Struct. 138 73
19Santos Heinsten F L dosTrindade M A 2011 J. Brazilian Soc. Mech. Sci. Eng. 33 287
20Benjeddou A 2001 J. Vib. Control 7 565
21Orescanin MInsana M F 2010 IEEE T. Ultrason. Ferr. 57 1358
22Fang S XTang D YChen Z MZhang HLiu Y L 2015 Chin. Phys. 24 027802
23Zhang S JJiang W HRichard JMeyer JrLi FLuo JCao W W 2011 J. Appl. Phys. 110 064106
24Behling CLucklum RHauptmann P 1999 IEEE T. Ultrason. Ferr. 46 1431
25Herrscher MZiegler CJohannsmann D 2007 J. Appl. Phys. 101 114909
26Johannsmann D 2001 J. Appl. Phys. 89 6356
27Wolff OJohannsmann D 2000 J. Appl. Phys. 87 4182
28Granstaff V EMartin S J 1994 J. Appl. Phys. 75 1319
29Sun YLi Z HLi Q H 2014 Sensor. Actuat. A-Phys. 218 105
30Luan G DZhang J DWang R Q2005Piezoelectric Transducers and ArraysBeijingPeking University Press103126103–126