† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 51571082) and China Postdoctoral Science Foundation (Grant No. 2015M580191).
Using molecular dynamics simulation method, the plastic deformation mechanism of Fe nanowires is studied by applying uniaxial tension along the [110] direction. The simulation result shows that the bcc-to-hcp martensitic phase transformation mechanism controls the plastic deformation of the nanowires at high strain rate or low temperature; however, the plastic deformation mechanism will transform into a dislocation nucleation mechanism at low strain rate and higher temperature. Furthermore, the underlying cause of why the bcc-to-hcp martensitic phase transition mechanism is related to high strain rate and low temperature is also carefully studied. Based on the present study, a strain rate-temperature plastic deformation map for Fe nanowires has been proposed.
The martensitic phase transition from body-centered-cubic (bcc) to hexagonal-close-packed (hcp) of iron (Fe) has long been a subject of great interest because of its technological and sociological importance as well as its geophysical role within the Earth core.[1–4] Half a century ago, the bcc-to-hcp martensitic phase transformation of Fe under shock-loading was first postulated by Bancroft.[5] Since then, lots of research works have been done to investigate this martensitic phase transition process. By using large-scale molecular dynamics (MD) simulations, Kadau et al. observed the evolution process of this phase transition in monocrystalline and polycrystalline Fe under shock-loading compression.[6,7] Recently, by using MD method,[8,9] the nucleation and growth mechanisms as well as morphology and growth speed of hcp domains during shock-induced phase transition of bcc Fe were studied in depth. These simulation results were further confirmed by in-situ x-ray diffraction and ex-situ transmission electron microscopy experiments.[3,10] However, we notice that all of the above works were devoted to the bcc-to-hcp martensitic phase transformation of Fe under shock-loading compression; so we cannot help asking that whether the bcc-to-hcp martensitic phase transformation can be realized under tension.
The properties of nanowires were studied by many authors,[11–13] in the present paper we focused on the plastic deformation mechanisms of metal nanowires. As we all know, strain rate is an important factor that can affect the plastic deformation mechanisms of metal nanowires. At low strain rate, plastic deformation mechanisms of metal nanowires are dominated by dislocation mechanisms;[14–16] however, at high strain rate, Ikeda[17] and Branício et al.[18] found Ni and NiCu nanowires could transform continuously to an amorphous phase. This phenomenon is known as momentum-induced melting, which has also been confirmed by experiments.[19–21] In our previous work,[22] the plastic deformation mechanism of Cu nanowires was studied by using molecular dynamics simulation method, and it was found that a new fcc-bcc-hcp phase transformation mechanism controlled the plastic deformation of the nanowires at low temperature and high strain rate. Inspired by these works, we speculate that the strain-rate-induced bcc-to-hcp martensitic phase transformation of Fe may take place under tension. So in the present work, we will carefully study the effect of strain rate on the plastic deformation mechanism of Fe nanowires under tension by using molecular dynamics method. Our simulation result shows that the bcc-to-hcp martensitic phase transformation will take place with increasing strain rate.
The MD simulations are conducted with a parallel MD code, LAMMPS, which was developed by Plimpton and co-workers.[23,24] Fe [110] nanowires with a nearly square cross section and surface orientations of [1
The embedded-atom (EAM) potential[30] is employed in this study. This potential provides a good qualitative agreement with a large body of experimental and ab initio calculation data for Fe, including the elastic modulus, the energy of point defects, the phase transition energy, the lattice parameter of bcc iron for several temperatures, the density of structure factor of the liquid phase, and the melting temperature.[31] The simulation results are visualized using the common neighbor analysis method (CNA) as described in Ref. [32] and implemented in the OVITO program.[33]
Figure
 | Fig. 1. The normal stress σxx along the tension direction as a function of the tensile strain for Fe nanowires at 100 K. |
The two typical deformation modes of nanowires are presented in Fig.
Figure
 | Fig. 3. The normal stress σxx along the tension direction as a function of the tensile strain for Fe nanowire at strain rate 5 × 109 s−1. The applied temperatures range from 5 K to 300 K. |
Based on the above study, it can be found that the plastic deformation mechanism of the nanowires is related not only with strain rate but also with temperature. When temperature reduces to 5 K, even the strain rate is as low as 1 × 108 s−1, the plastic deformation mechanism of the nanowires is still controlled by bcc-to-hcp phase transformation mechanism rather than dislocation nucleation mechanism. The simulation results have confirmed our early speculation that the bcc-to-hcp martensitic phase transformation of iron can be realized under tension load. Moreover, the simulation results also manifest that the high strain rate and low temperature are all in favour of the bcc-to-hcp martensitic phase transformation. To gain a deep understanding of the strain-rate-induced bcc-to-hcp martensitic phase transformation of iron nanowires, the following two questions must be answered: (i) which kind of mechanism controls the bcc-to-hcp martensitic phase transition. (ii) Why is the bcc-to-hcp martensitic phase transition mechanism related to high strain rate or low temperature?
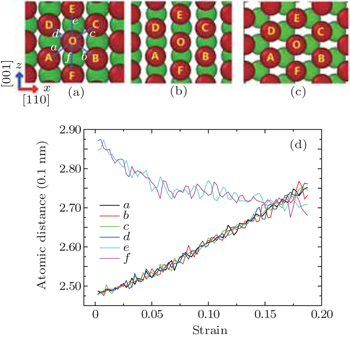
In this part, we will answer the first question. Figure
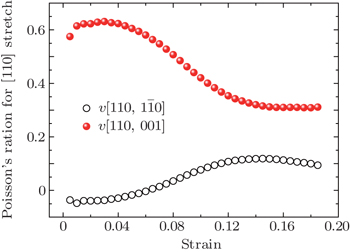
We noticed that this bcc-to-hcp martensitic phase transition mechanism is identical to the martensitic phase transition mechanism during shock compression of Fe along [001] direction;[6] this is to say that compressing the Fe along [001] direction has the same effect as stretching it along [110] direction. This interesting and important phenomenon can be understood by considering the unique Poisson’s ratio of iron for [110] stretch. Figure
In the following part, we will answer the question why the bcc-to-hcp martensitic phase transition is related to high strain rate or low temperature. The energy barrier of the bcc-to-hcp martensitic phase transition process is calculated using a so-called induced energy minimization method (IEM)[35,36] and displayed in Fig.

 | Fig. 6. The potential energy per atom as a function of reaction coordinates during the bcc-to-hcp phase transformation. |
It is well known that the dislocation nucleation from the free surface of the nanowire is a thermal activation process. Zhu[16] has developed an atomistic modeling framework to address the probabilistic nature of surface dislocation nucleation, which shows that the activation volume associated with surface dislocation nucleation is characteristically in the range of 1 − 10b3 (b is the Burgers vector). Such small activation volume leads to sensitive temperature and strain-rate dependence of the nucleation stress (the maximum stress of the stress–strain curve). Within the linear approximation of stress-dependent activation energy, the dislocation nucleation stress (or the elastic limit stress on the strain–stress curve) is given by equation:[16]
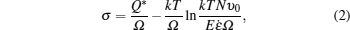


The Fe nanowires have two plastic deformation mechanisms for a [110] stretch, namely, the dislocation nucleation mechanism and the bcc-to-hcp martensitic phase transformation mechanism. If the elastic strain energy reaches the energy barrier for the martensitic phase transition, the bcc-to-hcp martensitic phase transformation mechanism will control the plastic deformation of the nanowires; otherwise, the dislocation nucleation mechanism will work.
Figure
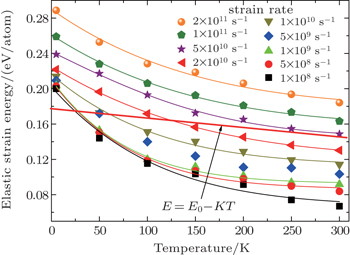 | Fig. 7. The maximum value of the elastic strain energy as a function of temperature under different strain rates. |
Furthermore, from Fig.
In summary, the plastic deformation mechanism of Fe nanowires is studied using molecular dynamics simulation method by applying uniaxial tension along the [110] direction at constant strain rate and temperature. The simulation results show that at high strain rate or low temperature, the bcc-to-hcp martensitic phase transformation mechanism controls the plastic deformation of the nanowires; however, at low strain rate and high temperature the plastic deformation mechanism will transform into a dislocation nucleation mechanism. It is found that this bcc-to-hcp martensitic phase transition mechanism is identical to the bcc-to-hcp martensitic phase transition mechanism during shock compressing Fe along [001] direction, and the underlying reason can be attributed to the unique Poisson’s ratio of iron for [110] stretch. Furthermore, the underlying cause of why the bcc-to-hcp martensitic phase transition mechanism is related to high strain rate and low temperature is also carefully studied, and based on the study a strain rate–temperature plastic deformation map for iron nanowires has been proposed; this map shows a vivid story about the transition between the two different plastic deformation mechanisms, and will help us develop in-depth understanding of the plastic deformation of Fe nanowires.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 |