Tropical cyclones are one of the most common weather conditions that occur over the tropical oceans. When the sustained wind speed reaches at least 34 meters per second, a tropical cyclone is called “typhoon” in the Northwestern Pacific or “hurricane” in the North Atlantic or Northeastern Pacific. Typhoons are one of the most destructive natural disasters. Although satellites can effectively detect and track typhoons, it is difficult to measure the wind speed accurately. An alternative approach is to use the reconnaissance aircraft. However, this approach is severely limited due to the expense of these aircraft. Hence, it is urgent to develop new methods to monitor typhoons accurately and inexpensively.

Ocean noise provides a practical means to study typhoons. Previous works^[1–3] show that the summation of noise intensity within a circularity area above the receiver dominates the noise intensity, and hence we can roughly estimate the power of typhoons safely and inexpensively by measuring underwater noise intensity. However, we need experimental data to support the theory. In addition, it is presented in the literature that the local (within a few kilometers) wind speed is the dominant factor for the noise intensity, but this claim still needs to be further verified.

Basic concepts and characteristics of ocean noise should be understood before it is applied to monitor typhoons. Ocean noise is an important research area in underwater acoustics. It is well known that ocean noise originates from multiple sources, including wind-generated sources, biological sources, shipping sources, etc., and no one type of sources dominates the received field in most situations.^[4] Wenz curve published in 1962 is one of the most important works on ambient noise, which presents the feature of noise spectral intensity for sources such as earthquakes, ships, and winds in a broad frequency band in the deep ocean.^[5] The noise summary curve is the basis of many prediction systems. An overview and perspective on the subject of underwater ambient noise was provided by Dahl,^[4] which discussed particularly the approximate magnitude and frequency dependence of underwater ambient noise and a partial inventory of its primary sources.

Wind-generated noise is an essential component of underwater ambient noise.^[6] A number of wind-generated noise models have been proposed based on different physical mechanism assumptions. One prediction model for ambient noise levels is developed by Tkalich and Chan under the assumption that the acoustic power is radiated by a bubble cloud under breaking wind waves.^[7] Deane and Stokes presented a model for the underwater noise of whitecaps by assuming that the noise from a few hundred hertz to 80 kHz is due to the pulses of sound radiated by bubbles formed within a breaking wave crest.^[8] Another theory proposed by Wilson is that the physical mechanism of the wind-induced noise should involve the impact of water droplets from ocean spray, streaks, and whitecaps, which largely depends on the wind speed.^[9] He also developed a wind-generated noise model based on the “whitecap index,” a function describing the coverage degree of “whitecaps” due to different wind speeds. This model allows for a separate estimate of distant storm noise and local wind noise.^[10,11] Kuperman and Ingenito proposed a widely used noise model based on the normal mode theory to calculate the ocean noise field with a uniform ocean noise source distribution.^[12]

The above-mentioned models have been verified by lots of experimental data in different environments. Ferguson and Wylline calculated the theoretical response of a conventional beamformer using various noise models which take into account distributions of surface or volume sources. The theoretical response is then compared with the observed response for noise generated by winds and waves at the ocean surface. Good agreement is obtained when the wind-generated noise is modeled as a uniform distribution of dipole sources.^[13] High correlation between the wind speed and the ambient noise intensity is observed at both low frequencies (tens of hertz) and higher frequencies (hundreds of hertz) by using correlation techniques.^[14–18] Low frequency ambient noise at deep ocean sites are measured and the power-law wind speed dependence is summarized by Chapman and Cornish.^[19] However, when investigating the relationship between the local winds and the noise intensity experimentally, it is difficult to eliminate the effects of local contaminating (non-surface wind-generated) noise sources.

In the frequency range of interest in this paper, which is in the range of 100 Hz–1000 Hz, shipping and winds are considered as two major sources of ocean noise. Usually, the high shipping density nearby makes it difficult to observe the effect of winds in experiments with a single omnidirectional hydrophone. However, during a typhoon, wind-generated sea surface agitation provides the dominant contribution to the ambient noise field due to the low shipping density within the storm region. Even more fortunately, the wind speed changes dramatically during a quite short period of time (usually two or three days), which is a desirable situation to investigate the wind-generated noise.

Very few papers have been published on data/model comparison about the typhoon-generated noise. In this paper, a model is developed for the noise intensity due to a typhoon in an ocean waveguide. Experimental data are then analyzed with this model. The results show the potential to study typhoons by ocean noise.

A typhoon is a mature tropical cyclone that develops in the northwest Pacific ocean. The near-surface wind field of a typhoon is nearly axisymmetric. The wind speed is low at the center, but it increases rapidly with range to its maximum value, and then decays gradually with range, as shown in Fig. 1. Therefore, the typhoon wind field can be divided into three regions: (i)

eye: the center of the typhoon, where the wind speed is low;

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Satellite image of typhoon “Krosa” (2013/11/02  03:00 (UTC)). This figure is from the Digital Typhoon Web page of National Institute of Informatics (NII), Japan.

The wind speed of a mature typhoon is described by a parametric cyclone model developed by Holland,^[20] which is expressed as

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The simulated wind speed profile using Holland’s model.

Table 1.

Table 1.

Table 1. Simulation parameters. . A B pn/hPa pc/hPa ρa/(kg/m3) 12.5 1.0 1008 965 1.15

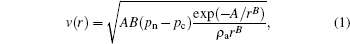
Table 1. Simulation parameters. .

In the frequency range of 100 Hz–1000 Hz, shipping and wind noises are two major components of the noise field. Fortunately, the ship density during a typhoon is small such that the contribution of shipping noise is almost negligible.

The geometry of the typhoon-generated noise model is shown in Fig. 3. Under the assumption that the monopole sources are uncorrelated, for a single receiver at (r,z), the received noise intensity radiated from (r_s,z_s) is written as^[21]

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The geometry of the typhoon-generated noise problem (not to scale). Monopole sources agitated by typhoon are located at the plane marked with the points beneath the sea surface. The arrow indicates the path of the typhoon center, and a single receiver is deployed at the origin.

In a range-independent waveguide, the Green’s function can be expressed as the summation of normal modes,

By substituting Eq. (4) into Eq. (2) and neglecting the coherent terms, the noise intensity can be expressed as

Equation (5) can be further approximated as

If the typhoon eye is far away from the receiver, the wind speeds within a disc centered at the receiver vary little with spatial position, so equation (6) reduces to the derivation in Ref. [23],

Equations (6)–(8) imply that different factors dominate the noise field, depending on the distance between the receiver and the typhoon. Specifically, if the receiver is far away from the eye, the wind speed directly above the receiver, referred to as the local wind speed, is dominant; however, if the receiver is close to the eye, the average wind speed is dominant.

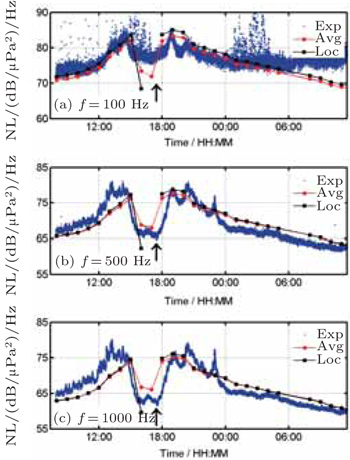
To verify the feasibility of the theory model, typhoon-generated noise data collected during an experiment are analyzed in the 100 Hz–1000 Hz frequency band as typhoon “Krosa” passed over a hydrophone from October 31, 2013 to November 2, 2013. The hydrophone was deployed at 1030m with a water depth of around 3.8 km. Figure 4(a) shows the range from the center of the typhoon to the hydrophone.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (a) Distance from the typhoon center to the receiver; (b) NL at 100 Hz, 500 Hz, and 1000 Hz.

Typhoon “Krosa” passes the receiver almost overhead, only 3 km away from the receiver, and the eye wall of the typhoon passes over the receiver and cuts a swash through the whole storm. The measured acoustic intensity at 100 Hz, 500 Hz, and 1000 Hz as shown in Fig. 4(b) exhibits a temporal pattern marked by an initial maximum, followed by a minimum, and then a final maximum, which is referred to as the “bi-peak” structure in this paper. This variation is consistent with the advection of the characteristic morphology of a typhoon over a hydrophone, with the first sound intensity maximum corresponding to the high-speed winds in the leading-edge of the eye wall, the minimum to the low-speed winds in the eye, and the final maximum to the high-speed winds in the trailing edge of the eye wall. It is observed that this “bi-peak” structure is more significant at higher frequencies than at lower frequencies. At 100 Hz, the intensity decreases from 87 dB at the left peak to 80 dB at the trough, and then goes up to 87 dB at the right peak, yielding a 7-dB peak-to-trough difference. At 1000 Hz, it drops from 83 dB to 66 dB and then ascends to 82 dB, yielding a 17-dB peak-to-trough difference. Thus, it is evident that the typhoon-generated noise has a greater influence on ocean ambient noise at higher frequencies than at lower frequencies.

Predictions from both two approximations(the average wind speed approximation and the local wind speed approximation) are compared with measured noise intensities in Fig. 5, which shows that the average wind speed approximation has a better performance on predicting the noise intensity when the eye is close to the receiver, and both approximations yield good predictions when the typhoon center is far from the receiver. The maximum deviation occurs when both the eye wall and the eye are close to the receiver due to dramatic changes in the wind speed.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Noise spectral intensity levels at (a) 100 Hz, (b) 500 Hz, and (c) 1000 Hz. The dash lines with circles and squares correspond to Eqs. (6) and (8), respectively. The arrow denotes the time when the typhoon center passed closest to the receiver.

Figure 5 also shows that the deviation increases with decreasing frequency, which might be attributed to the complex components of ambient noise at low frequencies, for instance, sound from distant sources, or some other mechanisms that are completely irrelevant to typhoons. On the contrary, the ambient noise at high frequencies can be treated as relatively pure typhoon-generated noise with no ships around or sound from distant sources.

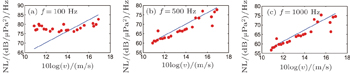
Statistic analysis of intensities at peaks and off-peaks is carried out to demonstrate the wind and frequency dependence.

The logarithm of noise intensity for experimental data versus 10log₁₀f at the peak and the off-peak point is exhibited in Fig. 6. It is evident that the noise intensity is approximately proportional to f^−0.85 (see Eq. (3)) from 300 Hz to 2000 Hz (within the frequency band of wind-generated noise), which is obtained by fitting the experimental data to the model.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. The frequency dependence of the noise spectral intensity level.

In Ref. [23], there is a power law relationship between the local wind speed and the underwater noise intensity, written as

Figure 7 depicts the relationship between the noise spectral intensity level (NL) and the logarithm wind speed at 100 Hz, 500 Hz, and 1000 Hz. The local wind speed is determined by Holland’s model and the information issued by JMA (Japan Meteorological Agency), such as the maximum wind speed, the radius at maximum speed, and the central pressure. Figure 7 shows that the noise intensity is proportional to the logarithm of the local wind speed with a slope of n = 3 on the whole, consistent with the results of Ref. [23]. At 100 Hz, there seems no discernible correlation-ship between wind speed and NL when v < 10^1.4 m/s, however, their relation gets better as wind speed rises. The composite of ambient noise spectra presented in Ref. [5] gives an interpretation of the phenomena. The wind-dependent bubble and spray noise dominate at high frequencies (> 300 Hz), while the shipping noise dominates in the intermediate region from 10 Hz to 300 Hz. The noise intensity of 100 Hz in Fig. 7(a) has little correlation with log v at low wind speeds (< 101.4 m/s) because the wind-generated noise sources are not the dominant noise source. With the wind speed and the frequency rising, the wind-generated noise sources dominate the noise generation process. Furthermore, the linear relationship between NL and the local wind speed becomes more significant at higher frequencies.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Data/model comparison of the wind dependence for frequencies at (a) 100 Hz; (b) 500 Hz, and (c) 1000 Hz.

In summary, an analytical typhoon-generated noise model is developed in this paper. It is concluded that when the eye is far away from the receiver, the local wind speed is the dominant factor for the typhoon-generated noise intensity; however, when the eye is near the receiver, the average wind speed becomes dominant. Experimental data gathered during a typhoon were processed to validate the present model. The data/model comparison indicates that the typhoon has a greater impact on the noise spectral level at high frequencies than at low frequencies in the frequency range of 100 Hz–1000 Hz. The “bi-peak” structure is observed from experimental data, and is explained by the present model. Experimental data analysis supports the frequency dependence assumption, with the index p = −0.85. The power-law wind speed dependence is also verified by comparing experimental data and predicted data with n = 3. The preliminary evaluation of 500 Hz and 1000 Hz shows reasonable agreement between the model and experimental data. However, much more extensive prediction evaluations for more experimental data sets are required to verify the present model.