Magnetism of nanoparticles is interesting and is currently under extensive investigation.^[1] The exchange bias (EB) effect, referring to a shift of the ferromagnetic hysteresis loop along the field axis by an amount of H_E, which was first discovered in 1956 by Meiklejohn and Bean in fine particles of cobalt with a cobaltous oxide shell,^[2] is gaining increased interest regarding its fundamental interest as well as potential applications, such as domain stabilizers in magnetoresistive heads and spin-valves.^[3–5] In particular, both the core–shell systems with a ferromagnet (FM) core and an antiferromagnet (AFM) or a ferrimagnet (FIM) shell which could be obtained from an oxidation of transition metal nanoparticles, and the so-called “inverted” core–shell systems with an AFM core and a FIM shell, e.g., MnO/Mn₃O₄,^[6,7] MnO/Mn₂O₃,^[8] and Mn/Mn₃O₄,^[9] have come into focus for the study of the EB effect resulting from the exchange coupling between the core and the shell.^[10] Usually, the core and the shell correspond to two different magnetic materials in the core–shell nanoparticles systems. In addition to the FM/AFM and AFM/FIM interfaces, EB has also been observed in other types of interfaces involving a spin glass (SG) phase (e.g., FM/SG).^[11–14] It is a common understanding that the uncompensated spins on the surface of the magnetic nanoparticles may result in a low-temperature SG phase.^[15] However, particle systems may also exhibit the SG-like behavior due to the dipolar interactions between the particles according to the Stoner–Wohlfarth model.^[16,17] Karmakar et al. argued that the low temperature SG state is very sensitive to the field and the degeneracy of the SG state can be reduced depending on the strength of the cooling field (H_FC).^[14] In some cases, the SG behavior can exist under high H_FC.^[13]

In this paper, we report an existence of a SG surface layer and a strong EB effect in single phase Mn₃O₄ nanoparticles with an average size of about 30 nm, 60 nm, and 90 nm. A detailed investigation of the frequency dependence of the ac susceptibility and Henkel plot for the Mn₃O₄ nanoparticles has been made, and the origin and nature of the observed EB have been elucidated. Our study suggests that the occurrence of the EB can be attributed to the pinning effect of the frozen SG surface layer upon the FIM core.

Single phase Mn₃O₄ nanoparticles with an average size of about 30 nm, 60 nm, and 90 nm were prepared by an auto-combustion method using analytical grade metal nitrate (Mn(NO₃)₂·6H₂O) as the metal ion source, ethylene glycol (C₂H₆O₂), citric acid (C₆H₈O₇), and urea (CO(NH₂)₂) as the fuels, respectively.^[18,19] Mn(NO₃)₂·6H₂O and the fuel were dissolved in de-ionized water and mixed in an appropriate ratio to form the precursor solution. The mixed precursor solution was concentrated by heating until the excess free water was evaporated and spontaneous ignition occurred. The combustion finished within a few seconds and the resultant ash was collected. The ignition temperature has a significant influence on the particle size of the product, i.e., the particle size increases with the increase of the ignition temperature.^[19] X-ray diffraction showed that the synthesized sample is single phase with a tetragonal space group I4₁/amd (No. 141).^[19] Magnetic properties were measured on a physical properties measurement system (PPMS 9 T, Quantum Design).

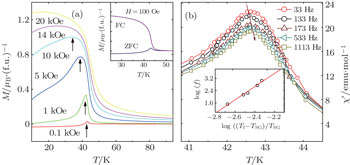
The temperature dependences of magnetization after zero-field cooled (ZFC) and field cooled (FC) processes are shown in the inset of Fig. 1(a) for the 60 nm Mn₃O₄ particles under an applied field of 100 Oe. The transition to the long-range FIM order at about 45 K (T_C) is clearly demonstrated. T_C of the nanoparticles is higher than the Curie temperature of bulk Mn₃O₄ (T_C = 42 K).^[20] A peak is observed at T_p ≈ 43 K on the ZFC curve, and the magnetization shows a sharp decrease below T_p as the temperature decreases. To understand the nature of the magnetic behavior around T_p, we have measured ZFC magnetization (MZFC) under different fields as shown in Fig. 1(a). The peak position of magnetization is significantly affected by the applied measurement field up to ∼ 20 kOe and shifts to a lower temperature with the increase of the measurement field. A sharp decrease of MZFC occurs around T_p ≈ 35 K under the measurement field of 10 kOe, whereas no decrease of MZFC is shown under 20 kOe down to 10 K. MZFC under different fields for two other samples with the average sizes of 30 nm and 90 nm are also measured (not shown). Under the same applied field, T_p increases with the particle size decreasing.^[19] Such a strong magnetic field dependence of T_p and the large magnetic irreversibility between MFC and MZFC below T_p (inset in Fig. 1(a)) may indicate a frustrated magnetic state.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. (a) ZFC magnetization (MZFC) versus temperature under different fields for 60 nm Mn3O4. Tp represents the peak temperature. The inset shows ZFC and FC magnetization versus temperature under 100 Oe. (b) Temperature dependence of the ac susceptibility for different frequencies of 33 Hz, 133 Hz, 533 Hz, 1113 Hz at a driving ac field of 15 Oe for 60 nm Mn3O4. The inset shows logf versus log[(Tf − TSG)/TSG], demonstrating the agreement with Eq. (1). The solid line displays the best fitting result.

The ac susceptibility versus temperature for the 60 nm Mn₃O₄ particles, i.e., χ′(T), is shown in Fig. 1(b). A frequency dependent maximum is observed at T_f, close to T_p on the ZFC magnetization curve. The peak shifts toward higher temperature and χ′(T) decreases as the frequency increases. The frequency dependence of T_f can be well described by the conventional critical “slow down” of the spin dynamics as^[21]

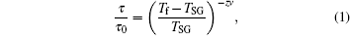
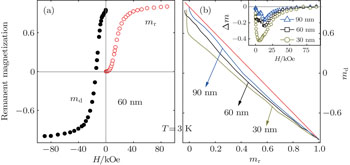
For an assembly of magnetic nanoparticles, the above SG behavior may also be associated with the dipolar interactions between the particles according to the Stoner–Wohlfarth model.^[16,17] The interparticle interaction could be illustrated by the Henkel plot according to the Wohlfarth relation.^[26] The DC demagnetization (DCD) remanence curve M_d(H) is traced by taking initially the system to saturation, after that, the field is taken to a negative value of –H. The full curve is traced by repeating this procedure with negative fields of increasing amplitude up to the field of the same modulus as the initial saturation field. The isothermal remanent magnetization (IRM) curve M_r(H), on the other hand, is obtained by starting from a demagnetized sample (to be subjected to an ac demagnetization) and measuring the remanence for increasing fields up to H_sat (85 kOe). The measured IRM and DCD remanence curves for the 60 nm particles are shown in Fig. 2(a), which represents the variations of M_r and M_d with the applied field. The Henkel plots are obtained for the sample by plotting the normalized demagnetization remanence m_d(H) = M_d(H)/M_r (85 kOe) as a function of the normalized isothermal remanent magnetization m_r(H) = M_r(H)/M_r (85 kOe). In Fig. 2(b), we present m_d versus m_r for the three samples with the sizes of 30 nm, 60 nm, and 90 nm, respectively. Also shown in Fig. 2(b) is the Wohlfarth relation m_d = 1 − 2m_r corresponding to noninteracting single-domain particles or domain walls in continuous media moving through a fixed distribution of pinning sites.^[26] The deviation from the Wohlfarth relation indicates significant interaction between the particles. Furthermore, the Δm (= m_d − (1 − 2m_r)) plot as a function of the applied field is shown in the inset of Fig. 2(b). This plot would be a horizontal line through the origin if there were no interactions between the particles.^[27] The negative Δm implies that the dipolar interaction between the particles makes it difficult to magnetize the sample from the ac demagnetized state.^[28] The maximum magnitude of Δm indicates the dipolar interaction strength. If the observed SG behavior in the Mn₃O₄ nanoparticles was due to the dipolar interactions between the particles, the interaction should increase with the particle size based on the simple model.^[29] On the contrary, the dipolar interaction strength seems to decrease with the increase of the particle size as shown in Fig. 2(b), which strongly suggests that the dipolar interaction is not responsible for the observed SG behavior. Furthermore, the saturation magnetization (M_S) of the nanoparticles decreases from 1.71 μ_B/f.u. to 1.51 μ_B/f.u. as the particle size decreases at 14 K (the M_S of Mn₃O₄ bulk material is about 1.5 μ_B/f.u. at 34 K).^[19] Therefore, the SG behavior could be reasonably attributed to the surface spins disorder. As the particle size decreases, the surface/volume ratio increases and the SG behavior reinforces. The reason for the formation of the surface spin disorder is not clear yet, but broken bonds or the translational symmetry breaking of the lattice at the surface may generate such a disorder.

As mentioned above, EB has been observed in some systems containing FM/SG interfaces.^[11–13] Therefore, it would be interesting to explore if EB exists in the Mn₃O₄ nanoparticles containing FIM/SG interface. Figure 3(a) shows the hysteresis loops of the 60 nm Mn₃O₄ particles at 10 K after ZFC or FC process. For the ZFC process, the sample was cooled in zero magnetic field from 300 K to 10 K. For the FC process, the sample was cooled in a magnetic field of 10 kOe from 300 K to 10 K. Thereafter, the hysteresis loops were measured between ±20 kOe. As shown in Fig. 3(a), the FC hysteresis loop shifts to the negative field direction and the positive magnetization direction, indicating the existence of EB, while the ZFC loop is symmetric around the origin. The EB field or the offset of the hysteresis loop along the field direction, H_E, is determined using the relation H_E = (H₊ + H₋)/2, where H₊ and H₋ are the fields corresponding to the loop crossing the M = 0 axis on the ascending and descending branches of the M–H loop.^[30] During cooling the Mn₃O₄ nanoparticles in FC mode, a preferred orientation is imposed upon the surface spins in the SG state, while the FIM core, with a higher ordering temperature, is polarized as a single domain. When the field is removed, the FIM core experiences a field generated by the frozen spins in the surface layer in the direction of the previously applied field, generating the observed offset of the hysteresis loop. The inset of Fig. 3(a) shows H_E versus the particle size. The offset of the hysteresis loop increases with the size decreasing as shown in the inset of Fig. 3(a) because of the increased surface/volume ratio. The temperature dependence of H_E and H_C (H_C = (H₊ − H₋)/2) is shown in Fig. 3(b). H_E sets in at T ∼ 35 K, which is below the SG transition temperature T_p ≈ 43 K, because H_E can only exist when the anisotropy of the frozen surface SG layer with a preferred orientation is large enough and can hinder the switching of the FIM core spins during the demagnetization process. On the other hand, figure 3(b) clearly shows that a strong increase in H_C occurs just below T_p, implying a close relation between H_C and the freezing of the surface SG. Therefore, the increase of the coercivity can be attributed to the extra energy required for the switching of the spins that are pinned by the exchange interactions with the frozen SG surface layer.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) Normalized DC remanent magnetization md(H) and normalized isothermal remanent magnetization mr(H) for 60 nm Mn3O4 at 3 K. (b) md(H) versus mr(H) for 30 nm, 60 nm, and 90 nm Mn3O4 nanoparticles at 3 K. Inset shows the behavior of Δm(H) at 3 K.

Fig. 3.

	Figure Option ViewDownloadNew Window
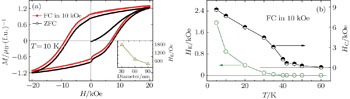	Fig. 3. (a) Magnetic hysteresis loops of Mn3O4 at 10 K measured after ZFC and FC in 10 kOe field. Inset: particle-size dependence of HE at 10 K. (b) Temperature dependence of HE and HC.

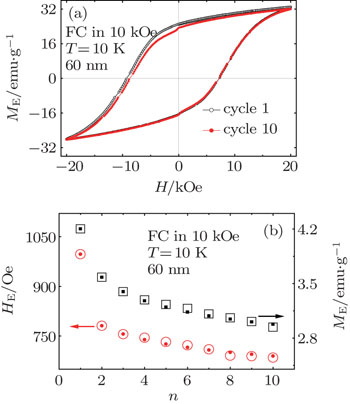
One of the important properties in the EB systems is the training effect, which describes a gradual decrease of H_E when the system is continuously cycled through several consecutive hysteresis loop measurements.^[16] The consecutive hysteresis loops were measured at T = 10 K after field cooling in 10 kOe. The first and the tenth loops for the 60 nm Mn₃O₄ particles are shown in Fig. 4(a). The training effect is obviously present in our sample. Both the exchange-bias field and the magnetization shift decrease with magnetic field cycling. The number (n) of field cycles dependence of the H_E and the magnetization shift M_E is shown in Fig. 4(b) (open circles and squares, respectively). For the training effect in FM/AFM heterostructures and within the framework of nonequilibrium thermodynamics, it was proposed that consecutively cycled hysteresis loops of the FM top layer trigger the spin configurational relaxation of the AFM interface magnetization toward equilibrium, and a recursive formula can be obtained describing the n dependence of H_E (M_E)^[31]

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (a) Training effect of EB for 60 nm Mn3O4. The first and the tenth loops at 10 K after FC in 10 kOe field are plotted. (b) The number (n) of field cycles dependence of HE and ME (open symbols). The solid symbols show the data generated from the recursive sequence in Eq. (2) as described in the text.

Table 1.

Table 1.

Table 1. Parameters obtained from the best-fitting to the experimental data with Eq. (2). . 30 nm 60 nm 90 nm HE∞/Oe 1086 575 273 ME∞/emu·g−1 2.238 2.319 2.339 γH/10−6Oe−2 0.487 2.887 7.629 γM/emu−2·g−2 0.069 0.093 0.241

Table 1. Parameters obtained from the best-fitting to the experimental data with Eq. (2). .

For further revealing the origin of the EB effect in Mn₃O₄, we studied the H_FC dependence of the EB at 10 K. The M–H loops were measured between ±20 kOe after the sample was cooled under different fields from 300 K to 10 K. As shown in Fig. 5(a), H_E increases sharply with the increase of H_FC, then approaches to a saturation for H_FC higher than 10 kOe. It is surprising that the state is stable for the H_FC up to 70 kOe, which is similar to the report on the La_0.2Ce_0.8CrO₃ nanoparticles,^[13] but is in contrast to the observations in systems involving SG phases, which typically show a decrease of H_E for large H_FC.^[14,32] Figure 5(a) also shows that H_E increases with the decrease of the particle size as expected due to the higher surface/volume ratio. As shown in Fig. 5(b), M_E presents a similar trend to H_E with the variation of H_FC.^[33] When the applied cooling field is below 10 kOe, the frozen spins of the SG state may not be entirely along the magnetic field direction, exhibiting weak unidirectional anisotropy and providing a weak pinning force during the magnetization reversal. As H_FC increases, the frozen spins of the SG state are along the magnetic field direction and saturate gradually, exhibiting strong unidirectional anisotropy and providing a strong pinning force to maintain the magnetization. As shown in Fig. 1(a), the peak of the ZFC curve disappears under high field (> 10 kOe), which indicates that the frozen SG state melts and the spins on the surface are along one direction. It is easy to understand that the pre-aligned frozen spins of the SG state play a critical role in the induction of H_E. Therefore, we can conclude that EB can be attributed to the pinning effect of the frozen surface spins upon the FIM core.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (a) HE verus HFC at 10 K for 30 nm, 60 nm, and 90 nm Mn3O4. (b) ME dependence of HE at 10 K.

In summary, we have observed spin glass behavior and EB phenomena in Mn₃O₄ nanoparticles. The dynamics scaling analysis of the ac susceptibility and the Henkel plot suggest that the observed SG behavior can be readily understood by taking into account the formation of surface spin glass due to the existence of broken bonds and the break of the translational symmetry of the lattice. The exchange bias field of the Mn₃O₄ nanoparticles shows a strong dependence on the temperature, strength of cooling field, as well as particle size. Below the SG freezing temperature T_p, H_E increases with temperature decreasing. H_E increases sharply with the cooling field H_FC for H_FC < 10 kOe and approaches to a saturation for larger H_FC (> 10 kOe). H_E increases as the particle size decreases due to the increased suface/volume ratio and the enhanced surface spin disorder. In addition, the observed training effect of the EB behavior has been explained well in terms of the existing relaxation model. These results imply that the existence of EB Mn₃O₄ nanparticles can be attributed to the pinning effect of the frozen SG surface layer upon the FIM core.