† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant Nos. 2011CB921803 and 2012CB921704), the National Natural Science Foundation of China (Grant Nos. 11174035, 11474025, 11404090, and 11674026), the Natural Science Foundation of Hebei Province, China (Grant No. A2015205189), the Hebei Education Department Natural Science Foundation, China (Grant No. QN2014022), and the Specialized Research Fund for the Doctoral Program of Higher Education, China.
Topological insulators/superconductors are new states of quantum matter with metallic edge/surface states. In this paper, we review the defects effect in these topological states and study new types of topological matters — topological hierarchy matters. We find that both topological defects (quantized vortices) and non topological defects (vacancies) can induce topological mid-gap states in the topological hierarchy matters after considering the superlattice of defects. These topological mid-gap states have nontrivial topological properties, including the nonzero Chern number and the gapless edge states. Effective tight-binding models are obtained to describe the topological mid-gap states in the topological hierarchy matters.
Topological matters including topological insulators (TIs) and topological superconductors (TSC) have become active research fields in condensed matter physics.[
Topological quantum states are robust against local perturbations. From the “holographic feature” of the topological ordered states, people may use the topological defects such as the quantized vortices with half of magnetic flux Φ0 = hc/2e and the crystal dislocations to probe the non-trivial bulk topology of the system.[11,12] In two-dimensional (2D) Chern insulators or in 2D topological superconductors, a π-flux (quantized vortex) induces mid-gap (MG) zero energy states (zero modes).[11,12] For 2D D-type topological superconductors, the Majorana fermionic zero modes localize around the quantized vortices. In addition, non-topological lattice defects (for example, vacancies) may also induce zero modes in a topological matter with spectrum symmetry.[13]
When there are two defects (quantized vortices or vacancies) nearby, the inter-defect quantum tunneling effect occurs and the fermionic zero modes on the two defects couple. For multi-topological-defect that forms a superlattice, there may exist mid-gap bands. It has been pointed out that in TIs/TSCs, for multi-vortex that forms a two dimensional superlattice on topological matters, due to the polygon rule (each Majorana/fermion gains an accumulated phase shift |ϕ| = (n − 2)π/2 when encircling a smallest n-polygon[14]), the defect-induced mid-gap states can be regarded as an emergent “TIs/TSCs” with nontrivial topological properties, including the nonzero Chern number and the gapless edge states.[15–17] For a topological insulator with spectrum symmetry, we also found that the vacancy-superlattice induces topological mid-gap states and the low-energy physics of the localized modes become that of an emergent “TI” on the parent TI.
In this review, we call these composite topological matters with superlattice of defects a topological hierarchy insulator or topological hierarchy superconductor. We then summarize the quantum properties of the topological hierarchy insulator and those of the topological hierarchy superconductor. In Section 2, we review the topological hierarchy superconductor induced by superlattice of quantized vortices and study the topological properties of the mid-gap states. In Section 3, we review the topological hierarchy insulators induced by superlattice of quantized vortices and those induced by the vacancy-superlattice. Finally, we give the conclusion and outlook in Section 4.
In this section we will review the topological hierarchy superconductors. We take the s-wave pairing superconductor with Rashba spin–orbit (SO) coupling[15] and the px + ipy topological superconductor[16] as examples to show the topological properties of the topological hierarchy superconductors. For both cases, there exist mid-gap energy bands induced by flux-superlattice and the mid-gap energy bands have nontrivial topological properties including the gapless edge states and non-zero winding number. Topological tight-binding Majorana lattice models are proposed to describe the mid-gap states.
The first example of topological hierarchy superconductor is an s-wave pairing SC with Rashba SO coupling and flux-superlattice.
The s-wave pairing SC with Rashba SO coupling on the square lattice is described by[18]

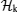
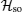


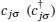
Firstly, we calculate the Majorana zero mode around a single vortex by the exact diagonalization numerical approach. According to the numerical results, there exists a localized state with exact zero energy around the vortex. The zero mode is localized around the vortex core within a length-scale ∼ m−1 (m is the mass gap). For this zero mode, the fermionic-quasiparticle operator satisfies 
Next, we numerically study the Majorana zero modes of a square flux-superlattice. The results are shown in Fig.
The density of state (DOS) of the TSC with a square flux-superlattice is shown in Fig.
To check the topological properties of the mid-gap system, we calculate its edge states. We consider a system on a cylinder with 12 super-unitcells along x-direction while periodic boundary along y-direction. The results are shown in Figs.
 | Fig. 2. (a) The illustration of vortex-lattice: the distance between two nearest vortices is 6a. The parameters are chosen as u = −4ts, λ = 0.5ts, h = 0.8ts, Δ = 0.5ts. Each vortex traps a Majorana mode. (b) The DOS of TSC with square vortex-lattice: the mid-gap states are induced by the vortex-lattice. The inset shows the details of the mid-gap energy band. (c) The spectrum flow of TSC with square vortex-lattice on a cylinder for the case of u = −4ts, h = 0.8ts, λ = 0.5ts, Δ = 0.5ts. There exist gapless edge states. (d) The spectrum flow of non-topological SC with square vortex-lattice on a cylinder for the case of u = −4ts, h = 0.8ts, λ = 0.5ts, Δ = 0.5ts. There exist no edge states. From Ref. [15]. |
Then, we propose an effective tight-binding lattice model of the s-wave TSC with a square flux-superlattice, in which each vortex traps a Majorana zero mode and two Majorana zero modes couple with each other by a short range interaction. We call this effective tight-binding lattice model as the Majorana lattice model, of which the effective Hamiltonian can be written as


To characterize the topological properties of the Majorana lattice model, we introduce the Chern number 


The second example of topological hierarchy superconductor is a topological px + ipy SC with flux-superlattice.
Topological px + ipy superconductivity is encoded in the following lattice Hamiltonian H (Fig.


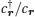
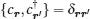
The topological properties of the topological px + ipy SC and those of the topological s-wave pairing SC with Rashba SO coupling are similar. If we do the unitary transformation

We then study the px + ipy topological SC with a flux-superlattice. We choose 8a × 4a sites to be a unit cell (8a along x-direction and 4a along y-direction), which indicates that the flux-superlattice is anisotropy. To show the topological properties of the mid-gap spectra, we put the system on a cylinder (open boundary condition along x-direction and periodic boundary condition along y-direction). The result of this case is plotted in Fig.
 | Fig. 3. (a) The illustration of topological px + ipy SC. (b) The energy splitting as a function of the space distance of two vortices. (c) The band structure of the topological superconductor with vortex superlattice on a cylindrical geometry. (d) The illustration of the gauge choice of the square Majorana lattice. Moving along the arrow, the fermion acquires a phase shift π/2. The accumulated phase encircling each triangular lattice plaquette anti-clockwise is −π/2. From Ref. [16]. |
Due to the unit cell of the vortex-superlattice is a rectangle, the effective tight-binding Majorana lattice model is given by


We obtain the tunneling parameters by fitting the energy dispersion of the mid-gap spectra induced by the flux-superlattice. As shown in the top panel of Fig. 4, the mid-gap spectra are obtained by a numerical approach.[23,24] The fitting dispersion of the effective tight-binding Majorana lattice model is shown in the bottom panel. We calculate the topological invariant of the effective tight-binding Majorana lattice model which gives the Chern number 
 | Fig. 4. Top panel: the contour plot of dispersion of mid-gap energy bands induced by vortex superlattice in px + ipy topological SC as a function of paired order parameter Δ in the zone kx⊗ky ∈ [−0.1,0.1]⊗[−0.2,0.2]. The paired order parameter is equal to 0.4, 0.8, 1.2, and 1.4 in panels (a), (c), (e), and (g), respectively. Bottom panel: the fitting dispersion of the effective tight-binding Majorana lattice model. From Ref. [16]. |
In the above section, we illustrate the s-wave pairing SC with Rashba SO coupling and the topological px + ipy SC with a square flux-superlattice. Due to the inter-vortex tunneling, there exist mid-gap energy bands induced by the flux-superlattice. We find that such mid-gap energy bands always have nontrivial topological properties including the gapless edge states and non-zero winding number. We can write down an effective tight-binding Majorana lattice model to characterize the mid-gap states and obtain the tunneling parameters by fitting the low energy spectrum with numerical calculations. Therefore, we call this type of topological superconductors with topological MG states topological hierarchy superconductors (THSC). In summary, a THSC is given by the following equation:

In this section, we review the topological hierarchy insulators.[13,30] We take the Haldane model as an example to show the topological properties. There are two types of topological hierarchy insulators: one type is induced by a flux-superlattice, and the other is induced by a vacancy-superlattice. The first type is similar to a topological superconductor with flux-superlattice, of which the mid-gap states are described by a Majorana lattice model and can be regarded as a “topological superconductor” on the parent topological superconductor.[15,16,25] For both cases, the overlap of different zero modes around the defects leads to mid-gap states inside the band gap of the parent TI. There exist mid-gap energy bands induced by defect-superlattices and the mid-gap energy bands have nontrivial topological properties including the gapless edge states and non-zero winding number. For both cases, we use an effective tight-binding model to characterize the mid-gap states induced by the superlattice of defects.
Based on the Haldane model on the honeycomb lattice, we review the topological hierarchy insulator from a topological insulator with a flux-superlattice.
The Hamiltonian of the Haldane model is given by[3]

By using the exact diagonalization numerical approach on a 72 × 72 lattice, we find that there exists a fermionic zero mode around each π-flux. The particle density is mainly localized around the π-flux. The length-scale of the wave-function of the zero mode is ξ ∼ vF/Δf, where vF = 3aT/2 is the Fermi velocity. When there are two fluxes nearby, the inter-flux quantum tunneling effect occurs and the two zero modes couple. The energy splitting δE between two energy levels versus the flux-distance L oscillates and decreases exponentially, which is shown in Fig.
 | Fig. 5. (a) The illustration of Haldane model on honeycomb lattice. (b) The energy splitting δE versus the flux-distance L for the case of T = 1.0, T′ = 0.1. a is the honeycomb lattice constant. The inset illustrates two π-flux with the flux-distance L. From Ref. [17]. |
Next we superpose a triangular flux-superlattice on the TI. By using the numerical calculations, we obtain the DOS for the Haldane model with a triangular flux-superlattice. See numerical results in Fig. 
To illustrate the topological properties of the mid-gap states induced by the flux-superlattice of the parent TI, we study the edge states of the TI with flux-superlattice for the case of T = 1.0, T′ = 0.1. We put the Haldane model with a finite flux-superlattice along x-direction on a torus. The parent topological insulator has the periodic boundary condition along both x-direction and y-direction. While the flux-superlattice has the periodic boundary condition along y-direction and the open boundary condition along x-direction. See the numerical results in Fig.
Finally, we also write down an effective tight-binding model to describe the mid-gap states. The quantum states of the fermionic zero mode around a π-flux can be formally described in terms of the fermion Fock states {|0⟩, |1⟩}. Here, |0⟩ and |1⟩ denote the unoccupied state and the occupied state, respectively. These quantum states are localized around the flux within a length-scale ξ ∼ vF/Δf. For the case of ξ < L, we can consider each flux as an isolated “atom” with localized electronic states and use the effective tight-binding model to describe these quantum states on the fluxes.
 | Fig. 6. (a) The DOS of TI with triangular flux-superlattice: the mid-gapped states are induced by the flux-superlattice with flux-superlattice constant  |
Now, we superpose the localized states to obtain the sets of Wannier wave functions w(R) with R denoting the position of the flux. Due to the formation of the triangular flux-superlattice, both the quantum-tunneling-strength δE between NN fluxes and the quantum-tunneling-strength δE′ between NNN fluxes exist. Owing to the inter-flux quantum tunneling effect, we obtain energy splitting |δERR′|, which is just the particle’s hopping amplitude |tRR′| between two localized states on two π-fluxes at R and R′. The effective tight-binding model of the two fermionic zero modes then takes the form of 


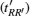
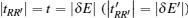
Now, we study the topological properties of the effective flux-superlattice model. According to the gauge shown in Fig. 7, we choose 

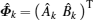
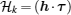

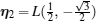


 | Fig. 7. The illustration of the gauge choice. Moving along the arrow (both blue arrow and red arrow), the fermion acquires a phase shift π/2. The accumulated phase encircling each triangular lattice plaquette anti-clockwise is π/2. From Ref. [17]. |
The topological quantum phase transition occurs when the band gap closes EVL(

 | Fig. 8. (a) The topological phases versus t′/t. (b) The density of states of the free flux-lattice model. The parameters are chosen as t/T = 0.04, t′/T = 0.014. (c) The edge states of the tight-binding model of flux-superlattice for the case of t′ = 0.1t, in which the Chern number is C = 1. (d) The edge states of the tight-binding model of flux-superlattice for the case of t′ = 3.1t, in which the Chern number is C = −3. From Ref. [17]. |
In Fig.
Hence, the low energy physics of the Haldane model with flux-superlattice can be described by an effective flux-superlattice model. The effective flux-superlattice model shows nontrivial topological properties, including a nontrivial topological invariant and gapless edge states. In this sense, the effective flux-superlattice model is really an emergent “topological insulator” on the parent TIs. Our results are more exotic than those in Ref. [32], in which a (non-topological) free-fermion model on a honeycomb lattice with flux-superlattice is studied.
We have studied the Haldane model with triangular flux-superlattice. Using a similar approach, we studied the Haldane model with other types of flux-superlattices such as the square flux-superlattice and honeycomb flux-superlattice, and found similar topological properties. In this sense, the topological mid-gap states always exist in a TI with flux-superlattice. In addition, we need to point out that the Kane–Mele model[5] or the spinful Haldane model[33] with flux-superlattice exhibit similar topological features. Due to the spin degree of freedom, a π-flux on these models traps two zero modes. The overlap of the zero modes also gives rise to a topological mid-gap system inside the band gap of the parent TIs. When one considers the interaction between the two-component fermions, the topological mid-gap system may lead to quite different physics consequences.
As a result, we call this type of topological insulators with topological MG states topological hierarchy insulators (THIs). In summary, THI from flux-superlattice is given by the following equation:

Based on the Haldane model on the square lattice, we review the topological hierarchy insulator from a topological insulator with a vacancy-superlattice.
The Hamiltonian of the (spinless) Haldane model on the square lattice is given by[3,34]

Vacancy is a non-topological defect and cannot induce a fermion zero mode when we consider a vacancy in TI. However, we have pointed out that if the Hamiltonian has the particle–hole (PH) symmetry, then a vacancy can induce a zero mode. Under PH transformation, we have

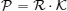
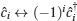
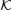
 | Fig. 9. (a) The illustration of the Haldane model on square lattice. Blue and red dots represent A,B sublattices. The blue arrows represent t′ and the dashed blue arrows represent −t′. (b) The particle density distribution around the zero energy vacancy. (c) The energy splitting ΔE between two vacancies as a function of L (the distance of two nearby vacancies). The parameter is t′ = 0.2t. From Ref. [30]. |
The Hamiltonian in Eq. (
We next study the Haldane model with vacancy-superlattice. When there are two vacancies nearby, the inter-vacancy quantum tunneling effect occurs and the fermionic zero modes on the two vacancies couple. The lattice constant of the vacancy-superlattice (VSL) is denoted by L, which is the distance between two nearby vacancies. When the vacancies are located on different sublattices, the energy splitting ΔE is finite (L/a is an odd number); when the vacancies are located on the same sublattice, the energy splitting vanishes, ΔE = 0 (L/a is an even number). The energy splitting ΔE between two vacancies as a function of L is shown in Fig.
For the case of ξ < L, we can consider each vacancy as an isolated “atom” with localized electronic states and use the effective tight-binding model to describe these quantum states induced by the VSL. We now construct the superpositions of the localized states to obtain the sets of Wannier wave functions ψ0(ri − R). In general, the effective tight-binding model of the localized states induced by the VSL becomes

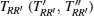
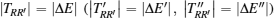


Because the energy splitting ΔE only determines the particle’s hopping amplitude |tRR′|, we need to settle down the phase of TRR′. In particular, to preserve the PH symmetry, the total phase around a plaquette with four NN vacancies can be either π or 0. One approach is to count the total flux number inside the plaquette. For the mid-gap states induced by VSL, every four NN vacancies form an L × L square, of which the total flux number is just L2/2 and the total phase around a plaquette is πL2. After considering the compact condition, we have 0/π-flux inside each plaquette if L2 is an even/odd number. In addition, we also use a numerical approach to check the above prediction of the flux number inside the plaquette.
We then consider the Haldane model with a square-VSL and the lattice constant L set to 3a. See the illustration in Fig.
 | Fig. 10. (a) The illustration of square-VSLs on square lattice. (b) The DOS of the Haldane model with square-VSL for L = 3a: the mid-gap states are induced by the square-VSL. (c) The edge states of mid-gap states. The parameter is t′/t = 0.2. (d) The DOS of TFI. The insets show the DOSs of the mid-gap states. From Ref. [30]. |
As a result, we obtain an effective Hamiltonian that describes the vacancy-induced square lattice, written in the form

From the DOS of the Haldane model with square-VSL for t′/t = 0.2 and L = 3a in Fig.
To illustrate the topological properties of the Haldane model with square-VSL, we study its edge states. As a result, when the system has periodic boundary condition along y-direction but open boundary condition along x-direction, there exist the gapless edge states. On the other hand, we consider the half filling case, of which the system has zero Chern number. When the parent topological insulator has periodic boundary condition along both x-direction and y-direction, while the VSL has periodic boundary condition along y-direction but open boundary condition along x-direction, there may exist gapless edge states. See the numerical results in Fig.
In addition, we also calculate the Haldane model on the honeycomb lattice with the honeycomb-VSL. The Haldane model on the honeycomb lattice also has the PH symmetry, and honeycomb-VSL can also induce a topological hierarchy insulator.
In general, the Haldane model with a square-VSL of odd number L2 has nontrivial topological properties and is different from the traditional TIs. As a result, we call this type of topological insulator with topological MG states topological hierarchy insulators (THIs). In summary, THI from vacancy-superlattice is given by the following equation:

There also exist a particular type of topological hierarchy insulator, topological fractal insulator (TFI), which is a topological hierarchy insulator with infinite generations of self-similar L × L-square-VSLs. To construct a TFI, we first consider a topological hierarchy insulator with self-similar MG states. Because we can tune t′/t (or ΔE′/ΔE) by changing the NNN hopping parameter t′ of the parent TI or the VSL constant L, the MG states can be self-similar to the parent topological states for the case of T/T′ = t/t′. From numerical calculations, we obtain the self-similarity case, where smaller/bigger t/t′ leads to bigger/smaller T/T′. Now, under the self-similar condition T/T′ = t/t′, the effective Hamiltonian that describes the MG states becomes

Next, we regard the vacancy-induced MG states as a parent TI and introduce an additional VSL on it. Using the recursive relation, we can see that there exist additional MG states inside the energy gap of the first generation MG states (which we refer to as generation-1 MG states). Consequently, we obtain a new generation of topological MG states (we call such MG states in the energy gap of the MG states as generation-2 MG states). Using the same procedure, we can construct a THI with n-generation MG states and eventually a THI with infinite generations of self-similar MG states that is just a TFI. Then, under the self-similar condition T/T′ = t/t′, the effective Hamiltonian of the generation-n MG states is given by

It is known that a self-similar object looks “roughly” the same on different scales and fractal is a particularly self-similar object that exhibits a repeating pattern displaying at every scale. The topological fractal insulator provides a unique example of topological matters with self-similarity, in which the topological properties always look the same on different energy scales (α2n) or different length scales (L2n).
In this review, we mainly talk about the defects induced topological states in TIs/TSCs. A new type of topological matter is defined — topological hierarchy matter. There are two types of topological hierarchy matters: one is the topological hierarchy superconductor induced by flux-superlattice, and the other is the topological hierarchy insulator induced by vacancy-superlattice or flux-superlattice. After considering the superlattice of defects, the topological mid-gap states are induced in these topological hierarchy matters. The topological mid-gap states may have nontrivial topological properties, including the nonzero Chern number and the gapless edge states. Effective tight-binding models are obtained to describe the topological mid-gap states in the topological hierarchy matters.
In the future, an important issue is to look for the topological hierarchy superconductor induced by vacancy-superlattice. For the topological hierarchy insulator, the correlation effect may be more relevant than that in the traditional correlated topological insulator. So, we will study the correlated hierarchy topological insulator and find new type quantum exotic states after considering the correlation effect. Furthermore, we try to realize topological hierarchy matters in condensed matter physics and explore their non-trivial topological properties. On the other hand, cold atoms in optical lattices are an extensively developing research field.[37–40] By using the ultracold-atom technique, we can accurately control the interaction. The cold atoms in optical lattices are an ideal experimental platform for realizing topological hierarchy matters.



