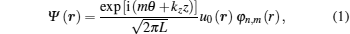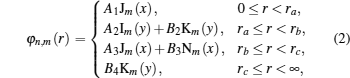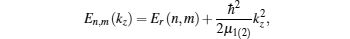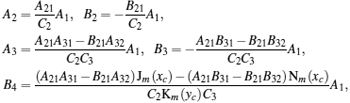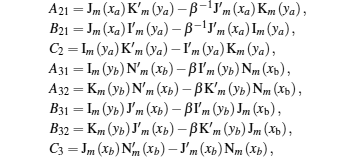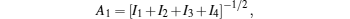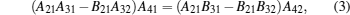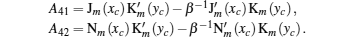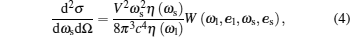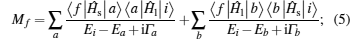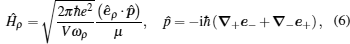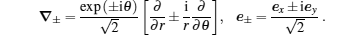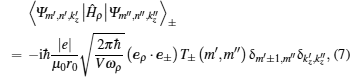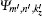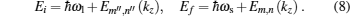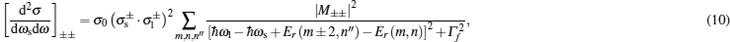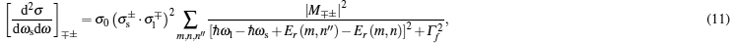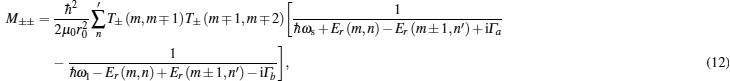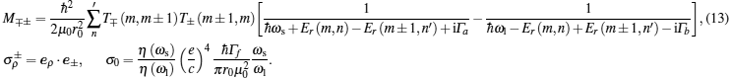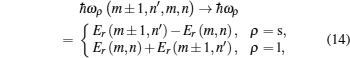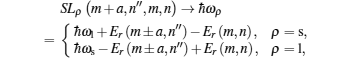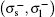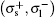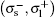2. Model and electronic statesWe must determine the stationary states of an electron in a double quantum well wire system of cylindrical geometry, where ra, rb, and rc are the radii and length L. The confinement potential (Vc) and the effective mass (μ) are given by

The envelope function approximation leads to the solution of Schrödinger equation
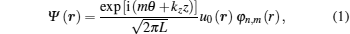
where
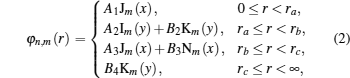
where
u0 (
r) is the electron Bloch function in the band; J
m and N
m are the Bessel functions of the first and the second kind of order
m; I
m and K
m are the modified Bessel functions of the first and the second kind of order
m. Here, we use the definitions of Bessel functions according to Abramowitz.
[30] The electron energy is given by
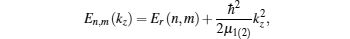
where

where
Er is the energy due to the spatial confinement. By considering the continuity of the function
Ψ and the current density (1/
μ)(
∂Ψ/
∂r) at the interface, we can calculate the constants
A and
B present in Eq. (
2); also can determine energy levels
Er, then
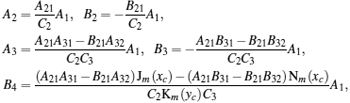
with
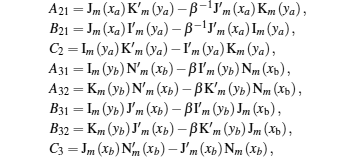
being
xk =
x (
rk) and
yk =
y (
rk),
A1 can be obtained using the normalization condition, therefore,
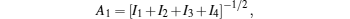
where

In addition, Er is determined from the following transcendental equation:
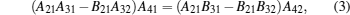
where
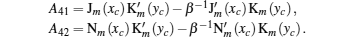
As it can be observed, for each value of
m,
n energy values are obtained. The states are then described by the following quantum numbers:
m = 0,1,2,…;
n = 1,2,3,…; and
kz (see Ref. [
27]). We can say that the system is the combination of a quantum well wire of cylindrical disk geometry in the region where
r ≤
ra, which we call “the wire”, and a quantum well wire with a cylindrical ring geometry in the region where
rb ≤
r ≤
rc, which we call “the shell”; while the barrier is the region where
ra <
r <
rb.
3. Raman cross-sectionThe Raman differential cross-section in a volume per unit solid angle for incoming light of frequency ωl and scattered light of frequency ωs is given in Ref. [12], and it can be written as
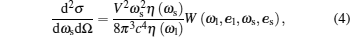
where
η(
ωρ) is the refraction index as a function of the radiation with frequency
ωρ and polarization unit vector is
eρ. The subindex
ρ =
l(
s) indicates the incident (secondary) radiation;
c is the light velocity in a vacuum,
V is the volume, and
W(
ωl,
el,
ωs,
es) is the transition rate for the absorption and emission radiation calculated according to Fermi’s golden rule. In this case, two possibilities must be considered: (i) the electron absorbs the incident photon and it later emits the secondary radiation photon; or (ii) the electron emits the secondary radiation photon and later absorbs the incident photon.
[28] Therefore,

where
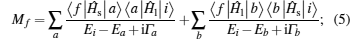
in which |
i⟩ and |
f⟩ are the initial and final states with energies
Ei and
Ef, respectively; |
a⟩ and |
b⟩ are the intermediate states with energies
Ea and
Eb, respectively; and finally
Γa and
Γb are their respective lifetimes.
[1]The Hamiltonian operator for the radiation field Ĥρ, with frequency ωρ and polarization unit vector eρ, is commonly used in electron Raman scattering and resonant Raman scattering in nanostructures in the dipole approximation. This approximation is valid as long as the radiation wavelength is much larger than the radius of the wire. The effect of reduced dimensionality on the free carrier absorption and the selection rules for intersubband transition have been discussed in Ref. [28], where it is shown that the electron Raman scattering can only take place in the confinement direction, then
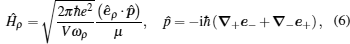
with
μ the electron effective mass, and
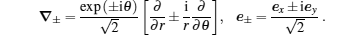
Now, we must calculate the matrix elements appearing in Eq. (5). We use the condition k = 0 for the radiation field;[28] thus, by considering Eqs. (1) and (6), the following matrix elements can be obtained:
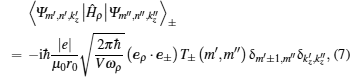
where
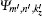
and
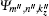
are the final and initial states of the transition, respectively, and

and
μ0 is the electron free mass.
The explicit forms of Im′m″ and IIm′m″ are very complicated and their expressions can be calculated following the method reported in Ref. [31]. As it can be observed, the emission or absorption of one photon can only take place between consecutive states of the quantum number m, according to the selection rules m″ = m′ ± 1, although there is no restriction for the quantum number n (see Eq. (7)).
In the initial state, we have an electron in a conduction subband and an incident radiation photon; and for the final state, we have an electron in the other conduction subband and a secondary radiation photon
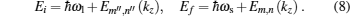
For the intermediate states

Using Eqs. (7)–(9), we can obtain four different contributions to the differential cross section (see Ref. [27]), depending on the polarizations of the incident and emitted radiation, and finally we can rewrite Eq. (4) as

where
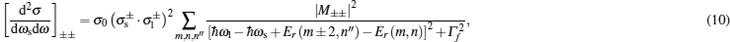
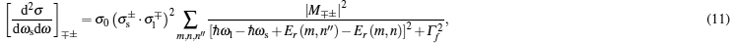
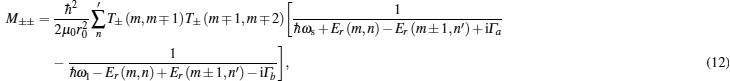
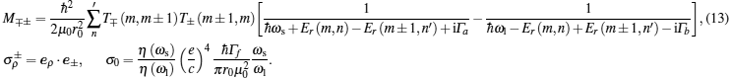
4. Discussion of the obtained resultsIn this case, we considered a cylindrical semiconductor double quantum wire grown in a GaAs/Al0.35Ga0.65 As matrix, and the following physical parameters[29] were used in this calculations: μ1 = 0.096μ0, μ2 = 0.0665μ0, and V0 = 0.30 eV, where μ0 is the free electron mass. Furthermore, in all cases, it is considered that Γa = Γb = Γf = 1 meV.
Figure 1 shows the electron state energy, Er of the double quantum well wire (solid lines), obtained using Eq. (3); where the values of ra and rc are fixed and rb takes values in the range of (ra, rc). In Figs. 1(a)–1(c), ra = 6.0 nm and rc = 12.0 nm, ra = 6.0 nm and rc = 14.0 nm, ra = 8.0 nm and rc = 14.0 nm, respectively. The dashed lines correspond to the energies of a simple quantum well wire with radius ra. In this type of system, we can say that levels belong mainly to the wire or to the shell, but we must take into account that the quantum states actually belong to both, i.e., belong to the system; this is what we refer to as “coupling”.[32,33] Initially, in Fig. 1, we have a simple quantum well wire with radius rc, because rb = ra. As rb increases, the double quantum well wire is formed; such that the width of the shell, d = rc − rb, diminishes and increases the width of the barrier, b = rb − ra. Finally, when rb = rc, we obtain a simple quantum well wire with radius ra. In Fig. 1(a), we can see that the electron state denoted by m = 0 and n = 1 is the ground state of the system, and is contained primarily in the wire, as it tends to a simple quantum well wire when the radius rb increases.[32] Besides, using the same argument we can determine that the electron state denoted by m = 0 and n = 2 is contained primarily in the shell, being the electron state of the shell with the lowest energy; but this is only true in the region rb > 6.6 nm; so this is the point where the system coupling begins to break. We can say that for 0 < rb < 6.6 nm, the system is in strong coupling. It can be observed that for rb ≈ 8.0 nm, the electron states corresponding to a shell are “taken out” from the system, due to the increase of the confinement of the electrons in this region. Moreover, we can see that the level denoted by m = 0 and n = 1 reaches the energy of a simple quantum well wire when rb ≈ 10.0 nm.
If we compare Fig. 1(b) with Fig. 1(a), the rc value is increased, rc = 14.0 nm, being the immediate consequence of the increase in the number of electronic states “within” the system. Again, we have only one level of the wire, m = 0 and n = 1, which is logical as it remains the same value of ra = 6.0 nm, and again this is the lowest energy level. We can see that the electron state labeled as m = 0 and n = 2, cuts the level of the shell with the electron state, m = 1 and n = 1, approximately in rb = 8.0 nm, which determines the range where the coupling is strong. In this case, the strong coupling is in the range from b = 0 to b = 2.0 nm; that is larger than that obtained in Fig. 1(a). This implies that the increase of rc increases the size of the strong coupling region. Also, it is observed that the electronic states primarily associated with the shell, are organized in subbands determined by the quantum number n, see Fig. 1 of the Ref. [27]. In addition, we see that the electron state, which is denoted by m = 0 and n = 1, and associated mainly with the wire, reaches the energy of a simple quantum well wire when rb ≈ 10.0 nm. Comparing Fig. 1(a) with Fig. 1(b), we can conclude that increasing rc enlarges the strong coupling region, but practically does not change the point where the electron state denoted by m = 0 and n = 1 reaches the energy of a simple quantum well wire.
Moreover, in Fig. 1(c), the radii are set as ra = 8.0 nm and rc = 14.0 nm, which means that the radius of the wire is greater than that in Fig. 1(b) while the value of rc is the same. Comparing these two figures, we can find that the coupling increases because the barrier becomes smaller. Moreover, we can see that with the increase of the radius of the wire, the number of states that “fit” inside also increases, so there are primarily two energy levels associated with the wire. In these electron states mainly related to the wire, it is shown that the higher the energy is, the higher the coupling is, because the “barrier height” that must be overcome by the electrons is lower. When comparing these three figures in Fig. 1, we can see that the states with different values of m can be cut, while if it has the same value of m, it is not possible.
Figure 2 shows the energy of electron states, Er, for the double quantum well wire (black solid lines), where the barrier varies while the width of the shell is fixed, and the radii of the wire are ra = 6.0 nm and d = 6.0 nm, ra = 6.0 nm and d = 8.0 nm, and ra = 8.0 nm and d = 6.0 nm in Figs. 2(a)–2(c), respectively. The dashed red lines correspond to the quantum state of a quantum well wire of cylindrical ring geometry with width d, while dashed blue lines correspond to the quantum state of a quantum well wire of cylindrical geometry with radius ra. In Figs. 2(a)–2(c), we can see that all the electron states are corresponding with the band given by n = 1, as can be observed in Fig. 2 of Ref. [27]. Furthermore, in the three cases shown in Fig. 2, initially, the barrier does not exist, b = 0; this means that initially it has a simple quantum well wire with radius rc. By comparing Figs. 2(a)–2(c), it can be deduced that the levels associated mainly to the wire do not cut each other, the same situation occurs with levels associated primarily to the shell, if they can cut the levels associated to different system components. In Fig. 2(a), it can be seen that as the barrier increases, the energy levels are adjusted to the energy levels corresponding to a shell (dashed red lines) and to a wire (dashed blue lines). For values of the barrier about 4.0 nm, we cannot find virtually any difference between the levels corresponding to the double quantum well wire and corresponding to the shell and to the wire, for any energy level. If we observe the levels associated with the shell, we can conclude that for higher energy, the decoupling is faster, because the “barrier height” that must be overcome by the electrons is lower. In the case, when electron states are associated primarily to the wire, the value of the barrier required for decoupling is approximately b = 1.5 nm, which is lower than that for the shell, so we can say that for the wire the decoupling is faster.
In Fig. 2(b), we increase the width of the shell at d = 8.0 nm, while maintaining the same internal radius, ra = 6.0 nm; this causes an increase in the number of levels mainly associated with the shell that are “within” the system, while it remains the number of associated states primarily to the wire. Comparing Fig. 2(b) with Fig. 2(a), we can see that the energy levels of double quantum wire are made virtually equal to the levels of the shell, from a width of about b = 2.5 nm. This means that when the width of the shell is increased, the electron states associated mainly to the shell are decoupled faster; so we can conclude that the coupling is weakened for the states of the shell. However, if we observe the blue dashed lines, it is noted that for the electron states associated primarily to the cable the decoupling requires a higher value of the barrier; in this case approximately b = 5.0 nm. Hence, we can conclude that in the case of states of the wire, the increase of d reinforces the coupling. Moreover, in Fig. 2(c) unlike in Fig. 2(a), we increase the value of ra to 8.0 nm, and the width of the shell, d = 6.0 nm remains constant. First, we note that two levels associated with the wire (dashed lines) appear, this is because if the radius is greater, more levels “within” the system can be found. Furthermore, it can be seen that the decoupling of the energy levels associated with the shell occurs to a value similar to the one seen in Fig. 2(a). On the other hand, in the case of the states associated to the wire, we can observe a coupling increase. Therefore, the coupling of the energy levels associated with the shell depends mostly on the width rather than the radius of the wire; while in the case of electron states associated with the wire, the coupling depends on the width and the radius of the shell and the wire, respectively.
Now, we have to analyze the differential cross section of the electron Raman scattering, which can explain the singularities presented in the emission and excitation spectra, respectively. In this case, we must note that equations (12) and (13) have resonant singularities, which are independent of the incident photon, or of the secondary photon when
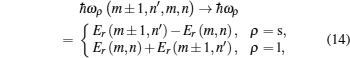
where
ρ = s is for the emission spectrum and
ρ = l is for the excitation spectrum. While for Eqs. (
10) and (
11), we have the non-resonant singularities, which are dependent on the incident photon or the secondary photon for the emission spectrum and for the excitation spectrum, respectively, then
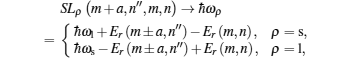
where
a = 2 for

and
polarizations, and
a = 0 for
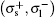
and
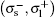
polarizations. If the energy of the incident radiation is different to the resonance, this difference is named detuning.
Figure 3 shows the emission spectrum of a double quantum well wire with ra = 9.0 nm, rb = 12.0 nm, and rc = 17.0 nm, for incident photon with energy ħωl = 0.28 eV, where:  (Fig. 3(a)),
(Fig. 3(a)),  (Fig. 3(b)),
(Fig. 3(b)),  (Fig. 3(c)). If we compare the contribution
(Fig. 3(c)). If we compare the contribution  (Fig. 3(a)) with the contribution
(Fig. 3(a)) with the contribution  (Fig. 3(b)), we can see that the intensity of the resonant singularities is smaller, moreover it can also be noted that the position of singularities change. This is because the two figures correspond to two different polarizations of secondary radiation,
(Fig. 3(b)), we can see that the intensity of the resonant singularities is smaller, moreover it can also be noted that the position of singularities change. This is because the two figures correspond to two different polarizations of secondary radiation,  , which affects the selection rules of m ± 1 = m′. As we can see, the position of singularities in the graph is related to the “gap” between the two energy levels involved, while the peak intensity is mainly related to the probability of the transition and the detuning (see Ref. [29]), if the incident radiation (ħωl) is the same. When comparing Fig. 2(c) with Figs. 2(a) and 2(b), it is easy to see that the intensity of the resonant singularity is higher by almost an order of magnitude, that being the reason for the main contribution to the differential cross section. Also, we can see that the resonant singularities in polarizations
, which affects the selection rules of m ± 1 = m′. As we can see, the position of singularities in the graph is related to the “gap” between the two energy levels involved, while the peak intensity is mainly related to the probability of the transition and the detuning (see Ref. [29]), if the incident radiation (ħωl) is the same. When comparing Fig. 2(c) with Figs. 2(a) and 2(b), it is easy to see that the intensity of the resonant singularity is higher by almost an order of magnitude, that being the reason for the main contribution to the differential cross section. Also, we can see that the resonant singularities in polarizations  and
and  are the same, this is because the secondary radiation fulfills in both cases the identical selection rule.
are the same, this is because the secondary radiation fulfills in both cases the identical selection rule.
Moreover, figure 4 shows the emission spectrum for an electron Raman scattering process in double quantum well wire for incident photon energy ħωl = 0.28 eV and polarization  . In Fig. 4(a), the dashed line corresponds to ra = 8.0 nm, rb = 10.0 nm, and rc = 15.0 nm, while the solid line corresponds to ra = 9.0 nm, rb = 10.0 nm, and rc = 15.0 nm. In Fig. 4(a), the dashed line corresponds to ra = 8.0 nm, rb = 10.0 nm, and rc = 16.0 nm, while the solid line corresponds to ra = 8.0 nm, rb = 12.0 nm, and rc = 17.0 nm. In Fig. 4(b), the dashed line has been multiplied by 10. As it can be seen in Fig. 4(a) that the increase of the radius of the wire, ra, causes an increase in the number of singularities and position changing of singularities, which we can already see in the spectrum, and these singularities move to a lower energy position. This is because the increase of ra increases the number of quantum states “within” the system, especially those mainly related to the wire, while the gap between different subbands decreases (see Eq. (14)). This is corroborated if we observe the resonant singularity denoted by ħωs (1,1,0,1) in both figures. In addition, in Fig. 4(b), we maintain a constant radius of the wire, ra = 8.0 nm, and change the width of the shell and the barrier. However, the position of the singularity ħωs(1,1,0,1), remains constant (also, note the dashed line in Fig. 4(a); this confirms that the quantum states m = 1, n = 1 and m = 1, n = 1 belong mainly to the wire. If we look at the singularity ħωs (1,2,0,1), this moves to a position of greater energy, which is because the quantum state labeled as m = 1, n = 2, is mainly related to the shell. Furthermore, we can compare the dashed line in Fig. 4(a) with the dashed line in Fig. 4(b). In this case, the width of the shell is increased by rc, increasing and it causes a similar effect to the one described in Fig. 4(a), but mainly affecting quantum states of the shell, allowing the occurrence of singularities related to the ones with the energy levels of the shell. Whereby, we clarify that the increase of ra mainly affects the energy levels belonging to the wire, while the increase of rc primarily affects the energy levels belonging to the shell. Finally, the dashed line in Fig. 4(a) and the solid line in Fig. 4(b) can be compared. We can see that the increment of the barrier, b, keeping a constant width, d, only causes a small change in the position of the resonant peak, which corresponds with that observed in Fig. 2, but affects the intensity of the singularities.
. In Fig. 4(a), the dashed line corresponds to ra = 8.0 nm, rb = 10.0 nm, and rc = 15.0 nm, while the solid line corresponds to ra = 9.0 nm, rb = 10.0 nm, and rc = 15.0 nm. In Fig. 4(a), the dashed line corresponds to ra = 8.0 nm, rb = 10.0 nm, and rc = 16.0 nm, while the solid line corresponds to ra = 8.0 nm, rb = 12.0 nm, and rc = 17.0 nm. In Fig. 4(b), the dashed line has been multiplied by 10. As it can be seen in Fig. 4(a) that the increase of the radius of the wire, ra, causes an increase in the number of singularities and position changing of singularities, which we can already see in the spectrum, and these singularities move to a lower energy position. This is because the increase of ra increases the number of quantum states “within” the system, especially those mainly related to the wire, while the gap between different subbands decreases (see Eq. (14)). This is corroborated if we observe the resonant singularity denoted by ħωs (1,1,0,1) in both figures. In addition, in Fig. 4(b), we maintain a constant radius of the wire, ra = 8.0 nm, and change the width of the shell and the barrier. However, the position of the singularity ħωs(1,1,0,1), remains constant (also, note the dashed line in Fig. 4(a); this confirms that the quantum states m = 1, n = 1 and m = 1, n = 1 belong mainly to the wire. If we look at the singularity ħωs (1,2,0,1), this moves to a position of greater energy, which is because the quantum state labeled as m = 1, n = 2, is mainly related to the shell. Furthermore, we can compare the dashed line in Fig. 4(a) with the dashed line in Fig. 4(b). In this case, the width of the shell is increased by rc, increasing and it causes a similar effect to the one described in Fig. 4(a), but mainly affecting quantum states of the shell, allowing the occurrence of singularities related to the ones with the energy levels of the shell. Whereby, we clarify that the increase of ra mainly affects the energy levels belonging to the wire, while the increase of rc primarily affects the energy levels belonging to the shell. Finally, the dashed line in Fig. 4(a) and the solid line in Fig. 4(b) can be compared. We can see that the increment of the barrier, b, keeping a constant width, d, only causes a small change in the position of the resonant peak, which corresponds with that observed in Fig. 2, but affects the intensity of the singularities.
The change in the intensity of differential cross section for an electron Raman scattering process in semiconductor double quantum well wire is related to the coupling between the wire and the shell. This is evidently shown in Fig. 5, in which a transition rate that describes the following process is shown: first, an electron in the conduction band absorbs a photon of incident radiation, resulting in a transition from initial state m″ = 0, n″ = 1 to intermediate state m′ = 1, n′ = 1; then, the electron emits a photon of secondary radiation due to a new transition, from intermediate state m′ = 1, n′ = 1 to final state m = 0, n = 2. It is important to note that the net Raman gain in this case is directly proportional to the transition rate, this is |T− (0,1)T+ (1,0)|2. Then, figure 5 shows the rate transition to a wire for a double quantum well, where the barrier b varies while the fixed values of ra and d remain. In addition, we must note that the solid line corresponds to a double quantum well where ra = 8.0 nm and d = 6.0 nm, being the dash line the one that corresponds to a double quantum well where ra = 8.0 nm and d = 8.0 nm. These curves are much like those obtained from an asymmetric multiple quantum well[32] and different from those obtained for a step-quantum well;[29] this is because the double quantum well wire can be decoupled as the asymmetric multiple quantum well, but in the present case the coupling is weakened much faster. Summarizing, the coupling in a double quantum well wire with cylindrical symmetry is weaker than an asymmetrical double quantum well. In addition, it is noted that any change in the system parameters causes strong changes in the transition rate, making this system very difficult to optimize. However, although the coupling is weak in this system, the transition rate is larger than the one obtained for the asymmetrical double quantum well, observed in Fig. 6 in Ref. [32], which is due to the symmetry of the system. We should clarify that when we refer to the coupling, we are referring to the interaction between the parts of the active region of the system, which in this case are the wire and the shell. This interaction affects the electronic states of the system, so that the electronic states are a mix between wire electron states and shell electron states.