Project supported by the National Key R & D Program, China (Grant No. 2016YFA0301700), the Research Grant Council, University Grants Committee, Hong Kong, China (Grant No. 17303714), the National Natural Science Foundation of China (Grant No. 11574127), and the National Thousand-Young-Talents Program of China.
Weak localization and antilocalization are quantum transport phenomena that arise from the quantum interference in disordered metals. At low temperatures, they can give distinct temperature and magnetic field dependences in conductivity, allowing the symmetry of the system to be explored. In the past few years, they have also been observed in newly emergent topological materials, including topological insulators and topological semimetals. In contrast from the conventional electrons, in these new materials the quasiparticles are described as Dirac or Weyl fermions. In this article, we review our recent efforts on the theories of weak antilocalization and interaction-induced localization for Dirac and Weyl fermions in topological insulators and topological semimetals.
Weak antilocalization is a transport phenomenon in the quantum diffusion regime in disordered metals.[1] The quantum diffusion in disordered metals can be defined by the mean free path ℓ and the phase coherence length ℓϕ. The mean free path measures the average distance that an electron travels before its momentum is changed by elastic scattering from static scattering centers, while the phase coherence length measures the average distance that an electron can maintain its phase coherence. If the mean free path is much shorter than the system size and the phase coherence length, then the electrons suffer from scattering but can maintain their phase coherence. This is the quantum diffusive regime, in which the quantum interference between time-reversed scattering loops (see Fig.
The phase coherence length is determined by inelastic scattering from electron–phonon coupling and interaction with other electrons. The inelastic scattering has to be suppressed significantly to make the phase coherence length much longer than the mean free path. Therefore, the quantum diffusion usually takes place at extremely low temperatures; e.g., below the liquid helium temperature. If the quantum interference correction is positive, then it gives a weak antilocalization correction to the conductivity and the conductivity goes up with decreasing temperature (see Fig.
In contrast, the quantum interference can be negative, leading to a weak localization effect and totally opposite temperate and magnetic dependencies of conductivity. Whether a system has weak localization or weak antilocalization depends on the symmetry (see Table
| Table 1. The relation between the symmetry classes (orthogonal, symplectic, and unitary)[2] and the weak localization (WL) and antilocalization (WAL).[3] . |
In the last decade, weak antilocalization has been widely observed in topological materials, such as topological insulators[4–9] and topological semimetals,[10–13] in which the quasiparticles are described not by the Schrödinger equation but as Dirac fermions in the topological insulators and Weyl fermions in the topological semimetals. For Dirac fermions, the weak antilocalization has an alternative understanding based on the Berry phase argument. The Berry phase is a geometric phase collected in an adiabatic cyclic process.[14,15] Since studies on carbon nanotubes have begun, it has been found that massless Dirac fermions can collect a π Berry phase after circulating around the Fermi surface.[16] The π Berry phase induces a destructive quantum interference between time-reversed loops formed by scattering trajectories. The destructive interference can suppress backscattering of electrons, the conductivity is then enhanced with decreasing temperature because the decoherence mechanisms are suppressed at low temperatures.[17,18]
One of the powerful theoretical approaches to study weak localization and antilocalization is the Feynman diagram techniques. Figure
In this paper, we review our recent efforts[19–22] on the weak antilocalization and interaction-induced localization of Dirac and Weyl fermions in topological insulators and topological semimetals.[19–25] Part of the contents have been reviewed in Ref. [26], where only topological insulators are addressed. In Section 2, we discuss the Berry phase argument and the crossover between weak antilocalization and weak localization in magnetically modulated topological insulator and topological insulator thin films. In Section 3, we show the weak localization of Dirac fermions as a result of electron–electron interactions. In Section 4, we review the weak antilocalization and interaction-induced localization of Weyl fermions in 3D topological semimetals. Finally, remarks and perspective are given in Section 5.
 | Fig. 2. (a) The diagrams for the semiclassical conductivity σsc. v and  |
Topological insulators are gapped band insulators with topologically protected gapless modes surrounding their boundaries.[4–9] The surface of a three-dimensional topological insulator hosts an odd number of two-dimensional gapless Dirac cones. The Dirac cone has a helical spin structure in momentum space.[27] The topological insulators have attracted tremendous interest in their transport properties.[28,29] It turns out that the known topological insulator materials all have poor mobility. The mean free path is of the order of 10 nm, while the phase coherence length can reach up to 100–1000 nm below the liquid helium temperature. In other words, these materials are well in the quantum diffusion regime at low temperatures, where the weak (anti-)localization is expected. In experiments, the negative magnetoconductivity arising from the weak antilocalization has been observed in almost every topological insulator sample.[30–39]
The surface states of a topological insulator can be described by a two-dimensional massless Dirac model


The Berry phase is a geometric phase collected in an adiabatic cyclic process,[15,16] and it can be found as

The π Berry phase can give an explanation of the weak antilocalization of the two-dimensional massless Dirac fermions. The time-reversed scattering loops in Fig.
To verify the role played by the Berry phase, one can alter the Berry phase by including a mass to the Dirac model[7,44]

Now the conduction and valence bands are separated by a gap Δ. With the mass term, the Berry phase turns out to be[20]

An alternative definition of a topological insulator is that its topologically protected surface states cannot be localized.[4,5,42,43] The negative magnetoconductivity of the weak antilocalization has been regarded as a signature of this delocalization tendency. However, in most experiments, a suppression of the conductivity with decreasing temperature is observed (see Fig.
The electron–electron interaction[64,65] provides a possible way to understand the contradictory magnetic field and temperature dependences.[19] The interplay of the interaction and disorder can lead to a temperature dependence much like the weak localization, known as the Altshulter–Aronov effect.[64,65] The theory is established for conventional electrons. We show that Dirac fermions are not immune from the Altshuler–Aronov effect. With or without the magnetic field, the correction from the interaction to the conductivity decreases logarithmically with decreasing temperature. Although the weak antilocalization can enhance the conductivity with decreasing temperature, it is overwhelmed by the contribution from the interaction effect. Therefore, the overall temperature dependence of the conductivity shows a weak localization tendency. Our theoretical results agree well with the experiments, with comparable changes of the conductivity (several e2/h), temperatures (0.1 to 10 K), and magnetic fields (0 to 5 T).[35–37,60–62]
 | Fig. 3. (a) Measured logarithmic temperature-dependent conductivity (solid lines) at zero magnetic field for all samples with the edge-to-edge distance between antidots d indicated. The red dashed lines are guide for eyes. (b) Measured logarithmic temperature-dependent conductivity at indicating perpendicular magnetic fields (open circles) for sample d190. Solid lines are the linear fitting curves. (c) Measured temperature-dependent conductivity (solid lines) at B = 2 T for all samples with d indicated. The curves are offset for clarity and the red dashed lines are guide for eyes. (d) The slope obtained by linear fitting the curves in panel (b) is plotted (solid symbols) as a function of the magnetic field for sample d190. Solid lines are guide for eyes. Adapted from Ref. [59]. |
Furthermore, to verify the interaction effect, we proposed an artificial nanostructure[59] as shown in Fig.

In strong magnetic fields, the slope is solely determined by the interaction effect. As an interaction effect, the slope is supposed to be changed by changing the dielectric constant ɛr. We calculated the slope from the interaction κee as a function of ɛr for the surface electrons as plotted in Fig.
To modulate the dielectric constant, we fabricated an array of antidots arranged in a periodic triangular lattice in thin films of Bi2Te3, as schematically indicated in Fig.
In this way, we show that two-dimensional massless Dirac fermions can show the localization tendency when both the electron–electron interaction and disorder scattering are taken into account.
 | Fig. 4. (a) Schematic illustration of a Hall bar sample with antidot array. (b) Scanning electron microscopy image of a Bi2Te3 thin film with antidot array, where the edge-to-edge distance between antidots d = 40 nm. The inset is the atomic force microscope image indicating that the antidots depth is about 25 nm. Adapted from Ref. [59]. |
 | Fig. 5. (a) The calculated slope κee as a function of relative dielectric constant ɛr for gapless Dirac fermions. vħ is chosen to be 2.5 eV·Å, comparable with that in the experiment.[66] (b) The slope κ of the conductivity–ln T curve as a function of magnetic field B for different antidot distance d. The measured κ (scatters) are fitted by the theory[19] (solid curves). (c) The dielectric constant as a function of d, obtained by fitting the transport theory (ɛr) and calculated from the Bruggeman effective medium theory  |
Weyl semimetal is a three-dimensional (3D) topological state of matter, in which the conduction and valence energy bands touch at a finite number of nodes.[10] The nodes always appear in pairs, in each pair the quasiparticles (dubbed Weyl fermions) carry opposite chirality and linear dispersion, much like a 3D analog of graphene. In the past few years, a number of condensed matter systems have been suggested to host Weyl fermions.[11–13,70–78] Recently, angle-resolved photoemission spectroscopy (ARPES) has identified the Dirac nodes (doubly-degenerate Weyl nodes)[72] in (Bi1−xInx)2Se3,[79,80] Na3Bi,[74,76,81,82] and Cd3As2[76,83–86] and Weyl nodes in the TaAs family.[87–91] The negative magnetoconductivity arising from the weak antilocalization has been observed recently in Bi0.97Sb0.03,[92,93] ZrTe5,[94] and TaAs.[88,95]
 | Fig. 6. Nontrivial band structure and Berry curvature of a topological semimetal. (a) A schematic of the energy spectrum of a topological semimetal. (kx, ky, kz) is the wave vector.  |
One of the low-energy descriptions of Weyl fermions in semimetals is

We calculate the magnetoconductivity arising from the quantum interference, as shown in Fig. 





 | Fig. 7. The magnetoconductivity δσqi(B) for different phase coherence length ℓϕ at ηI = η* = 0 (a), for different ηI at η* = 0 (b), and for different ηI at finite η* (c). The magnetic field B is applied along arbitrary directions. Parameters ℓ = 10 nm and ℓϕ = 1000 nm in panels (b) and (c). (d) The diagrams show the difference between ηI and η*, with ηI related to the intervalley scattering and η* measuring the intervalley correlation of intravalley scattering. The dashed lines represent the correlation of two scattering processes. ν = ± is the valley index. Adapted from Ref. [24]. |
Based on the theory in Ref. [24], we proposed a formula to fit the magnetoconductivity arising from the weak localization, and it has been applied in the experiment on TaAs[95]

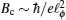

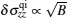
In the presence of the interaction, we find that the change of conductivity with temperature for one valley of Weyl fermions can be summarized as

 | Fig. 8. A schematic demonstration of the change of conductivity Δσ as a function of temperature T. We choose cee = cqi. Tc is the critical temperature below which the conductivity drops with decreasing temperature. Adapted from Ref. [24]. |
We find that the intervalley scattering and correlation can also lead to the weak localization. Two dimensionless parameters are defined for the inter- and intravalley scattering: 


In summary, we systematically studied the weak antilocalization and interaction-induced localization for Dirac and Weyl fermions in topological insulators and topological semimetals. With the help of Feynman diagram techniques, we considered the correction to the conductivity from the quantum interference correction and electron–electron interaction. We predicted the crossover between weak antilocalization and weak localization for the massive Dirac fermions. The theory can be applied to magnetically doped topological insulators and surface and bulk states in topological insulator thin films. With the help of an antidot nanostructure in topological insulator thin films, we verified the interaction induced localization tendency for Dirac fermions in topological insulators. We also studied the weak antilocalization and interaction effect in Weyl semimetals. For a single valley of Weyl fermions, we found that the magnetoconductivity is negative and proportional to the square root of the magnetic field at low temperatures, giving the signature for the weak antilocalization in three dimensions as well as for the Weyl fermion. In the presence of strong intervalley effects, we expected a crossover from the weak antilocalization to weak localization. In addition, we found that the interplay of electron–electron interaction and disorder scattering can also give rise to a tendency to localization for Weyl fermions.
Finally, we remark on the possible future works. On the weak localization induced by the interaction, the bulk and surface states still coexist on the Fermi surface in the latest experiment work. To show the interaction-induced localization of the surface states, further experiments are still needed to be performed in intrinsic topological insulators by doping[96] or using ternary and quaternary compounds.[97–103] Topological Weyl semimetals provide a new platform to study the weak antilocalization in three dimensions. Our formula of magnetoconductivity can be used for a systematic study of the transport experiments on topological semimetals. One of the interesting fields is the theories of the weak localization for semimetals with monopole charges higher than 1, as has recently been explored for the double-Weyl semimetals.[25] Also, the weak (anti-)localization theories for nodal-line and drumhead semimetal could be interesting topics for further research.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 | |
| 67 | |
| 68 | |
| 69 | |
| 70 | |
| 71 | |
| 72 | |
| 73 | |
| 74 | |
| 75 | |
| 76 | |
| 77 | |
| 78 | |
| 79 | |
| 80 | |
| 81 | |
| 82 | |
| 83 | |
| 84 | |
| 85 | |
| 86 | |
| 87 | |
| 88 | |
| 89 | |
| 90 | |
| 91 | |
| 92 | |
| 93 | |
| 94 | |
| 95 | |
| 96 | |
| 97 | |
| 98 | |
| 99 | |
| 100 | |
| 101 | |
| 102 | |
| 103 |


