Study of electron transport under the influence of disorder is at the heart of condensed matter physics. In a seminal paper published in 1958, Anderson pointed out that the prorogation of waves would be absent in a random media with sufficiently strong disorder.^[1] In the late-1970s, application of scaling analysis to the localization problem provided another major breakthrough in understanding the interplay between disorder and metal–insulator transition.^[2] An interesting outcome of the scaling theory is that no truly metallic state could exist in a two-dimensional (2D) electron system no matter how weak the disorder is.^[3] Even at the clean limit, interference between the time-reversed pairs of electron’s self-intersected trajectories leads to enhancement of backscattering probability, which is manifested as a lnT-type decrease in conductivity as temperature approaches to zero.^[3–5] Such a quantum correction to conductivity is referred to as weak localization (WL), a precursor to the Anderson localization that occurs at strong disorder. Many predictions on the 2D electron transport have been confirmed in experiment.^[5,6] Kravchenko et al., however, reported a possible metallic ground state in a low density Si-based 2D electron system, in which Coulomb interactions between electrons overwhelm electron’s kinetic energy.^[7,8] Despite a lot of attention drawn to this subject by this surprising observation, whether or not a truly metallic state can exist in 2D is still a controversial issue.^[9,10] This may be attributed to the formidable challenges in theoretical treatments of strong electron–electron interactions, as well as the experimental inability in reaching the absolute zero-temperature.

The recently discovered three-dimensional (3D) topological insulators (TIs) provide an interesting alternative to obtain truly metallic state in 2D.^[11,12] The surface of a 3D TI hosts gapless Dirac particles with spin directions locked perpendicularly to their momenta. Such spin-helical surface states are believed to be immune to localization.^[11,12] In the single-particle picture, this can be understood as a consequence of the Berry phase π associated with the spin-momentum locking, which leads to suppression of backscattering. This effect is opposite to the WL and thus termed as weak antilocalization (WAL). The topological protection against localization can survive even if the electron–electron interactions are present, according to a number of theoretical studies.^[13–16] The WAL effect has been observed in numerous magnetotransport measurements, in which the experimental hallmark is positive, cusp-shaped magnetoresistance that is strongly temperature-dependent at low temperatures.^[17–22] The connection between the positive magnetoresistance and the Dirac surface states is, however, not always straightforward due to a number of complications, such as the magnetoresistance of bulk carriers, the surface-bulk and inter-surface couplings, and the possible coexistence of topologically trivial surface states.^[23] Nevertheless, in the past several years there have been significant advances in suppressing the bulk conductivity by doping^[22,24] or alloying^[25–28] various TI compounds or by electrostatic gating.^{[17,18,20,21,29–31]} The magnetoresistance due to the WAL has become a sensitive probe to the surface transport and various couplings to the surface states.^{[17,18,20–22,30–33]}

In addition to the WAL, it is also possible to realize other interesting transport regimes by utilizing the hybridization between the top and the bottom surface states in ultrathin films of 3D TIs. These include the WL, the quantum spin Hall effect, topologically trivial insulating states, and so on.^[34–37] Evidence for the surface hybridization gaps has been reported from angular resolved photoemission spectroscopy (ARPES)^[38] and scanning tunneling spectroscopy.^[39] Transition from the WAL to the strong localization has been observed.^[40] Clear experimental evidence for crossover from the WAL to the WL, however, still remains elusive, even though negative magnetoresistances have been reported by several groups.^{[32,33,40,41]}

In this article, we give a short review of the latest experimental progress in the study of electron antilocalization and localization in 3D TIs and related structures. We do not intend to exhaustively describe all of the exciting results reported by many groups worldwide because of the limitation in space. We would rather focus on the experimental results reported in the last few years, which provide new insights into the electron localization in this fascinating class of materials. We hope that further efforts can be made to narrow the gaps between theory and experiment in this intriguing subfield of quantum transport. Readers may refer to Refs. [42]–[44] for more detailed summaries of the electron transport results prior to 2013 and Refs. [11], [12], [42], and [45] for more comprehensive reviews of TIs.

At low temperatures and in weak magnetic fields, magnetoconductivities in 3D TIs are often related to the WAL, which is a counterpart of the WL occurring in ordinary electron systems with negligible spin–orbit coupling.^[5] Both the WAL and the WL require the transport to be in diffusive regime, in which the sample’s size L, dephasing length l_ϕ and mean free path l_e satisfy L ≫ l_ϕ ≫ l_e at low temperatures. In addition, the diffusive regime also requires k_Fl_e ≫ 1, which corresponds to a sheet resistivity (or resistance per square in 2D) ρ_xx = (k_Fl_e)⁻¹(h/e²) ≪ h/e². Elastic scatterings by the disorder potential lead to quantum corrections to the electron conductivity. For the WAL (WL), the corrections in resistivity are negative (positive), which can be attributed to the destructive (constructive) interferences between electron waves propagating along the time-reversed pairs of self-crossing loops, as illustrated in Fig. 1(a). The WAL (WL) effect can be manifested in either the temperature dependence or the magnetic field dependence of conductivity. Increasing temperature leads to a decrease in the electron’s dephasing length and, hence, suppression of WAL (WL). This results in a logarithmic temperature dependence of conductivity, which has been observed in many experiments.^[20,46–49] Unfortunately, electron–electron interactions also produce a lnT-type correction to conductivity with comparable magnitude.^[50] This greatly complicates the analysis of the temperature dependent data. On the other hand, the physics of magnetoconductivity is more straightforward, since it falls into the territory of single particle physics. The decrease (increase) in conductivity with increasing magnetic fields can be understood as a result of Aharonov–Bohm phase introduced to the self-crossing loops, which reduces the effect of destructive (constructive) interferences.^[5] Significant suppression of the WAL (WL) effect is expected if the magnetic flux piercing through an area of is comparable to one flux quantum (h/e). In low magnetic fields, the magnetoconductivity, defined as Δσ(B) = σ_xx(B) − σ_xx(0), can be written as a simplified form of the Hikami–Larkin–Nagaoka equation^[51]

Fig. 1.

Figure Option ViewDownloadNew Window

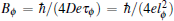
Fig. 1. Diffusive transport and weak antilocalization (WAL). (a) Illustration of a time-reversed pair of electron trajectories on a self-crossing loop. Destructive and constructive interferences between them lead to weak antilocalization and weak localization (WL), respectively. (b) Sketch of the band diagram of a topological insulator with Fermi energy EF located in the bulk conduction band. When EF is in the shaded regions, scatterings between the bulk and the surface states make the sample behave like a single-channel system in the phase coherent transport. (c) Extracted α values from fitting the low field magnetoconductivity data to the simplified HLN equation [Eq. (1)], which are nearly independent of the sheet electron density ne. (d) Prefactor α plotted as a function of mobility μ. Panels (c) and (d) are adapted from Ref. [20].

Early transport studies of TI thin films were mostly focused on Bi₂Se₃ and Bi₂Te₃, in which the Fermi level is not located inside the bulk band gap due to various defects [see Fig. 1(b)], and the bulk carriers contribute substantially to the transport.^[24] Considering the transport involving three possible channels, i.e., the top surface, the bottom surface, and the bulk layer, at first sight one would expect a deviation of the α value from 1/2. In experiment, however, it was found that the magnetoconductivity data could often be well-fitted to Eq. (1) with α values close to 1/2. For instance, Chen et al. obtained α ≈ 1/2 for Bi₂Se₃ thin films with sheet electron densities varied by one order of magnitude, as shown in Fig. 1(c).^[20] Kim et al. later reported similar α values for Bi₂Se₃ thin films with a wide range of thicknesses.^[52] Because of the conducting bulk, it is not possible to attribute the observed α ≈ 1/2 to the transport on a single surface. The strong scatterings between the surface and the bulk states make the multiple-channel system behave like a single channel transport.^[20] This can be described by the phase coherent transport models initially developed by Raichev and Vasilpoulos for coupled bilayer 2D electron systems in traditional semiconductor heterostructures^[53] and recently adapted by Garate and Glazman to topological insulators.^[54]

For an ideal 3D TI thin film, in which the bulk is insulating and the thickness is sufficiently large so that hybridization between the top and the bottom surfaces is negligible, the transport takes place in two independent channels. If the dephasing fields of these two surfaces can be tuned equal to each other, one would expect α = 1. Electrostatic gating is a necessary tool to obtain such smoking-gun evidence for the surface WAL effect. Many methods have been proven effective in depleting excessive bulk carriers,^[55] such as back-gating with SrTiO₃^[17] or SiO₂^[18] and top-gating with Al₂O_x grown with atomic layer deposition^[32] or liquid electrolytes.^[56] In 2011, Chen et al. and Checkelsky et al. independently reported observation of the crossover from α ≈ 1/2 to α ≈ 1 in back-gated Bi₂Se₃ thin films (or exfoliated thin plates).^[18,20] It is noteworthy, however, that tuning Bi₂Se₃ samples into the decoupled two-channel transport is very difficult because of high densities of bulk electrons. Despite a lot of work worldwide, there have been only a handful of reports of α ≈ 1 in Bi₂Se₃, and one of them has relied on doping in the bulk or on the top surface.^[33] More recently, successful syntheses of ternary compound (Bi,Sb)₂Te₃ and quarterly compound (Bi,Sb)₂(Se,Te)₃ have made the surface-dominated transport much easier to access.^[26–29] High quality (Bi,Sb)₂Te₃ films have been grown with molecular beam epitaxy onto SrTiO₃ and InP substrates.^[30,57] These films are particularly suitable for the study of the localization-related physics because the samples sizes can be readily made much larger than electron’s dephasing length. In contrast, nanoplates exfoliated from (Bi,Sb)₂(Se,Te)₃ single crystals are usually on the micrometer scale, and in some samples universal conductance fluctuations become pronounced.^[58,59] A large range of tuning of the chemical potential can be obtained in gated (Bi,Sb)₂Te₃ and (Bi,Sb)₂(Se,Te)₃ structures on a regular basis, and many groups have reported characteristics of ambipolar transport and large α values.^{[27,30–32,60]} Figure 2 shows the data of a (Bi,Sb)₂Te₃ thin film and a Bi₂Te₃ film grown on SrTiO₃ exhibiting decoupled two-channel transport at certain gate voltages.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. Obtaining decoupled surface transport by gating. (a)–(b) Gate-voltage dependences of sheet resistivity ρxx and Hall coefficient RH for a (Bi1−xSbx)2Te3 (BST) thin film [panel (a)] and a Bi2Te3 (BT) thin film [panel (b)]. Both films are 10 nm thick and can be tuned into ambipolar regime. (c) Magnetoconductivities of the BST film (symbols) and their best fits to the Eq. (1) (lines) for a set of gate voltages. The curves for gate voltages other than −20 V are shifted vertically for a clearer view. (d) Gate-voltage dependence of the extracted α for both samples. Here, VG0 is the gate voltage at which RH = 0, and may be approximately regarded as the charge neutrality point. The insets show the schematic band diagrams for the case of strong bulk-surface coupling. All of the data were taken at T = 1.6 K.

In the Anderson (strong) localization regime, electron wavefunctions are localized around certain positions in the form of |ψ(r)| ≈ exp(−|r − r₀|/ξ), where the localization length ξ satisfies ξ < l_ϕ.^[2,61] Theories have predicted surface states of truly 3D TIs are immune to the strong localization.^[13–16] In ultrathin TI films, the hybridization effect between the top and the bottom surfaces can open an energy gap near the Dirac point, resulting in a ground state of either a quantum spin Hall insulator or a topological trivial semiconductor.^[34–36] This makes observation of the strong localization in ultrathin TI films possible if one can tune the chemical potential into or close to the hybridization gap and makes the bulk insulating. However, as pointed out by Skinner et al., the bulk resistivity is very difficult to remove completely, even in well-engineered, highly compensated TI samples, such as (Bi,Sb)₂Te₃, and the best situation that one could get is the variable range hopping transport involving poorly screened electron and hole puddles.^[62]

Even though ARPES measurements have provided evidence for sizable surface hybridization gaps (e.g., as large as 0.2 eV for a few nm thick Bi₂Se₃ films) as early as 2009,^[38] clear observation of the strong localization has not been reported until recently.^[40] This was demonstrated with ultrathin (Bi, Sb)₂Te₃ thin films. With a combination of precise control of thickness and gate-voltage tuning of chemical potential, the transport can be varied from the well-defined diffusive regime to the variable range hopping regime. As shown in Fig. 3(a), the zero-field resistivity has a lnT-type temperature dependence in the diffusive regime and the corresponding magnetoconductivity exhibits the typical WAL behavior. When the chemical potential is tuned closer to the hybridization gap, the resistivity increases to the values comparable to 1 h/e²(≈ 26 kΩ) and a deviation from the lnT-type dependence takes place [Fig. 3(b)]. When the resistivity is increased further to the MΩ level, it follows ρ_xx ∝ exp[(T₀/T)^1/3], indicating a Mott-type variable range hopping transport. The low field magnetoconductivity in this strong localization regime is negative, and has a much smaller magnitude than that in the WAL regime [Fig. 3(c)].

Similar positive magnetoconductivities have also been observed in conventional 2D electron systems in the hopping regime.^[63–65] For instance, Hsu et al. reported a crossover of magnetoconductivity from negative to positive values when the resistivity of Ag–Ge thin films exceeds πh/e²(∼ 80 kΩ).^[65] In the hopping regime, electron transport is dominated by quantum interferences between different paths for forward scatterings because of the localized nature of electron wavefunctions.^[66,67] The phase differences between various trajectories are modified by an applied magnetic field. The positive magnetoconductivity can, hence, be regarded as a delocalization effect of the magnetic field. This effect is independent of the strength of SOC.^[65–67] Quantitatively, one expects Δσ ∝ B² in sufficiently low fields and saturates at a sufficiently high magnetic field.^[64–67] Figures 4(a)–4(c) show the magnetoconductivity data for a 2 nm thick (Bi, Sb)₂Te₃ sample in the strong localization regime.^[40] The sheet resistivity ρ_xx can be varied by increasing the gate voltage, which reduces the density of the hole carriers. The low field magnetoconductivity turns positive when ρ_xx is larger than 0.5 MΩ. A crossover from the negative to positive magnetoconductivity has also been observed in a 3 nm thick Bi₂Se₃ sample. As shown in Fig. 4(d), the onset of positive magnetoconductivity takes place at a gate voltage between 5 and 10 V, corresponding to a sheet resistivity of about 0.4 MΩ. Both crossover values (ρ_xx ≈ 0.5 MΩ and 0.4 MΩ) observed in TI thin films are considerably larger than πh/e²(∼ 80 kΩ), which has been argued by Hsu et al.^[65] to be a universal value separating the weak localization and the strong localization.

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. Transition from weak antilocalization (WAL) to strong localization in ultrathin TI thin films. (a) In the diffusive transport regime, the zero-field conductivity σ has a logarithmic dependence on temperature, and the magnetoconductivity shows the WAL behavior described by Eq. (1). (b) In the intermediate transport regime between the WAL and the strong localization, the magnetoconductivity is still negative but the magnitude is reduced significantly. (c) In the strong localization regime, the low field magnetoconductivities are positive and the zero-field sheet resistivity follows ρxx ∝ exp(T1/3), suggesting the transport in the variable range hopping regime. Adapted from Ref. [40].

Fig. 4.

Figure Option ViewDownloadNew Window

Fig. 4. Positive magnetoconductivity in the strong localization regime. (a) Gate voltage dependence of zero-field sheet resistivity ρxx of a 2 nm thick BST film. (b) Magnetoconductivity curves of the same sample for three representative ρxx values, which are marked as points A–C in panel (a). (c) Magnetoconductivity curves of the 2 nm BST thin film in the variable range hopping regime at selected temperatures. The sheet resistivity is ρxx = 2.3 MΩ at 1.6 K. Panels (a)–(c) are adapted from Ref. [40]. (d) Magnetoconductivity curves of a 3 nm thick Bi2Se3 sample for a set of gate voltages. The inset shows the gate voltage dependence of ρxx.

In addition to a possible transition to the quantum spin Hall state, the hybridization of the surface states in ultrathin 3D TI films may also lead to other interesting physics. For instance, Lu et al. pointed out that the spin texture of massive surface states [see Fig. 5(a)] can modify electron’s Berry phase significantly, if the chemical potential is comparable to the size of the hybridization gap Δ.^[37] It is interesting to note that similar physics can also occur for massive surface states formed due to magnetic exchange interactions.^[37,68] In both cases, the Berry phase follows ϕ = π(1 − Δ/2|μ|), where the chemical potential μ is measured from the center of the hybridization gap. A crossover from the WAL to the WL is thus expected to take place when Δ/2|μ| is increased toward 1.

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. Sketch of the gapped helical surface states of TIs and the predicted crossover from the WAL to the WL when the ratio Δ/E is varied from 0 to 0.999. (b) Prefactor α obtained from the fit to the simplified HLN equation [see Eq. (1)], which is plotted as a function of the sheet resistivity ρxx for four gate-tunable ultrathin Bi2Se3 or (Bi,Sb)2Te3 films. The data extracted from the experiment are shown in symbols, and the line is a theoretical curve that takes the disorder effect into account.[70] All of the raw data were taken at T = 1.6 K. Panel (a) is adapted from Ref. [37] and panel (b) from Ref. [40].

Several groups have reported magnetotransport results of ultrathin TI films, in which the magnitude of magnetoconductivity is much smaller than that of the standard WAL effect observed in thicker films.^{[32,33,40,41]} In most cases, the low field magnetoconductivity remains negative and can be fitted with the simplified HLN equation [see Eq. (1) in Section 2] quite well. The extracted α values are smaller than 1/2, the minimum value for the WAL even if the coherent coupling between various conducting channels is considered. It would be tempting to relate these reduced α values as a signature for the crossover from the WAL to the WL. However, the suppression of the WAL effect observed in these experiments are often accompanied with large sheet resistivities (e.g., ρ_xx > 10 kΩ) such that the transport is no longer in the well-defined diffusive regime. Strictly speaking, one would need ρ_xx < 5 kΩ (or equivalently k_Fl_e > 5) in order to ensure the transport being in the weakly disordered regime, in which electron’s localization length exceeds the dephasing length. Figure 5(c) compiles the α values of four gate-tunable ultrathin Bi₂Se₃ or (Bi,Sb)₂Te₃ samples. This clearly shows that a close correlation between the reduction in the α value and the increase in effective strength of disorder. The α value decreases substantially as ρ_xx becomes larger than 10 kΩ and nearly vanishes when ρ_xx approaches 100 kΩ. Furthermore, as mentioned in the previous section, positive magnetoconductivities have only been observed in the strong localization regime (i.e., k_Fl_e < 1/5) in our TI samples.^[40,69] Putting these results together, we conclude that the suppression of the WAL (or reduced α values) observed with disorder in the intermediate range (i.e., 5 kΩ < ρ_xx < 100 kΩ)^[70] cannot be attributed to the crossover to the WL in the gapped helical states. It is rather a disorder-related effect in the crossover regime between the WAL and the strong localization. It is also noteworthy that some of the WL-like features previously reported for magnetically doped TI thin films or TI/magnetic insulator heterostructures were also accompanied with resistivity values beyond the well-defined diffusive regime.^[71,72] Therefore, caution should also be taken to include the disorder effects when discussing the physics of gapped surface states in such structures.

We have shown the important role of disorder in the phase coherent transport in 3D TI thin films. When the disorder is weak (k_Fl_e ≫ 1), the transport is diffusive and the magnetoconductivity can be well characterized by the WAL effect of coupled or decoupled multiple channels existing on the top and the bottom surfaces and possibly in the bulk. The advances in improving sample quality and gating techniques have allowed for surface-dominating transport detected with the magnetoconductivity in the WAL regime. In ultrathin TI films, much stronger disorder (k_Fl_e ≪ 1) can be realized, and the transport can be driven into the strong (Anderson) localization regime, in which variable range hopping and positive magnetoconductivity are observed. In the crossover regime between the WAL and the strong localization, a gradual suppression of the negative magnetoconductivity takes place as the sheet resistivity increases. The suppression of WAL is argued as a consequence of the disorder-related effect during the transition from the WAL to strong localization, instead of the crossover from the WAL to the WL. It should be noted, however, that the experimental results reviewed in this article do not exclude the existence of the Berry phase effect predicted by Lu et al. for the massive Dirac fermions due to surface hybridization.^[37] Further experimental effort in improving the quality of ultrathin TI films is needed to bring the transport into the well-defined diffusive regime in order to confirm the predicted crossover from the WAL to the WL.

In this article, we have limited our discussions to the transport in perpendicular magnetic fields. The phase coherent transport in parallel or tilted magnetic fields can also give valuable information of the TI samples, which are difficult to acquire with other techniques.^[73,74] Additional work is also needed for understanding the complicated results in those circumstances. As mentioned in the Introduction, this article is not intended to cover all of the important results in this rapidly developing field. For instance, manifestations of weak antilocalization and Aharonov–Bohm-like effect in TI nanoribbons are not discussed.^[75–77] Readers may find many previous reviews valuable in obtaining a more comprehensive knowledge of this exciting research area.^{[11,12,43–45,78]}