† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project partially supported by the National Key Research and Development Program of China (Grant Nos. 2016YFA0302400 and 2016YFA0300604), partially by the National Natural Science Foundation of China (Grant Nos. 11274359 and 11422428), the National Basic Research Program of China (Grant No. 2013CB921700), and the “Strategic Priority Research Program (B)” of the Chinese Academy of Sciences (Grant No. XDB07020100).
We review the recent, mainly theoretical, progress in the study of topological nodal line semimetals in three dimensions. In these semimetals, the conduction and the valence bands cross each other along a one-dimensional curve in the three-dimensional Brillouin zone, and any perturbation that preserves a certain symmetry group (generated by either spatial symmetries or time-reversal symmetry) cannot remove this crossing line and open a full direct gap between the two bands. The nodal line(s) is hence topologically protected by the symmetry group, and can be associated with a topological invariant. In this review, (i) we enumerate the symmetry groups that may protect a topological nodal line; (ii) we write down the explicit form of the topological invariant for each of these symmetry groups in terms of the wave functions on the Fermi surface, establishing a topological classification; (iii) for certain classes, we review the proposals for the realization of these semimetals in real materials; (iv) we discuss different scenarios that when the protecting symmetry is broken, how a topological nodal line semimetal becomes Weyl semimetals, Dirac semimetals, and other topological phases; and (v) we discuss the possible physical effects accessible to experimental probes in these materials.
Topological semimetals (TSM) are defined as systems where the conduction and the valence bands cross each other in the Brillouin zone (BZ), and the crossing is non-accidental, i.e., cannot be removed by perturbations on the Hamiltonian without breaking any of its symmetries. If there be no symmetry, two bands, when close in energy, will hybridize with each other and maintain a gap in-between, through a mechanism known as the band repulsion; however, in the presence of certain symmetries (e.g., crystalline symmetries and time-reversal symmetry), the two crossing bands may have different quantum numbers such that they cannot be hybridized. From this, we see that all band crossings, hence all topological semimetals, can only be protected by symmetries and hence belong to symmetry protected topological phases of matter.
In three dimensions (3D), two bands can cross each other either at discrete points or along a closed curve. In the former case, there are Weyl semimetals[1,2] and Dirac semimetals[3] that have been intensively studied in theory as well as in experiment. In the latter case, the curve where the bands cross is called a nodal line,[4] which may either take the form of an extended line running across the BZ, whose ends meet at the BZ boundary,[5] or wind into a closed loop inside the BZ,[6] or even form a chain consisting of several connected loops (nodal chain).[7] Topological semimetals with such line band crossings are called topological nodal line semimetals (TNLSM). In principle, one may have TNLSM in both quasi-2D[8] and 3D systems,[9,10] and in this review, we will focus on the latter.
In a topological gapped phase, such as Chern insulator, topological insulator or topological crystalline insulator, the nontrivial topology of the bands can be characterized by a topological invariant, a quantum number that depends on the Bloch wave functions of the valence bands as a whole. The form of the topological invariant is determined by only two factors: dimension and symmetry. Similarly for a topological semimetal, one can also associate with each band crossing (either a point node or a line node) a topological invariant, whose form depends on the symmetry group that protects the nodal structure. Given the dimension of the node and the symmetry group that protects it, one or several topological invariants can be found, and these quantum numbers provide a full topological classification of the nodes. Up to this day, the classification of TNLSM is yet to be complete. Theoretically, people have found mirror reflection protected nodal lines with a Z-invariant,[6,11–14] nodal line protected by inversion, time-reversal and spin rotation symmetries with two Z2-invariants,[5,15–26] screw rotation protected double nodal lines (to be defined later) with a Z-invariant,[29] etc.
While a topological classification tells us how many topologically different types of nodes exist in systems with a given symmetry group, only numerical calculation, mainly first-principles calculations that compute the band structure and Bloch wave functions, can compute this invariant in a given compound and determine if it is a TSM or not. The calculation has proved more challenging than that of the topological invariant in a gapped system, because of (i) the slow convergence in a gapless system and the fact that (ii) the band crossing point is not always at a high-symmetry point, but along a high-symmetry line or even on a high-symmetry plane. We will review numerical efforts that have resulted in the proposals of various materials systems as TNLSM protected by different symmetry groups.
When the protecting symmetry is broken in a TNLSM, the nodal line is either fully gapped or gapped into several nodal points. For example, without spin–orbital coupling (SOC), TaAs was,[30,31] in first-principles calculation, shown to be a TNLSM protected by mirror reflection and spin-rotation symmetries with two nodal lines, and when SOC was turned on, each nodal line is gapped into three pairs of Weyl nodes. Another example is the double nodal line in SrIrO3, which is gapped into a pair of non-symmorphic Dirac nodes when a certain mirror reflection symmetry is broken.[27,32] Therefore, understanding how a nodal line evolves upon symmetry breaking can help predict new topological materials.
Unlike most topological phases, TNLSMs in general do not have protected boundary modes.[28] Therefore, identifying them in experiments poses a challenge to the experimentalists. Angle resolved photoemission spectroscopy (ARPES) has been used to resolve the nodal band structure in the bulk,[11,12] but the limited momentum resolution in the perpendicular direction prevents these efforts from being deterministic. Quantum oscillation measurements[33] were performed to map the Fermi surface of ZrSiSe and ZrSiTe as well as the Berry phase along a closed loop on the Fermi surface, partially supporting the proposal of TNLSMs in these materials. Another unanswered question is the fate of these materials in the presence of electron correlation. It has been proposed that the screening effect is qualitatively different from that in normal metals,[34] and that in the presence of strong electron interaction, the quantum phase transition from a TNLSM to a nodal point semimetal or a gapped system belongs to a new universality class.[35]
Below is the outline of the review. In Section 2, we briefly go through the topological classification of TNLSM protected by several symmetry groups by writing down the expression of the topological invariants in terms of the Bloch wave functions. In Section 3, we review the several materials proposed by first principle calculations to be TNLSMs. In Section 4, we discuss various scenarios of how the nodal line evolves when the protecting symmetry is broken. In Section 5 we discuss the experimental consequences and the many-body effects in TNLSMs so far proposed in the literature.
Topological invariant gives a quantitative description of the topology of a system. Let us first review its definition in a ‘gapped’ band structure, where ‘gapped’ means that at each momentum
For TSM, the definition of topological invariant needs modification as we cannot have a well-defined conduction or valence bands throughout the BZ: at some points the two bands cross each other. Given a nodal structure, say a point node, in BZ, we first use an imaginary manifold to enclose without touching the node. On the enclosing manifold, the conduction and the valence bands do not touch each other, having a full direct gap. Therefore, topological invariants can be defined on the enclosing manifold and we identify this invariant as the topological invariant of the node inside. We use the example of Weyl point to illustrate this process,[1] which is the same one used in numerics to calculate the monopole charge of a Weyl point.[2,30] Given a Weyl point, we consider a sphere in k-space to enclose this point (here one needs to make sure that only one band crossing point is inside). Then since the bands are ‘gapped’ on the surface of the sphere, we can calculate its Chern number. When the Chern number is ±1, we know that the Weyl point has monopole charge of ±1; if the Chern number is ±2, we know that the nodal point is actually a double-Weyl point[42] with monopole charge of ±2. Another example we use is the Dirac point protected by C4v (existing in, e.g., Cd3As2[43]). Here since the Dirac point is only allowed to move along the kz-axis in the BZ, we consider two points p1,2 along the kz-axis above and below the Dirac point, to enclose the Dirac point. At p1 and p2, the conduction and the valence bands are separated, and each band is double degenerate with C4 eigenvalues e±iπ/4 or −e±iπ/4. At p1,2 we count the number of valence bands that have C4 eigenvalue e±iπ/4, denoted by N1,2, respectively. The topological invariant of the Dirac point is given by z = N1 − N2.[46,47]
For TNLSMs, we have three types of enclosing manifolds, being zero-dimensional, one-dimensional, and two-dimensional, respectively. If the nodal line is fixed by symmetry (usually a mirror reflection symmetry) to some high-symmetry plane, we choose two points on the same plane, on different sides of the nodal line, respectively (see Fig.
In real space, a mirror reflection symmetry can be defined as
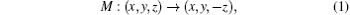

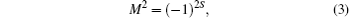
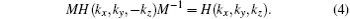
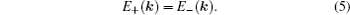
Since the nodal line is fixed to the high-symmetry planes by mirror symmetry, we use the zero-dimensional enclosing manifold. On the two sides of the nodal line we pick two points p1 and p2. At p1,2, the conduction and the valence bands are separated in energy, and one can count the number of bands below the Fermi energy that has mirror eigenvalue of +1, denoted by N1,2. The topological invariant is then given by
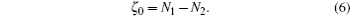
 | Fig. 1. Dispersion along a cut across the nodal lines protected by mirror reflection symmetries carrying different topological invariants. Different colors represent opposite mirror eigenvalues. (a) An accidental nodal line which has ζ0 = 0. (b) A protected nodal line carrying ζ0 = 1. (c) Two nodal lines (one inner and one outer) carrying opposite invariants. (d) Two nodal lines carrying the same invariant.[28] |
Here we first assume that all the three symmetries are present in our system. Since SU(2) is a symmetry, we can redefine time-reversal operator, combining it with a π spin rotation about the y-axis,
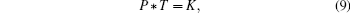

Away from the crossing lines, the Hamiltonian can be ‘flattened’ as
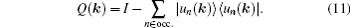
Before going further, a brief review of the concept of homotopy groups in algebraic topology is due. Consider continuous mappings from an n-sphere Sn to a space M (in this case the space of all occupied bands). If two such mappings, ϕ1 and ϕ2, can be continuously deformed into each other, then we say that ϕ1 and ϕ2 are equivalent to each other. Mappings that are equivalent to each other form an equivalent class, and each class corresponds to an element in the homotopy group, denoted by πn(M). For example, if the homotopy group has only one element, πn(M) = {e}, then we know that all mappings from Sn to M are equivalent to each other, and therefore equivalent to a trivial mapping where all points in Sn map to the same point in M. If the homotopy group is Z2, πn(M) = Z2, then we know that all mappings are either equivalent to a trivial mapping or to a nontrivial mapping. This mathematical definition can be paraphrased in our physical context: Sn≥1 is our enclosing manifold; M is the Hilbert space spanned by all occupied bands; the Hamiltonian H(
If Q(
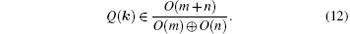
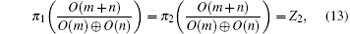
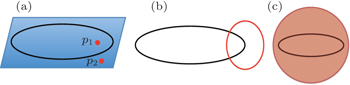 | Fig. 2. Manifolds of different dimensions (S0, S1, and S2) that enclose a nodal line. (a) Two points (S0) inside and outside the nodal line pinned to (protected by) a mirror plane; (b) a loop (S1) that threads the nodal line; and (c) a sphere (S2) surrounding the entire nodal line.[28] |
If ζ1 is zero, we infer that the line crossing is purely accidental and can be removed by an arbitrarily small perturbation that preserves all symmetries. Therefore, all topological nodal rings protected by this symmetry group must all have ζ1 = 1. The explicit expression of ζ1 is simply the Berry phase on the ring that links with the nodal line,
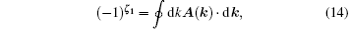
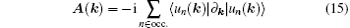
We have understood that ζ1 = 0 and ζ1 = 1 mean that the nodal ring is accidental and protected, respectively. What is the physical meaning of the second index? When the second index ζ2 is zero, although the nodal line is stable against perturbations, the nodal line may still shrink to a point and be gapped by a continuous tuning of the Hamiltonian. This point can be illustrated by the following example. Consider an effective Hamiltonian near Γ
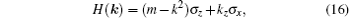

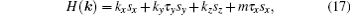
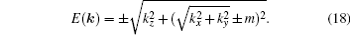
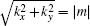
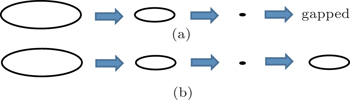 | Fig. 3. (a) By tuning m from positive to negative in Eq. ( |
One can draw an analogy between the ζ2 of the nodal line and the monopole charge of a Weyl point, as both are defined on a sphere that encloses the nodal structure, with a key difference that here the monopole charge is a Z2-charge in the former and Z-charge in the latter. This difference implies that when two nodal rings with ζ2 = 1 meet each other, they will necessarily annihilate each other, while two Weyl points with C = 1 will not annihilate each other, but form a double Weyl point. The Nelson–Nanomiya theorem also applies to this Z2-charge, which states that in a lattice model, the nodal lines with ζ2 = 1 must appear in pairs. This is another distinction between nodal lines with ζ2 = 0 and ζ2 = 1: while the ring can be annihilated or created in singles in the former case, in the latter case they can only be annihilated or created in pairs.
The explicit form of ζ2, in terms of the wave functions, is not very concise, and readers are encouraged to read the Appendices of Ref. [28] for more information. Here we give an intuitive understanding of this invariant. Since the Hamiltonian H(
Before closing this subsection, a few technical comments are due. (i) The first invariant ζ1 was first identified as a Z-invariant in the literature,[4] because the authors considered a two-band model, and π1(O(2)/O(1) ⨁ O(1)) is indeed Z. Physically, this means that if there are only two bands, two nodal lines of the same charge meeting each other will not gap out, but once more bands are introduced, they can meet with the two crossing bands and gap out the nodal line. (ii) Another special case is π2(O(4)/O(2) ⨁ O(2)) = Z, that is, when there are in total four bands and two conduction (valence) bands, the second index becomes a Z-index. This means that a nodal line may carry either positive or negative charges, and that two nodal lines with the same monopole charge will not annihilate each other, but when other bands are introduced into the model, the two nodal lines will be gapped when they meet each other.
Double-nodal lines appear when both the conduction and the valence bands are doubly degenerate and they cross each other along a nodal line, where the bands are fourfold degenerate. From its definition, we see that we need a symmetry such that the all bands are doubly degenerate, and then we need another symmetry to protect the band crossing.
Even for spin–orbit coupled systems, P * T makes sure that all bands are doubly degenerate. In the presence of SOC, we cannot redefine T such that T2 = +1, and therefore, we have

Intuitively, it is understood that it is harder for two degenerate bands to cross each other than for non-degenerate bands. Consider an effective theory near the band crossing, then one needs at least a four-band model for the former and a two-band model for the latter. A four-band model is expanded in fifteen Dirac matrices (the identity matrix having nothing to do with band crossings), while a two-band model in three Pauli matrices. Then a double-line nodal requires the coefficients of fifteen Dirac matrices to vanish and a single nodal line only requires the coefficients of three Pauli matrices to vanish. Corroborating with this intuition is the fact that mirror reflection symmetry M : (x,y,z) → (x,y,−z) is insufficient to protect the crossing.
For spinful systems, equation (
From this discussion, we may conjecture that in order for the two bands to have a protected crossing, we need the two subbands in a degenerate band to have the same quantum number of some symmetry. So far, one type of these symmetries have been found:[28] the twofold screw rotation, which acts in real space as
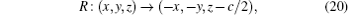
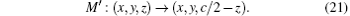
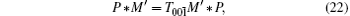
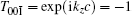
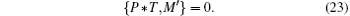
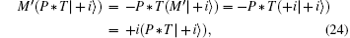
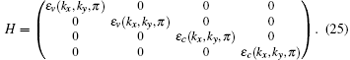
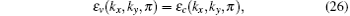
The topological invariant for the double-nodal lines is very similar to the case of single nodal lines protected by mirror reflection. Choose two points on the two sides of the double-nodal line, p1 and p2, and count the number of the occupied bands at p1,2 that have M′ = +i, and denote them by N1 and N2. The Z-invariant is given by
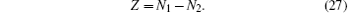
We have several technical comments before closing this subsection. To simplify our discussion, in Eq. (
Since TNLSM was proposed in 2011,[4] there have been many material proposals to realize it experimentally. According to the classification in the former section, we summarize, to the best of our knowledge, the existing proposals in Table
| Table 1. The proposed materials to host nodal lines classified. The DSM, WSM, and TI mean the nodal lines evolve into the corresponding topological state when spin–orbit coupling (SOC) is further included. N/A means unknown. Type-A means that the nodal lines are protected by mirror reflection symmetry; type-B means that the nodal lines are protected by space inversion and time-reversal symmetry; type-C means the existence of double-nodal lines. . |
We have established several classes of nodal lines protected by different symmetry groups. When these symmetries are partially or fully broken, the nodal lines generically vanish with them. However, unlike a point node that can simply gap out, there are at least two fates for a nodal line: it may break into several discrete nodal points, or it may also be fully gapped. In this section, we show (i) how a nodal line protected by mirror reflection and SU(2) spin rotation breaks into several Weyl points or Dirac points if SU(2) is broken and (ii) how the double-nodal line proposed in SrIrO3 breaks into two nonsymmorphic Dirac points when one glide reflection symmetry is broken.
As we have discussed at the end of Section 2, in a spinless (or SU(2)-symmetric) system, nodal line appears when there is a band inversion between two bands with opposite mirror eigenvalues. This has been seen in first principles calculations in many classes of materials. In reality, the spin–orbital coupling, while small, cannot be completely ignored in electronic systems. When SOC is considered, the band repulsion between opposite spins becomes nonzero at finite momenta, making the nodal line unstable. Depending on the remaining symmetries (other than SU(2)) of our system, the nodal line can either break into several pairs of Weyl points, one or several Dirac points, two separate nodal lines, or become fully gapped. In TaAs and several materials of the same family, it is found that a nodal line in the non-SOC band structure breaks into three pairs of Weyl points; in LaN, Cu3(Pd,Zn)N and CaTe, three intersecting nodal lines break into two Dirac points. In noncentrosymmetric materials, a nodal line in the non-SOC band structure usually signifies Weyl points when SOC is turned on.
How a nodal line breaks into Weyl points can be understood in simple effective models, but the quantitative results (say how many pairs of Weyl points and their location) will differ from those from the first-principles calculations. Consider an effective Hamiltonian for TNLSM protected by mirror reflection and SU(2)
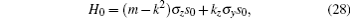
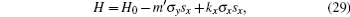
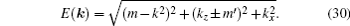
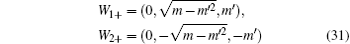
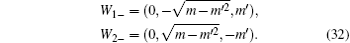
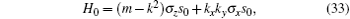
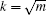
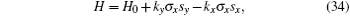
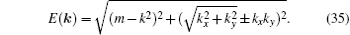
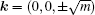
SrIrO3 is the first proposed material that has a double-nodal line, protected in this particular case by a twofold screw rotation about the b-axis Sy : (x,y,z) → (−x + a/2,y + b/2,−z + c/2) as well as inversion and time-reversal symmetries. The space group of the bulk material is generated by inversion P : (x,y,z) → (−x,−y,−z), Sy and Sx : (x,y,z) → (x+a/2,−y + b/2,−z). Now suppose we break Sy preserving P and Sx, the double-nodal line is no longer protected. However, one can prove that along UR, the subbands in a degenerate band have the same eigenvalues of Sx. To see this, we note that
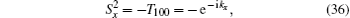
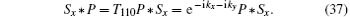
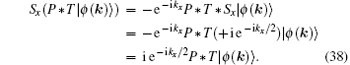
For most topological materials, the observation of topological surface states has been considered a definitive confirmation of the nontrivial topology in the band structure. The underpinning of this logic is the bulk-edge correspondence principle, which asserts that a nontrivial bulk topology in d-dimensional bulk must correspond to a gapless mode (d − 1)-dimensional edge, which cannot be realized in a real (d − 1)-dimensional system without symmetry breaking. Here we emphasize the prerequisites of its application that (i) the symmetry group protecting the topology in the bulk must be unbroken on the edge and (ii) the interaction is weak or the edge can still be gapped into an anomalous topology order.
So far, the protection of nodal lines requires one or several of the following spatial symmetries: mirror reflection, space inversion, and twofold screw rotation. A simple inspection of them shows that there is no surface where any of these symmetries is preserved. Therefore, the bulk-edge correspondence may not be applied here to indicate the existence of topological surface modes in TNLSMs. In numerical simulations. However, there are indeed states localized on the surface in the surface BZ, appearing inside the projections of the nodal lines. Unlike the surface states of, say, topological insulators, these surface states are very flat in dispersion, and are hence dubbed ‘drumhead’ states. The drumhead states can be considered as a higher-dimensional analogy of the flat band on the zigzag edge of graphene, and are hence dubbed ‘drumhead’ states, which may host interesting correlation effects due to the high ratio of interaction and kinetic energy.[54] As we have stated, the flat bands are not topologically protected: a change of the model parameters on the surface will destroy the ‘flatness’ of the surface modes, and can even push these surface states into the bulk continuum spectrum. In the same way the flat band on the zigzag edge gains dispersion as soon as we turn on the intra-sublattice hopping on the edge. The lack of a topological signature on the surface poses a challenge to design a ‘smoking gun’ experimental observation of TNLSM. In Refs. [11] and [12], using ARPES, the group measures the dispersion of both the bulk and the surface states, where the results support the existence of a nodal line protected by mirror reflection symmetry in PbTaSe2 and TlTaSe2.
Due to the lack of surface signatures in TNLSMs, people turn to the bulk probes. In quantum oscillation, the special behavior of these materials has been predicted and measured. In Ref. [55], the Landau levels of an effective
The ideal Fermi surface of a TNLSM is the nodal ring itself at half-filling, which may be achieved only if there is particle-hole symmetry or chiral symmetry that pins the energy of all the points on the nodal line at the Fermi energy. The dispersion near the Fermi surface is also particular in a TNLSM: while the band splitting along the nodal line is zero, the dispersion perpendicular to the nodal line is linear in momentum. These special properties near the Fermi energy lead to new many-body effects for TNLSMs. In Ref. [34], it is predicted that the Coulomb interaction is only partially screened and still long-ranged due to the vanishing density of states at the Fermi energy. In Ref. [35], the authors using renormalization group method analyze the quantum phase transition between a topological nodal line superconductor and a fully gapped superconductor, where the symmetry protecting the nodal line is broken. It is predicted that this transition belongs to a new universality class, where the dynamic exponent, order parameter exponent, and susceptibility exponent are all 1.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 |


