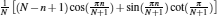† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11504340).
Inspired by the recently proposed Legendre orthogonal polynomial representation for imaginary-time Green’s functions G(τ), we develop an alternate and superior representation for G(τ) and implement it in the hybridization expansion continuous-time quantum Monte Carlo impurity solver. This representation is based on the kernel polynomial method, which introduces some integral kernel functions to filter the numerical fluctuations caused by the explicit truncations of polynomial expansion series and can improve the computational precision significantly. As an illustration of the new representation, we re-examine the imaginary-time Green’s functions of the single-band Hubbard model in the framework of dynamical mean-field theory. The calculated results suggest that with carefully chosen integral kernel functions, whether the system is metallic or insulating, the Gibbs oscillations found in the previous Legendre orthogonal polynomial representation have been vastly suppressed and remarkable corrections to the measured Green’s functions have been obtained.
The rapid development of efficient numerical and analytical methods for solving quantum impurity models has been driven in recent years by the unprecedented success of dynamical mean-field theory (DMFT)[1–3] and its non-local extensions.[4–6] In the framework of DMFT, the self-energy function is assumed to be local; i.e, its momentum dependence is completely neglected. Thus, the solution of the original lattice model may be obtained from the solution of an appropriately defined quantum impurity model plus a self-consistency condition. In order to solve the quantum impurity models, numerous quantum impurity solvers have been developed in the last few decades.[1,2] In particular, the recently developed continuous-time quantum Monte Carlo impurity solvers[7–12] are being more generally preferred due to their accuracy, efficiency, and ability to treat extreme low temperature and arbitrary interaction terms in the quantum impurity models.
Among various continuous-time quantum Monte Carlo algorithms, the hybridization expansion version (abbreviated CT-HYB)[8–10] is up to now the most powerful and reliable impurity solver and it is widely used. However, for the CT-HYB quantum impurity solver, several severe technical limits still remain. One well-known problem is the high frequency noise commonly observed in the Matsubara Green’s function G(iωn) and the self-energy function Σ(iωn).[13,14] Similar problems also arise in the calculations of imaginary-time Green’s functions G(τ) and two-particle vertex functions Γ(ω, ω′, ν),[15] which are less emphasized in the literature, according to our knowledge. In order to cure these problems, an intuitive and straightforward idea is to run more statistics in the Monte Carlo simulations to suppress the data fluctuations as far as possible. Actually, although this strategy mitigates the problems, it will not avert them and will deteriorate the efficiency of the CT-HYB quantum impurity solver rapidly.
Recently, Lewin Boehnke et al.[16] suggested to measure the single-particle and the two-particle Green’s functions in the basis of Legendre orthogonal polynomials. The Legendre orthogonal polynomial method provides a much more compact representation of Green’s functions than standard Matsubara frequencies and, therefore, significantly reduces the memory requirement for these quantities. Moreover, it can be used as an efficient noise filter for various physical quantities within the CT-HYB quantum impurity solver since the statistical noise is mostly carried by the high-order Legendre coefficients which should be truncated, while the physical properties are largely determined by the low-order coefficients which should be retained. By using the Legendre orthogonal polynomial representation, the accuracy of the CT-HYB quantum impurity solver is greatly improved. This representation has been broadly used in the computations of the single-particle Green’s function and lattice susceptibilities in the context of realistic DMFT calculations in combination with the density functional theory.[17,18]
It seems that the Legendre orthogonal polynomial representation is superior to the old one. However, according to careful examination, we find that the so-called Gibbs oscillations appear quite easily in the calculated Green’s functions and other physical quantities, which could be due to the rough truncation of the Legendre basis. The character of the Gibbs oscillations is that the calculated physical quantities are smooth but oscillating periodically with the scattered direct measurements. The situation is even worse when the system is in the insulating state where the Gibbs oscillations will likely cause the reconstructed single-particle Green’s function to break the causality. Note that a common procedure to damp these oscillations relies on an appropriate modification of the expansion coefficients by some integral kernel functions, which is the well-known kernel polynomial representation.[19] Motivated by this idea, in this study we adopt the kernel polynomial method (dubbed KPM) to improve the measurement of the single-particle and two-particle quantities for the CT-HYB quantum impurity solver. We find that significant improvements are gained, and the kernel polynomial representation is better than the Legendre orthogonal polynomial representation, no matter whether the system is metallic or insulating.
The rest of this paper is organized as follows. In Subsection 2.1, a brief introduction to the orthogonal polynomial representation is provided. The original implementation is based on the Legendre polynomials only. Here we generalize it to the Chebyshev polynomials. In Subsection 2.2, the kernel polynomial representation is presented. In Section 3, we benchmark the KPM by re-examining the imaginary-time Green’s functions G(τ) for the single-band Hubbard model with half-filling. The characteristics of different integral kernel functions which are used to adjust the expansion coefficients are discussed in detail. Section 4 gives a conclusion and outlook.
In principle, the imaginary-time Green’s function G(τ) (τ ∈ [0, β]) can be expanded in terms of orthogonal polynomials defined on the interval [−1, 1], such as the Legendre polynomials Pn(x),
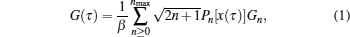
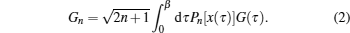
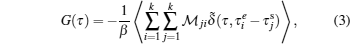
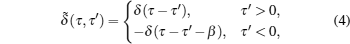
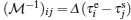
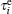
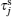
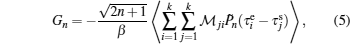
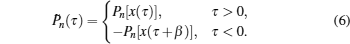
Lewin Boehnke et al.[16] have chosen the Legendre orthogonal polynomials as their preferred basis to expand the single-particle and the two-particle Green’s functions. But it should be emphasized that a priori different orthogonal polynomial basis is possible as well. Thus we would like to generalize the approach to use the Chebyshev orthogonal polynomials as an optional basis. It is well-known that there exist two kinds of Chebyshev polynomials.[20] Here we choose the second kind Chebyshev polynomials Un(x) as the basis because their orthogonal condition is simpler. Then, we reach the following expressions:
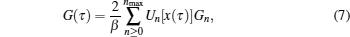
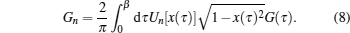
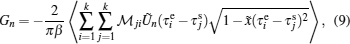


Virtually, the CT-HYB quantum impurity solver can directly accumulate the Legendre or Chebyshev expansion coefficients Gn instead of the original Green’s functions G(τ). Once the Monte Carlo sampling has been finished, G(τ) can be reconstructed analytically via the expansion coefficients (see Eqs. (
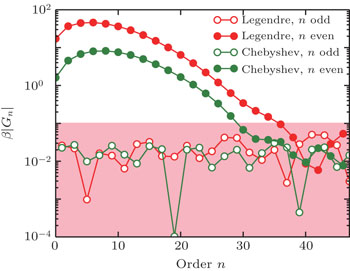
As we already know, the essential idea of the orthogonal polynomial method is to expand G(τ) and the other physical observables in infinite series of Chebyshev or Legendre polynomials, and then use the Monte Carlo algorithm to sample the expansion coefficients Gn directly. However, the infinite expansion series will remain finite actually from a numerical perspective (n ≤ nmax), and we are thus trapped by a classical problem of approximation theory. In this case, the problem is equivalent to figure out the best approximation to G(τ) given a finite number of Gn. Experience shows that a crude truncation of the infinite series probably leads to poor numerical precision and fluctuations, which is also known as Gibbs oscillations in the literature.[19] Later, we will see that as for the reconstructed Green’s function G(τ) in the insulating state, almost periodic Gibbs oscillations are clearly identified in a wide τ range.
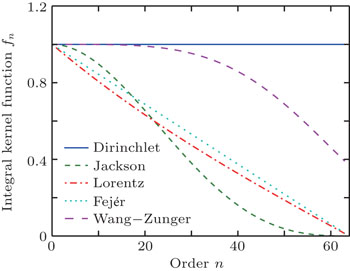
The KPM is an efficient approach to systematically damp the Gibbs oscillations. Its spirit is to introduce some kind of integral kernel function fn, and then the expansion coefficients are modified from Gn to Gnfn.[19] The fn decreases monotonously with respect to n and satisfies 0.0 ≤ fn ≤ 1.0, so as to Gn fn → 0.0 when n → ∞. In order words, fn can be considered as a damping factor. Obviously, the simplest integral kernel function, which is usually attributed to Dirichlet, is obtained by setting fn ≡ 1. By using the Dirichlet kernel, the KPM is equivalent to the previous orthogonal polynomial method. In addition to the Dirichlet kernel, there also exist many other integral kernel functions, such as Jackson, Lorentz, Fejér, and Wang–Zunger kernels. Their formulas are collected in Table
Finally, we note that the integral kernel functions fn can be evaluated and stored in advance, so that the KPM has no effect on the computational efficiency of the CT-HYB quantum impurity solver. The implementation of KPM is very simple, only trivial modifications are needed for the orthogonal polynomial representation version of CT-HYB quantum impurity solver, i.e., replacing Gn by Gnfn. Since both the kernel polynomial and orthogonal polynomial representations are only alternate bases for the single-particle and two-particle quantities, they can be implemented in the segment picture[8] and general matrix[9] formulations of CT-HYB quantum impurity solvers to improve the numerical accuracy and efficiency. We have implemented the kernel polynomial and orthogonal polynomial representations (using the Legendre and Chebyshev orthogonal polynomials) in a generic quantum impurity solver package iQIST.[21]
| Table 1. Collection of various integral kernel functions fn that can be used to improve the quality of an order-N Legendre or Chebyshev series. . |
In this section we will try to benchmark the kernel polynomial representation and compare the calculated results with those obtained by the orthogonal polynomial representation[16] and conventionally direct measurements.[8] For the sake of simplicity, a single-band Hubbard model with half-filling is chosen as a toy model to examine our implementations. The Hamiltonian of the single-band Hubbard model reads
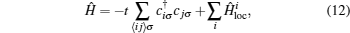
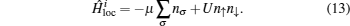
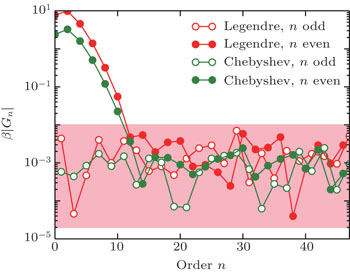
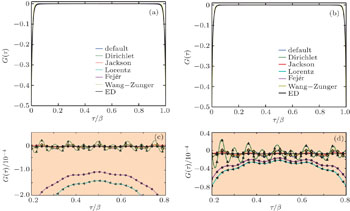
Let us first concentrate our attention on the metallic state. In Fig.
Figure
Now let us turn to the insulating state. When U = 6.0 and β = 50, a definitely insulating solution is obtained within DMFT. The “bare” Legendre and Chebyshev coefficients β|Gn| of G(τ) are shown in Fig.
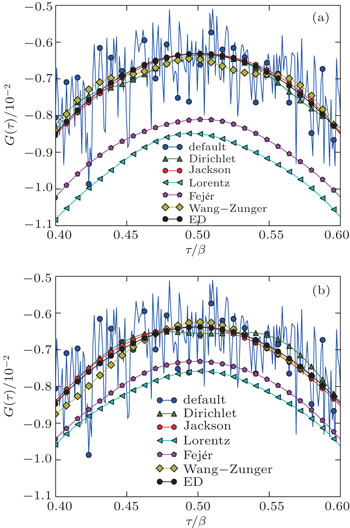
The calculated imaginary-time Green’s function G(τ) by using KPM with different orthogonal polynomials and integral kernel functions are illustrated in Fig.
It is suggested that the orthogonal polynomial method based on the Legendre orthogonal polynomials can be used to improve the accuracy and computational efficiency of the CT-HYB quantum impurity solver,[16] but it still suffers from the Gibbs oscillations since the number of polynomial expansion coefficients is limited. In this paper, we develop a better representation to cure this problem.
At first, we generalize the original orthogonal polynomial method to using the second kind Chebyshev orthogonal polynomials. We find that the Chebyshev polynomials require fewer expansion coefficients to reach the converged results, and thus are better than the Legendre polynomials in computation efficiency. Second, we believe that the KPM with carefully chosen integral kernel functions could be used to suppress the Gibbs oscillations observed in the single-particle Green’s functions obtained by the orthogonal polynomial method and improve the numerical accuracy further. According to the benchmark results for the single-band half-filled Hubbard model, it is demonstrated that the Jackson kernel function is the optimal choice for imaginary-time Green’s function G(τ). Finally, though the KPM presented in this paper is mainly developed for the CT-HYB quantum impurity solver, it can be easily generalized to other continuous-time quantum Monte Carlo impurity solvers.[7] Besides the imaginary-time Green’s function, this method can be applied to the other physical observables, such as Matsubara Green’s function G(iωn) and self-energy function Σ(iωn), the generalization is straightforward.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 |