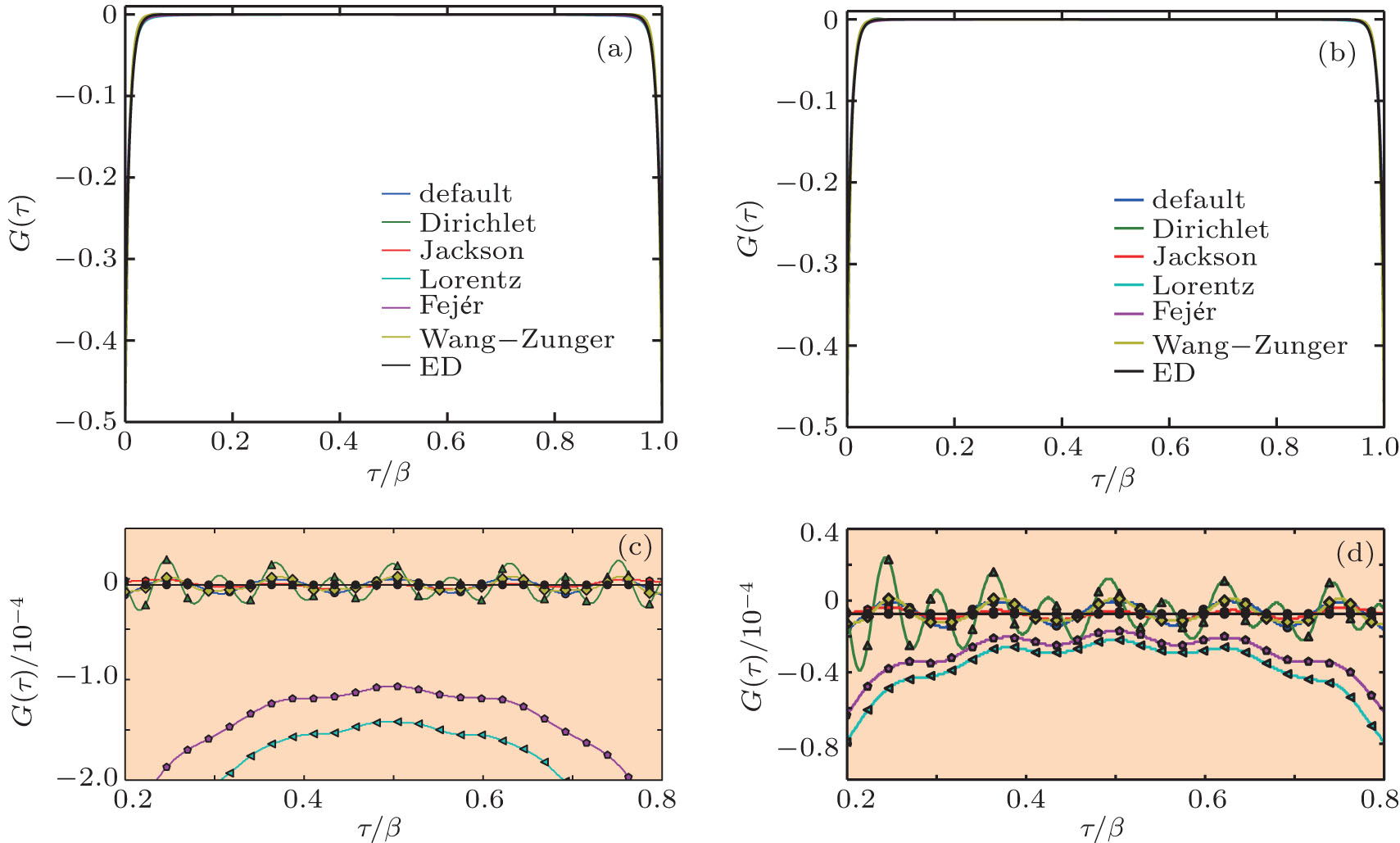
The imaginary-time Green’s function G(τ) of the single-band half-filled Hubbard model. The Coulomb interaction strength U is 6.0 and β = 50. (a) G(τ) calculated by Legendre polynomials with or without integral kernel functions. (b) G(τ) calculated by Chebyshev polynomials with or without integral kernel functions. In panels (c) and (d), the fine structures of G(τ) in τ ∈ [0.2β, 0.8β] interval are shown. They are obtained by Legendre polynomials and Chebyshev polynomials, respectively. The maximum order for the polynomial expansion series, n_max, is 96. The ED data are used for comparison. All data in panels (c) and (d) are magnified by a factor of 10000 for a clear view.