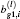† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11174274, 11174279, 61205021, 11204299, 61475152, and 61405194) and the State Key Laboratory of Applied Optics, Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences.
Multi-conjugation adaptive optics (MCAOs) have been investigated and used in the large aperture optical telescopes for high-resolution imaging with large field of view (FOV). The atmospheric tomographic phase reconstruction and projection of three-dimensional turbulence volume onto wavefront correctors, such as deformable mirrors (DMs) or liquid crystal wavefront correctors (LCWCs), is a very important step in the data processing of an MCAO’s controller. In this paper, a method according to the wavefront reconstruction performance of MCAO is presented to evaluate the optimized configuration of multi laser guide stars (LGSs) and the reasonable conjugation heights of LCWCs. Analytical formulations are derived for the different configurations and are used to generate optimized parameters for MCAO. Several examples are given to demonstrate our LGSs configuration optimization method. Compared with traditional methods, our method has minimum wavefront tomographic error, which will be helpful to get higher imaging resolution at large FOV in MCAO.
Because of atmospheric random disturbances, the wavefront from a star will be distorted, which blurs the image captured by large aperture, ground-based optical telescopes. Adaptive optics (AOs)[1,2] technology can be used to restore the imaging resolution close to the telescope diffraction limit by compensating the aberration induced by atmospheric turbulence in real time. The AO system is now considered to be an essential setup of many new large aperture optical telescopes.[3,4] In traditional adaptive optics, the distortion is measured by a wavefront sensor (WFS) and corrected by a wavefront corrector (WFC), such as a deformable mirror (DM)[5] or liquid crystal wavefront corrector (LCWC),[6–13] conjugated to the telescope pupil.[14,15] Unfortunately, this approach only achieves a good imaging resolution within a limited field of view (FOV) smaller than the isoplanatic angle that is generally only a few arc-seconds at visible wavelengths. Anisoplanatism leads to a limited FOV, which is a bottleneck of many applications of AO systems. To enlarge the FOV, multi-conjugate AO[16,17] has been developed by using several natural guide stars (NGS) or laser guide stars (LGS) in different directions. In a multi-conjugation adaptive optics (MCAOs) system, such as GeMS,[18,19] every guide star is sensed by an independent WFS, and several WFCs are conjugated to turbulence layers at different heights.
The atmospheric tomographic phase reconstruction and projecting three-dimensional turbulence phase onto WFCs are a necessary and very important calculation step for MCAO, which has been investigated by many groups.[20–24] These groups have discussed the influence of the number of mirrors and LGSs, but did not consider optimizing the specific location of LGSs and WFCs further. In these reported works, LGSs were simply located at the vertices of inscribed regular polygon inside the FOV, and the WFCs were placed at a position conjugated to the weighted mean height. Although Fusco proposed a method to optimize the NGS separation for a given FOV in Ref. [25], the distribution of NGS is not controllable, unlike the LGS that can be controlled by laser beam launch telescope. Up to now, LGS distribution and reasonable WFC conjugation altitude have not been optimized, though they are very important to obtain a high accuracy of atmospheric tomography. To resolve this problem and improve system imaging resolution at large FOV for MCAO, we have presented a new method to optimize the LGSs’ configuration and LCWCs’ conjugation heights. Our method is based on evaluating the field-averaged mean-square residual phase error variance of MCAO across the whole FOV for arbitrary configuration of LGS and LCWC analytically based on Zernike modes. The error variance is decomposed into reconstruction error related to LGS and correction error related to LCWC. Then, on one hand, by minimizing the wavefront reconstruction error averaged over the FOV, we get the optimal LGS configuration. On the other hand, we get the optimal conjugate altitudes of LCWCs by minimizing the error of wavefront correction for the MCAO system. After the optimization of the location of LGSs and LCWCs, we can obtain a phase reconstruction and compensation with high precisions, which is of great significance for multi-LGS AO system design.
In Section 2.1, Zernike coefficients representation for MCAO are given. Using a modal decomposition of the phase onto the Zernike polynomials basis, a simple analytical solution is proposed. The equations of shape of LCWCs and correspondent performance of MCAO are derived in Section 2.2. In Section 2.3, we also derive formulas for the computation of the covariance matrices based on the statistical property of atmosphere turbulence. In Section 3, a demonstration of multi-LGS optimization process is given and discussed. Finally, our conclusions are given in Section 4.
Modal decomposition of wavefront phase using Zernike polynomials is widely used in theoretical studies of AO. For a unit circular aperture without obstruction, the Noll Zernike modes are defined as follows:[26]

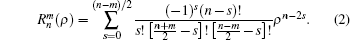
Figure
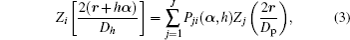

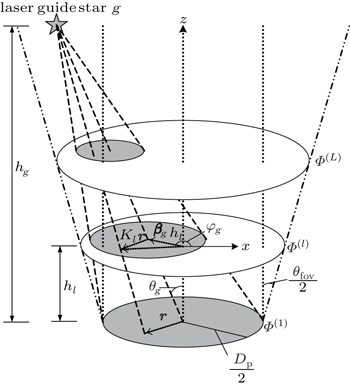
It is reasonable to assume that atmospheric turbulence aberration can be optically separated into L layers in different heights hl (l = 1,2,…,L)



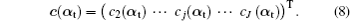
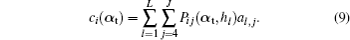

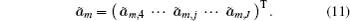

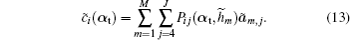
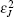
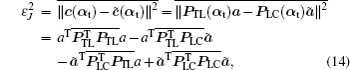
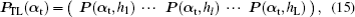
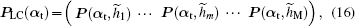

This section will discuss how to compute the instantaneous shape of LCWCs that are specified as the coefficients of wavefront expansion on Zernike modes. In Fig.
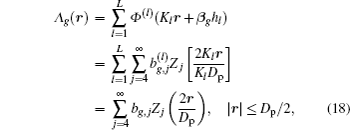
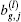
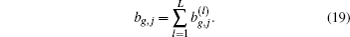
The number of wavefront reconstruction Zernike modes for WFS is limited by its number of sub-apertures. It is assumed that the highest order of WFS is equal to that of LCWC. Hence, the detection signal including all LGSs is

We neglect the temporal aspects of the MCAO operation by supposing that all measurements and corrections are done instantaneously. The computation of the optimal mirror shapes involves two sub-problems: atmospheric reconstruction and the derivation of the optimal mirror shape. We converge the two steps at a control matrix

The optimal modal wave-front compensation has a minimization of the statistical expectation of 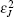


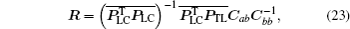
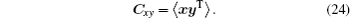
Putting Eqs. (




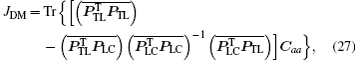
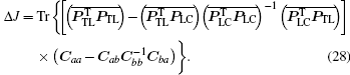
The computation of the covariance matrices
According to Eq. (
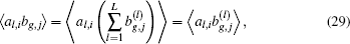


These covariances can be computed by a priori information on turbulence and the geometry of the LGSs of AO systems. Whiteley et al. introduced a generalized analysis geometry and used this aperture-and-source geometry with conventional methods to get a general expression for the inter-aperture cross correlation of the Zernike coefficients.[31] Assuming each turbulence layer’s statistics follows a von Kármán power spectral density with outer scale L0 and ignoring inner scale, we can get the following formula:


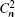
The aperture and source geometry for single-layer turbulence is shown in Fig.
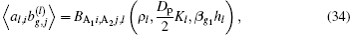

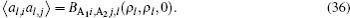
For this work, the well-known Hufnagel–Valley 5/7 model is used to describe the 
| Table 1. Four-layer turbulence model altitudes and relative layer strength. . |
We consider an 8-m telescope with several sodium LGSs (hg = 90 km). The LGSs are positioned in a circle of radius θg. In this paper, we focus our work on the optimization of configuration of LGS and conjugated heights of LCWCs. For simplification, the fitting error (variance of modes higer than J) and noise modeling are not considered here. Hence, we consider low-order correcting Zernike mode numbers 4-136 (radial order 15) without noise. For our atmospheric model, the uncorrected variance of those modes is 142.5 rad2.
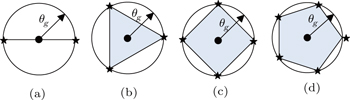
We compute the reconstruction error of different LGS constellations. The number of LGSs is in the range from 2 to 5. All LGSs are located at the vertices of regular polygons as shown in Fig.
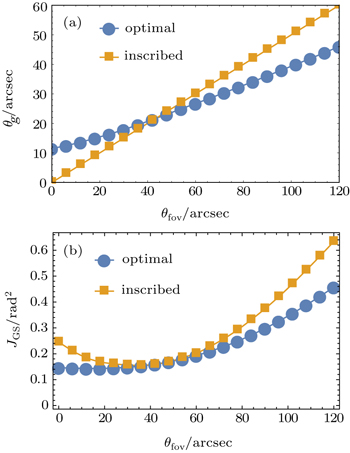
The result is shown in Fig.
 | Fig. 5. JGS as a function of θg. Gray dashed line at 30 arcsec is the inscribed θg. Results shown are for hg = 90 km, θfov = 1 arcmin, Dp = 8 m. |
| Table 2. The optimal θg and corresponding minimum JGS. . |
As shown in Fig.
Considering the cost and complexity of MCAOS, one generally uses several LCWCs in MCAOS. Here, in our simulation, we use three LCWCs in our simulation with one LCWC conjugated to the ground turbulence layer at 0 km as shown in Fig.
 | Fig. 7. Optimization of LCWCs’ conjugation heights. (a) Scheme of three LCWCs and their conjugated heights. (b) The optimal result of LCWC for 1-arcmin FOV. |
Figure
Based on the results and discussion above, we use the optimal parameters as listed in Table
| Table 3. Parameters for MCAO. . |
The average SR will be 0.6 and 0.58 in the FOV. The two MCAOS both have good performance at most region of FOV. The SR varies in the observed target direction
In this paper, a Zernike polynomial-based modal method was introduced to predict the higher-order error of MCAO across the field for arbitrary configuration of LGS and LCWC analytically. Then we obtained a phase reconstruction and compensation with high precisions by optimizing the location of LGSs and LCWCs conjugation heights. A demonstration of multi-LGS optimization process was given and discussed. We concluded that the optimal θg is linear to θfov and the optimal conjugated height of LCWCs is not affected by the FOV. Theoretical results indicated that our method would get the minimum wavefront reconstruction error for MCAO, and had higher imaging resolution at large FOVs. Additional experiments in our lab have been prepared to validate the method for the next-step research. Our method will benefit the design of MCAO in large aperture telescopes.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 |