Cite this Article
Zhou Zicong, Joós Béla. Effect of a force-free end on the mechanical property of a biopolymer — A path integral approach. Chinese Physics B, 2016, 25(8): 088701  
Permissions
Effect of a force-free end on the mechanical property of a biopolymer — A path integral approach
Zhou Zicong1, †, , Joós Béla2
Department of Physics, Tamkang University, Taiwan, China
Ottawa Carleton Institute for Physics, University of Ottawa Campus, Ottawa, Ontario, Canada, K1N-6N5

 

† Corresponding author. E-mail: zzhou@mail.tku.edu.tw

Project supported by the MOST and the NSERC (Canada).

Abstract
Abstract

We study the effect of a force-free end on the mechanical property of a stretched biopolymer. The system can be divided into two parts. The first part consists of the segment counted from the fixed point (i.e., the origin) to the forced point in the biopolymer, with arclength Lf. The second part consists of the segment counted from the forced point to the force-free end with arclength ΔL. We apply the path integral technique to find the relationship between these two parts. At finite temperature and without any constraint at the end, we show exactly that if we focus on the quantities related to the first part, then we can ignore the second part completely. Monte Carlo simulation confirms this conclusion. In contrast, the effect for the quantities related to the second part is dependent on what we want to observe. A force-free end has little effect on the relative extension, but it affects seriously the value of the end-to-end distance if ΔL is comparable to Lf.

PACS: 87.10.Pq;36.20.Ey;87.15.A−;87.10.−e
Keyword:statistical physics;path integral;biopolymers;mechanical property
1. Introduction

The conformational and mechanical properties of biopolymers have attracted considerable attentions owing to their importance in understanding the structure and function of biological materials.[1–29] In continuous elastic theory, a biopolymer is often modeled as a filament. The study of a filament has a long history dating back to Euler and Lagrange, and it has an increasing importance because it can be used to described the property of many microscopic objects such as biopolymers.[1–24,28] The simplest model for a biopolymer is the freely jointed chain (FJC) model and it is used to account for the conformational and mechanical properties of a flexible biopolymer. Another example is that the wormlike chain (WLC) model, which views the biopolymer as an inextensible chain with a uniform bending rigidity, has been used successfully to describe the entropic elasticity of a double-stranded DNA (dsDNA) or a semiflexible biopolymer.[1,4,5] Furthermore, the wormlike rod chain (WLRC) model, which is obtained by adding to the WLC model a term related to the intrinsic twist, has been used to explain the supercoiling property of dsDNA.[4,5,8] Owing to the importance of biopolymers, recently there has been a lot of works on the WLC and WLRC models as well as their modifications and extensions.

On the other hand, the path integral provides a powerful technique to study many physical phenomena. The basic idea of this technique can be traced back to Norbert Wiener, who introduced the Wiener integral to solve problems in the theory of diffusion and Brownian motion.[30] The complete method of the path integral was developed in 1948 by Richard Feynman,[31] with the original motivation to obtain a quantum mechanical formulation for the Wheeler–Feynman absorber theory. Since then, the path integral method has been applied widely to different areas in theoretical physics, including quantum field theory, solid state physics, statistical physics, polymer physics, and biophysics.[30–33] It has proved to be especially useful to describe the collective excitations in the theory of critical phenomena. This method often gives a simple way to obtain an exact solution for some physical problems. It also usually provides a solid foundation for the result obtained from other methods, to clarify the limits of their applicability and to indicate the way of finding corrections. For some realistic problems which are not exactly solvable, the path integral technique can help to build up a qualitative picture of the corresponding phenomenon and to develop some approximate methods of calculation.

For a time evolution system, the path integral is an analytic continuation of a method for summing up all possible trajectories of a moving body. It replaces the classical notion of a single, unique trajectory of a system with a sum over infinite possible trajectories to compute an amplitude or propagator. It is straightforward to see that a special configuration of a filament or a chain can be mapped into a trajectory of a moving body, with a replacement of the arclength of the filament by the time of the moving body. Therefore, it is straightforward to generalize the path integral technique to study the conformational and mechanical properties of a filament or a biopolymer.[4,10–12,14,16,21–23,30,32]

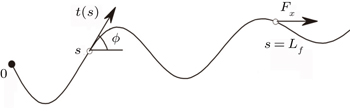
Traditional studies on the mechanical property of a filament usually assume that the external force or torque is applied exactly at one end of the filament. However, it is not easy to realize such a condition in a microscopic system so in practice the force is applied away from the end leaving a segment with a force-free end. Therefore, to have a complete understanding of the mechanical property of a microscopic filament, it is necessary to clarify the role of such a force-free end. In this paper we apply the path integral technique to answer this question.

The paper is organized as follows. In Section 2 we set up the two-dimensional (2D) model. Section 3 presents the results for the ground state. Section 4 makes a brief discussion in the configuration average. In Section 5 we present the results for the effect of the force-free end at finite temperature. Section 6 gives a brief discussion in the three-dimensional (3D) system. Finally, we end the paper with conclusions and discussions.

2. Two-dimensional model

Many observations on semiflexible biopolymers are conducted in a 2D environment so that the property of biopolymers in 2D has attracted growing interest.[3,13,15–17,19,21,23,28] It is also relatively easier to find some exact results in a 2D system.[21,28] Therefore, we begin from a 2D system.

In two dimensions, the configuration of a filament is determined by a vector, t ≡ dr/ds = {cosϕ, sinϕ}, which is tangent to the contour line of the filament, where r = (x, y) is the locus of the filament, s is the arclength, and ϕ(s) is the angle between the x axis and t, as shown in Fig. 1.

Fig. 1. Schematic diagrams of a curved filament showing the notation used.

Applying a uniaxial force (along the x axis) Fx at s = Lf, we can write the reduced elastic energy of a filament as[17,19,21,23,28]

where E is the energy, T is the temperature, kB is the Boltzmann constant, k is the bending rigidity, L is the total arc length of the filament and is a constant in the model so that the filament is inextensible, and f ≡ Fx/kBT. is the signed curvature and can be either positive or negative, and so does for c̃(s). c̃(s) is the intrinsic curvature. c̃(s) ≠ 0 means that, when Fx = 0, the ground-state configuration (GSC, or the spontaneous configuration, i.e., the configuration with the lowest energy) of the filament is a curve of curvature c̃(s). When c̃(s) = 0, it reduces to the WLC model. When k = 0, it becomes the FJC model.

3. Ground state configuration

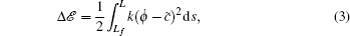
Extremizing E, we obtain the shape equation and boundary conditions (BCs) that govern the configuration of a filament in the ground state,

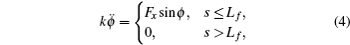
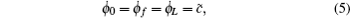
where ϕ0 = ϕ(0), ϕf = ϕ(Lf), and ϕL = ϕ(L). Equation (5) gives hinged BC or free BC, i.e., ϕ0, ϕf, and ϕL are not fixed. We do not consider other forms of BC since we focus on a filament at finite temperature in this paper.

It is clear that when s ≥ Lf, ϕ(s) = ϕf + c̃s. Moreover, the equation with s ≤ Lf is exactly the same as that of a filament with L = Lf. The filament with L = Lf has been studied in detail and it is found exactly that at T = 0 and when c̃ ≠ 0, x(L) undergoes a multiple-step discontinuous transition with increasing force[21,28] for a long filament, i.e., when L ≫ 2π/c̃, regardless of k.

4. Configurational average

In statistical mechanics, at finite temperature a static macroscopic quantity B̄ is defined as the average with Boltzmann weight over all possible conformations. For a continuous system, the average becomes a path integral in the form[4,10–12,14,16,21–23,30–33]

where is a ϕ-independent normalization constant. p0(ϕ0) and pL(ϕL) are distributions of ϕ0 and ϕL, respectively. p0 and pL are specified by the BCs. For instance, if we fix ϕ0 as ϕ0 or ϕL as ϕL, then p0 = δ(ϕ0 − ϕ0) or pL = δ(ϕL − ϕL). If ϕ0 or ϕL is free, then p0 =constant or pL =constant. There are some other kinds of BC, such as a hard wall[32] somewhere or forming a loop. In practice, with fixed or free BCs, we can ignore the corresponding p0 or pL in Eq. (6), and it is also the most often seen form of the mean in the literature,[4,10–12,14,16,21–23] especially for the time evolution system. In this convention, we should note that fixing ϕ0 or ϕL means that we do not integrate over ϕ0 or ϕL in Eq. (6). In contrast, free ϕ0 or ϕL means that it is necessary to integrate over ϕ0 or ϕL in Eq. (6). Physically, p0 and pL represent some constraints, similar to the constraint of a constant volume in the microscopic or macroscopic ensemble in statistical physics. These constraints are in general ignored in the literature so may result in some confusion.

In the realistic calculations, we can always arrange B[{ϕ(s)}] properly so that we can write it as B[ϕ,ϕn, …, ϕ1, ϕ0; s,sn, …, s1, s0] with L ≥ s ≥ sn ⋯ ≥ s1 ≥ s0, where ϕ ≡ ϕ(s), ϕk = ϕ(sk), k = 0,…,n. For instance, the end-to-end distance can be written as

so that inside the square bracket s and s1 are ordered. Therefore, for convenient in later derivations, we define a distribution function, P(ϕ,s;ϕ′,s′) with s ≥ s′, as

where ϕ′ = ϕ(s′) and C, which comes from Zk, is independent of ϕ and ϕ′ (but is dependent on BCs), then B̄ can be rewritten as

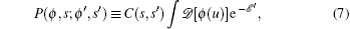
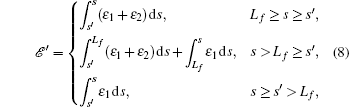
Note that if C is dependent on ϕ or ϕ′, then equation (10) is invalid.

From Eq. (1) we can see that, when f ≠ 0, ℰ is not an invariant with respect to a translation of ϕ, so that P cannot be in the form P(ϕ − ϕ′, s − s′). We can also show this conclusion using the series expansion method.[23] It follows that we cannot normalize P(ϕ,s;ϕ′,s′) directly since it results in a ϕ′-dependent C. With free ϕ0 and ϕL, P(ϕ,s;ϕ′,s′) represents the distribution of ϕ with a fixed ϕ′ because all P’s in Eq. (10) play the same role. But even in this sense, to normalize P is still meaningless. Moreover, note that BCs can affect the distribution at an arbitrary s, so that if ϕ0 and ϕL are not free, then P(ϕ,s;ϕ′,s′) do not have the meaning of a distribution function.

When f = 0, the exact distribution function, P(ϕ,s;ϕ′,s′) = P0(ϕ,s;ϕ′,s′) (s > s′), is found to be[23]

It is straightforward to show that (s ≥ s1 ≥ s′)

In this sense, P0 is also referred to as a propagator. In quantum mechanics, a propagator always satisfies such a relation. But we should point out that such an expression may be invalid for an arbitrary P(ϕ,s;ϕ′,s′) in our system, because C in Eq. (7) must provide B̄ = 1 when B[{ϕ(s)}] = 1, but there is no way to show that it is consistent with Eq. (13) for the arbitrary P(ϕ,s;ϕ′,s′) when f ≠ 0. For instance, a simplest choice of C is to let Cn+3 ∝ Zk, but such a choice is clearly inconsistent with Eq. (13). This should be a very important difference between quantum mechanics description and statistical mechanics description of the path integral method, but the relevant discussion seems unavailable in the literature.

5. Effect of a force-free end at finite temperature
5.1. With free ϕL

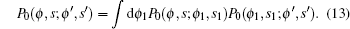
In experiment, usually ϕL is free so that we consider this case first.

5.1.1. When s ≤ Lf

In this case, using

we find exactly

Alternatively, we can use the standard path integral technique to discretize the functional integration in Eq. (6) first, and then integrate it term by term,[21] beginning from ϕL, to obtain the same result as in Eq. (14).

Equation (14) is exactly the same as that of the system with L = Lf, or it is equivalent to let Δℰ = 0. In other words, if we focus on the physical properties related to s ≤ Lf, then the force-free end does not have any effect. Note that this conclusion is valid even for a filament with s-dependent k and c̃, including the FJC model with k=0.

To check the conclusions obtained from the path integral method, we discretize the model and perform the Monte Carlo simulation method with the Metropolis algorithm to study it in the off-lattice system. For convenience, we only simulate the system with constant k and c̃. In the discrete model, the filament is consisted of N straight segments of length l0 and joined end by end. The coordinates of two ends of the i-th segment are therefore {xi−1, yi−1} and {xi, yi} with x0 = y0 = 0. The external force is applied at the Nf-th segment. Replacing 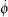by (ϕi+1 − ϕi)/l0, the reduced elastic energy becomes

where c ≡ c̃l0, κ ≡ k/l0kBT, F ≡ Fxl0/kBT. We also scale length by l0 so

and the relative extension is given by zN = 〈xNf〉/Nf. Therefore, F and zN are dimensionless quantities.

We have presented reports on the results with N = Nf (or L = Lf) for this model.[28] We found that if c ≠ 0 and at T > 0, zN undergoes a one-step first-order transition in the thermodynamical limit if the filament has a sufficiently large κ.

In this work we simulate the system with ΔN ≡ N − Nf > 0. We take c = 0, 0.1, 0.2, and 0.5 in this work. We set κ = 6 when c = 0 and 0.5; κ = 20 when c = 0.1; κ = 2 and 6 when c = 0.2. Nf = 50, 100, 200, and 300. ΔN = 2, 4, 6, 8, 10, 15, 20, 30, 40, and 50. The initial configurations are set randomly in this work. We equilibrate every sample for 106 Monte Carlo steps (MCS) before performing the averaging. The thermal average for a sample is taken to be 5 × 106 MCS. The MCS in this work are much less than that used in Ref. [28] since here we need only some qualitative results.

Some typical simulation results for zN are shown in Fig. 2. From Fig. 2, we can see that zN’s for the system with ΔN = 0 and ΔN > 0 are almost the same, so that these results support the conclusion that a force-free end indeed has no effect on the physical properties of a filament.

Fig. 2. zN versus F when κ = 6, c = 0.5 (black); κ = 2, c = 0.2 (red); and κ = 20, c = 0.1 (green). Nf = 300 in all cases. The lines (solid, dashed, dotted) are the systems with N = Nf and MCS = 3 × 108.[28] The black solid circle is for a filament with N = 315, the red empty-circle is for a filament with N = 320, and the green empty-square is for a filament with N = 310. MCS = 5 × 106 for circles and squares. Reduced units are used.
5.1.2. When s > Lf

In the same way as in the last section, when s > Lf, B̄ can be found in two steps

where s > sn > s′ > s+ > Lf > s−. g(ϕf,Lf) is dependent on ϕf and Lf, and is the same as the mean of the same quantity in a force-free system with an effective length ΔL = ΔN = L − Lf and a fixed initial angle ϕ0 = ϕf. Since P0 is well known, in many cases we can find a closed form for g(ϕf,Lf). For instance, for and constant k and c̃, using (this can be shown exactly using the standard path integral technique[21,23])

we obtain

where γf = c̃ΔL. When k = 0, i.e., for the FJC model, we obtain Δ xL = 0 as it should be. Equation (18) is in fact valid for all xs with s > Lf.

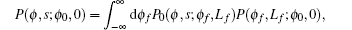
Replacing ΔL by L, 〈cosϕf〉 by cosϕ0, and 〈sinϕf〉 by sinϕ0, equation (18) recovers the xL of a force-free filament with a fixed ϕ0. This seems to be a trivial result, but we should note that exactly the behavior of Eq. (18) is different from that of the xL of a force-free filament with a fixed ϕ0. A typical example is that, with a free ϕ0, exactly 〈cosϕf〉 = 〈sinϕf〉 = 0 when f = 0 so that ΔxL = 0, regardless of k, L and c̃. But when ϕ0 is fixed, clearly ΔxL ≠ 0. This is because the two terms in the right-hand side of Eq. (19) are strongly correlated when ϕ0 is fixed since

In contrast, in general 〈cosϕf〉2 + 〈sinϕf〉2 varies with f and is not a constant, as shown in Fig. 3, so that knowing 〈cosϕf〉 does not mean knowing 〈sinϕf〉.

Fig. 3. 〈cosϕf〉2 + 〈sinϕf〉2 versus F for a filament when κ = 6, c = 0.5 (solid-circle); κ = 2, c = 0.2 (empty-circle); and κ = 20, c = 0.1 (solid-square). Nf = 300 in all cases. Reduced units are used.

From Eq. (18), it is clear that ΔxL/Lf → 0 when Lf→ ∞. Note further that ΔL appears in the form of e−ΔL/2k, we conclude that xL/L and xf/Lf should be almost indistinguishable in experiment. Therefore, for a long filament, the effect of the force-free end for the relative extension is negligible, regardless of ΔL.

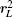
We can find similar results for some other quantities. Especially, replacing ΔL by L, we can show that is independent of ϕf, and is exactly the same as the of a force-free filament, which is basically dependent linearly on L.[21] In this case, if ΔL is comparable to Lf, then and will be quite different, so that one must be very careful to distinguish these two quantities in experiments.

5.2. With a Gaussian distribution on ϕL

Intuitively, it is very difficult to apply a constraint on ϕL without an associated force, except for binding some parts of a filament to form loops. Evaluating the effect of loops is a rather complex task so we will not discuss it in this work. For simplicity, we only present some expressions for a constraint in the form of a Gaussian distribution in ϕL, to demonstrate the complicated nature of the problem. Fixing ϕL can be regarded as taking α → ∞, so we do not consider it separately. In this case

Define

when s ≤ Lf, we can obtain

Again equation (23) is the same as that of the system with L = Lf, or it is equivalent to let Δℰ = 0 but with an effective Gaussian distribution, p(ϕf,Lf), for ϕf. But in this case we cannot say that the force-free end has no effect since p(ϕf,Lf) is dependent on both α and β.

Similarly, when s > Lf, we can find

Again, since P0 and p(ϕ,s) are well known, it is possible to find a closed form for some quantities with complex expressions.

6. On three-dimensional system

In the 3D case, the configuration of a filament can be described by a triad of unit vectors {ti(s)}i=1,2,3, where t3 ≡ dr(s)/ds is the tangent to the center line m (s) of the filament, and t1 and t2 are oriented along the principal axes of the cross section. The orientation of the triad as one moves along the filament is given by the solution of the generalized Frenet equations that describe the rotation of the triad vectors,[12,14]

where εijk is the antisymmetric tensor, and {ωi(s)} are the curvature and torsion parameters.

Applying a uniaxial force (along the z axis) Fz at s = Lf, we can write the reduced elastic energy of a filament with intrinsic curvatures ζ1(s), ζ2(s), intrinsic twist rates ζ3(s) and persistence lengths ai(s) as[12,14]

where θ(s) is the angle between the force and the z axis.

Again, a static macroscopic quantity B̄ is defined as a path integral

Similar to the 2D case, we can show exactly that when s ≤ Lf and with a free end at s = L,

Therefore, we find exactly the same conclusion as that in the 2D case, i.e., if we focus on the quantities with s ≤ Lf, then we can ignore the free end. Replacing the force by a torque, we can obtain the same conclusion. Moreover, for the quantities related to s > Lf, we can also find some results similar to that in 2D.

7. Conclusions and discussions

In summary, using the path integral technique, at finite temperature, we show exactly that for a filament if we focus on the quantities related to s ≤ Lf, then we can ignore the force-free end completely. In this paper we consider a uniaxial force only, but it is straightforward to generalize this conclusion to more general cases. In contrast, if we are interested in the quantities related to s > Lf, then the importance of a force-free end is quantity-dependence. A force-free end has little effect on the relative extension. But if ΔL is comparable to Lf, then a force-free end affects seriously the value of the end-to-end distance. Our conclusions are valid in both 2D and 3D, regardless of bending rigidity, intrinsic curvatures and intrinsic twist rates.

Reference
1Kratky OPorod G1949Recl. Trav. Chim. Pays-Bas681106
2Smith S BFinzi LBustamante C 1992 Science 258 1122
3Hernandez L IRamnarain S PHuff E JWang Y K 1993 Science 262 110
4Marko J FSiggia E D 1994 Science 265 506
5Bustamante CMarko J FSiggia E DSmith S 1994 Science 265 1599
6Cluzel PLebrun AHeller CLavery RViovy J LChatenay DCaron F 1996 Science 271 792
7Strick T RAllemand J FBensimon DBensimon ACroquette V 1996 Science 271 1835
8Fain BRudnick JÖstlund S 1997 Phys. Rev. 55 7364
9Moroz J DNelson P C 1997 Proc. Natl. Acad. Sci. USA 94 14418
10Nelson P C 1998 Phys. Rev. Lett. 80 5810
11Zhou HZhang YOu-Yang Z C 1999 Phys. Rev. Lett. 82 4560
12Panyukov S VRabin Y 2000 Phys. Rev. 62 7135
13Maier BSeifert URadler J O 2002 Europhys. Lett. 60 622
14Kessler D ARabin Y 2003 Phys. Rev. Lett. 90 024301
15Kulić I MMohrbach HThaokar RSchiessel H 2007 Phys. Rev. 75 011913
16Prasad AHori YKondev J 2005 Phys. Rev. 72 041918
17Vaillant CAudit BArnéodo A 2005 Phys. Rev. Lett. 95 068101
18Zhou ZLai P YJoós B 2005 Phys. Rev. 71 052801
19Moukhtar JFontaine EFaivre-Moskalenko CArnéodo A 2007 Phys. Rev. Lett. 98 178101
20Popov Y OTkachenko A V 2007 Phys. Rev. 76 021901
21Zhou Z 2007 Phys. Rev. 76 061913
22Zhou ZJoós B 2008 Phys. Rev. 77 061906
23Zhou ZJoós B 2009 Phys. Rev. 80 061911
24Ji CZhang L YHou X MDou S XWang P Y 2011 Chin. Phys. Lett. 28 068702
25Lei X LFang H PQi W P 2013 Chin. Phys. Lett. 30 128701
26Yao MQiu WLiu REfremov A KCong PSeddiki RPayre MLim C TLadoux BMege R MYan J2014Nat. Commun.54525
27Yao MGoult B TChen HCong PSheetz M PYan J2014Sci. Rep.44610
28Zhou ZLin F THung C YWu H YChen B H 2014 J. Phys. Soc. Jpn. 83 044802
29Lin F TChen B HZhou Z 2015 Chin. Phys. 24 028701
30Chaichian MDemichev A2001Path Integrals in Physics: Stochastic Process and Quantum MechanicsVol. 1BristolIOP Publishing Ltd
31Feynman R PHibbs A R1965Quantum Mechanics and Path IntegralsNew YorkMcGraw-Hill Book Company
32Wiegel F W1986Introduction to Path-Integral Methods in Physics and Polymer ScienceSingaporeWorld Scientific
33Kleinert H2009Path integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets5th edn.SingaporeWorld Scientific