† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11374100, 91536218, and 11274114) and the Natural Science Foundation of Shanghai Municipality, China (Grant No. 13ZR1412800).
We propose a novel scheme of optical confinement for atoms by using a concave grating reflector. The two-dimension grating structure with a concave surface shape exhibits strong focusing ability under radially polarized illumination. Especially, the light intensity at the focal point is about 100 times higher than that of the incident light. Such a focusing optical field reflected from the curved grating structure can provide a deep potential to trap cold atoms. We discuss the feasibility of the structure serving as an optical dipole trap. Our results are as follows. (i) Van der Waals attraction potential to the surface of the structure has a low effect on trapped atoms. (ii) The maximum trapping potential is ∼ 1.14 mK in the optical trap, which is high enough to trap cold 87Rb atoms from a standard magneto-optical trap with a temperature of 120 μK, and the maximum photon scattering rate is lower than 1/s. (iii) Such a microtrap array can also manipulate and control cold molecules, or microscopic particles.
In recent years, the grating has become a hot optical element in a wide range of applications such as filters,[1] vertical-cavity surface-emitting lasers,[2,3] high-efficiency photodetector,[4,5] and the grating magneto-optical trap.[6] Especially a kind of high-contrast grating (HCG) comprised of high-index grating completely surrounded by low-index materials, possesses extraordinary features: the ultra-broadband (Δλ/λ > 30%), high reflectivity (> 99%), and the ultra-high quality factor resonances.[7] Such striking optical features are attractive for various applications. A non-periodic flat grating reflector with focusing ability is first demonstrated.[8] An important property of flat HCG is that the wavefront phase of the reflected (or transmitted) light can be manipulated while maintaining a high reflectivity (or transmittance). With the precise adjustment of the structural parameters of HCG such as the grating period and filling factor, it is possible to create a parabolic wavefront phase and achieve an excellent focusing ability. Subsequently, the focusing performances for different kinds of flat grating reflectors have been extensively studied.[9–14] As is well known that when a two-level atom moves in an inhomogeneous light field, it will experience an optical dipole force and be attracted towards the maximum of the optical field.[15] Such a strong focusing optical field reflected from the flat (or curved) grating structure can provide the deep potential to trap the cold atoms, molecules and particles, so it would be interesting and worthwhile to design some controllable optical traps based on the grating metasurfaces and explore their potential applications in the fields of atom, molecule, and quantum optics. In this paper, a novel scheme of optical trapping for atoms by using a concave grating reflector is proposed and studied numerically. The grating reflector with the curved dielectric ring patterns not only obtains excellent focusing ability, but also can maintain high reflectivity. The favorable advantage of our scheme is that the light intensity reflected from the curved grating structure at the focal point is much higher than that from the flat one. Our study shows that such a focusing optical field can provide the deep potential to trap cold atoms.
We first present a resonant sub-wavelength grating structure that acts as a broadband reflector, which comprises a high-index material fully surrounded by a low index material, such as Si/air, depicted in Fig.
A reflector of one-dimensional flat grating structure has high reflectivity and a wide wavelength-tuning bandwidth, and it can be extended to two-dimensional (2D) grating structure with a concave surface shape. By locally tuning the filling factor, the reflection phase of the mirror is tailored to a parabolic distribution to the position while the reflectivity magnitude remains high everywhere, so that the reflector not only maintains a high reflectivity, but also obtains excellent focusing ability. We design a ring grating structure, namely, 2D concave dielectric-ring reflector, depicted in Fig.
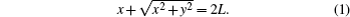
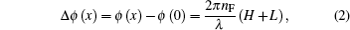
 | Fig. 2. (a) Schematic diagram of an HCG focusing dielectric-ring reflector. (b) Reflection phase-difference for focal length L = 10.5 μm. |
The spatial distribution of the optical field reflected by the ring-grating can be determined from Maxwell’s wave equation and simulated by using FEM software packages. In order to facilitate integrating an optical atom chip, at the bottom of the 11-ring grating structure with an upper diameter of 11 μm and a depth of 2.88 μm, we add a SiO2 substrate, shown in Fig.
 | Fig. 3. Schematic diagram of a three-dimensional (3D) optical focusing trapping with adding a SiO2 substrate under radially polarized illumination. |
Figures
We discuss the feasibility of the concave grating structure serving as an optical dipole trap.
When a neutral atom is placed into an optical field, it interacts with an electric field

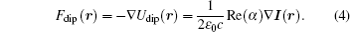
 | Fig. 5. (a) Potential depth along the y direction, and (b) the dipole force exerted on atoms in the laser field along the y direction. |
However, as the laser frequency is detuned further and further from resonance, owing to spontaneous scattering of the far red-detuned laser field, the heating should be considered as the dominant reason for atom loss from the atom trap. To quantify the effect, we should confirm the scattering rates. Hence, for Rb, the scattering rate, for an atom in a dipole trap is given as[15]

For the structure with a size of a few micrometers, when the trapped atom is near the dielectric surface, atom-solid state interaction becomes important. The Van der Waals potential may shift the trap minima. To quantify this effect, we use the Lennard-Jones (LJ) potential as an approximation,[19]
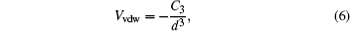

The 2D concave grating reflector not only has high reflectivity and a wide wavelength-tuning bandwidth, but also obtains excellent focusing ability. Figure
In addition, we also compare the focusing capability of our curved grating device with that of a perfect Si parabolic reflector, it is found that the perfect reflector can offer the same focusing performance, and its optical intensity at the focal point is enhanced by 40% compared with that of our curved grating reflector. For the fabrication of the perfect reflector with the parabolic smooth surface and micrometer size, it is harder than that of our curved grating structures proposed here. Our structures are processed by using electron-beam patterning followed by deep reactive-ion etching, which results in silicon pillars,[6,21] thereby showing that the curved grating reflector is an effective focusing device.
In this paper, we propose a novel scheme of strong optical confinement for cold atoms based on the concave grating structure. Our study shows that the grating reflector not only has high reflectivity and a wide wavelength-tuning bandwidth, but also exhibits high focusing ability. Under the incident polarized (1.55 μm) illumination, the grating reflector with a diameter of 15.2 μm can generate a focal spot with 10.5-μm focal length and 0.89-μm FWHM. In addition, such a focusing optical field reflected from the curved grating structure can provide the deep potential to trap the Rb cold atoms released from a standard magneto-optical trap with a temperature of 120 μK, and the maximum photon scattering rate in the optical trap is lower than 1/s. Our scheme can be used to construct various surface optical micro-structures to trap cold atoms. Such a microtrap array can also manipulate and control cold molecules, or microscopic particles such as dielectric spheres, metal particles, and living cells.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 |






