† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11534015 and 51371193).
We report on the magnetic and magnetoelectric properties of the Y-type hexaferrite BaSrZnMgFe12O22, which undergoes transitions from a collinear ferrimagnetic phase to a proper screw phase at 310 K and to a longitudinal conical phase at 45 K. Magnetic and electric measurements revealed that the magnetic structure with spiral spin order can be modified by applying a magnetic field, resulting in magnetically controllable electric polarization.It was observed that BaSrZnMgFe12O22 exhibits an anomalous magnetoelectric memory effect: the ferroelectric state can be partially recovered from the paraelectric phase with collinear spin structure by reducing magnetic field at 20 K. We ascribe this memory effect to the pinning of multiferroic domain walls, where spin chirality and structure are preserved even in the nonpolar collinear spin state.
In the past decade, there has been a revival of research on multiferroics materials in which magnetic and ferroelectric orders coexist.[1–5] The discovery of large magnetoelectric (ME) effect in TbMnO3[6] triggered numerous studies of multiferroics showing helical spin orders and led to the discovery of other new spiral multiferroics such as Ni3V2O8,[7] MnWO4,[8] and CoCr2O4.[9] These spiral multiferroics, which exhibit an inherent interplay between magnetic ordering and ferroelectricity, show pronounced ME effects, remarkable changes in electric polarization in response to a magnetic field. The microscope mechanism has been well explained by the spin current model[10] and inverse Dzyaloshinskii–Moriya model.[11] However, the operating temperatures of these multiferroics are too low (below 40 K) to be useful in practical applications.
Recently, some hexaferrites have been found to show magnetically induced electric polarization (P).[12–21] In 2005, it was first found that a Zn2Y-type hexaferrite Ba0.5Sr1.5Zn2Fe12O22 shows an relatively high ordering temperature of about 320 K for a proper-screw phase and magnet-field-induced ferroelectricity around 1 T.[12] It was then reported that the critical magnetic field to control spin helix and P became fairly low (1 mT–10 mT) in Mg2Y-type[13] and Al-doped Zn2Y-type[14] hexaferrites, resulting in sensitive ME responses and large ME effects. Subsequently, Co2Z-type hexaferrites were found to show low-field ME effect at room temperature.[16] Shortly afterwards, low-magnetic-field control of electric polarization were successively observed in M-type,[15] U-type,[18] W-type,[22] and Co2Y-type hexaferrites,[23] and most of them can operate at or near room temperature. Moreover, Co2Y-type,[23] Co2Z-type,[24] Al doping Zn2Y-type,[25] and CoZnY-type[26] hexaferrites also show inverse ME effect (electrical control of magnetization) at room temperature, representing a big step towards technical device applications.
In this paper, we demonstrate a magnetoelectric memory effect in a Y-type hexaferrite BaSrZnMgFe12O22 polycrystalline sample. This material possesses a relatively high spiral magnetic transition temperature of 310 K, below which successive metamagnetic transitions driven by magnetic field and resultant magnetically controllable ferroelectricity were observed. Since the ferroelectric polarization of BaSrZnMgFe12O22 arises from noncollinear spiral spin structures, the information of ferroelectric domains should be lost in the collinear spin phase. However, an anomalous magnetoelectric memory effect for the direction of electric polarization was observed after poling the sample to the nonpolar ferrimagnetic phase. We ascribe this phenomenon to the pinning effect of magnetic/ferroelectric domain walls by defects and space charge.
In experiment, polycrystalline samples with the composition of BaSrZnMgFe12O22 were synthesized by conventional solid-state reaction. Stoichiometric proportions of BaCO3, SrCO3, ZnO, MgO, and Fe2O3 powders were thoroughly mixed and well ground. Then, the mixed powders were calcined at 940 °C for 10 hours in air. The resulting mixture were reground, pressed into pellets, and sintered at 1200 °C for 4 hours in air for two times. Powder x-ray diffraction indicated that the samples are single phase. The magnetic and dielectric properties were performed using a superconducting quantum interference device magnetometer (Quantum Design MPMS-XL). For the measurement of dielectric constant and ME current (IME), the electrodes were made with silver paste onto the opposite faces of the plate-shaped samples with the dimension of 6.2 mm × 5.54 mm × 0.8 mm. The dielectric response was recorded by a NF ZM2353 LCR meter with an excitation of 1 V. ME current IME was measured by using an electrometer (Keithley 6517B) and a superconducting magnet (Quantum Design PPMS) with a handmade sample holder. Electric polarization P was obtained by integrating IME with respect to time.
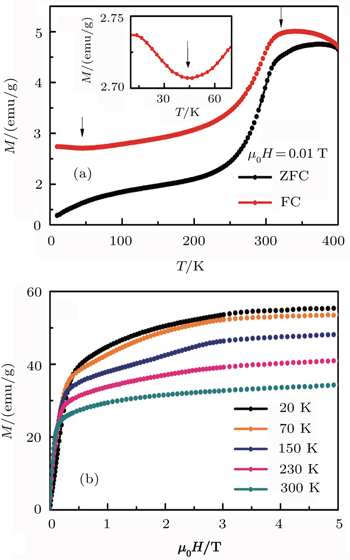
Figure
Figure
Even though the proper screw spin state of BaSrZnMgFe12O22 can sustain up to 310 K, the ME effect was measureable only below ∼ 100 K due to its low resistivity. Therefore, we show hereafter the low-temperature ME properties for BaSrZnMgFe12O22. Figures
 | Fig. 2. Temperature dependence of (a) magnetization, (b) dielectric constant, (c) ME current, and (d) electric polarization at 20 K. |
Figure
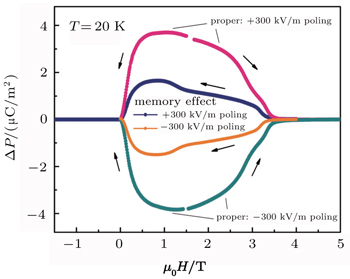
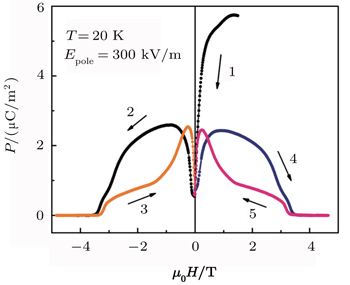
In order to verify whether the memory effect exists or not, following experiments with two kinds of poling procedures were carried out. The two sets of P–H data are shown in Fig.
If the sample was initially cooled down to 20 K under electric field (300 kV/m) and then poled the system in the proper ME poling process as stated above, the ME current could be detected with H sweeping from positive to negative. The electric polarization was integrated ME current by time. As shown in Fig.
In summary, BaSrZnMgFe12O22 possesses a relatively high spiral magnetic transition temperature (∼ 310 K), below which successive magnetic-field-driven metamagnetic transitions occur. Magnetoelectric measurements have shown that magnetic field can control electric polarization, related to evolution in magnetic structures. Because the sample is not insulating enough to sustain the ferroelectric polarization, ME effects can only be measured below ∼ 100 K. An anomalous magnetoelectric memory effect that the ferroelectric state can be partially reproduced from the paraelectric collinear spin phase by reducing magnetic field was observed. The frozen domain-wall motion is responsible to this memory effect. Furthermore, after electric-field cooling, magnetically controllable polarization can be preserved when magnetic field reverses, due to the pinning of multiferroic domain walls by defects and space charge.We expect that similar memory effects could happen in other multiferroic hexaferrites. Especially, in highly insulating hexaferrites with a high spiral transition temperature, one may observe the memory effect even at room temperature.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 |