Cite this Article
Huang Chang-Bao, Wu Hai-Xin, Ni You-Bao, Wang Zhen-You, Qi Ming, Zhang Chun-Li. First-principles calculation of the structural, electronic, elastic, and optical properties of sulfur-doping ε-GaSe crystal. Chinese Physics B, 2016, 25(8): 086201  
Permissions
First-principles calculation of the structural, electronic, elastic, and optical properties of sulfur-doping ε-GaSe crystal
Huang Chang-Bao, Wu Hai-Xin†, , Ni You-Bao, Wang Zhen-You, Qi Ming, Zhang Chun-Li
Anhui Provincial Key Laboratory of Photonic Devices and Materials, Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Hefei 230031, China

 

† Corresponding author. E-mail: hxwu@aiofm.ac.cn

Project supported by the National Natural Science Foundation of China (Grant No. 51202250).

Abstract
Abstract

The structural, electronic, mechanical properties, and frequency-dependent refractive indexes of GaSe1–xSx (x = 0, 0.25, and 1) are studied by using the first-principles pseudopotential method within density functional theory. The calculated results demonstrate the relationships between intralayer structure and elastic modulus in GaSe1–xSx (x = 0, 0.25, and 1). Doping of ε-GaSe with S strengthens the Ga–X bonds and increases its elastic moduli of C11 and C66. Born effective charge analysis provides an explanation for the modification of cleavage properties about the doping of ε-GaSe with S. The calculated results of band gaps suggest that the distance between intralayer atom and substitution of SSe, rather than interlayer force, is a key factor influencing the electronic exciton energy of the layer semiconductor. The calculated refractive indexes indicate that the doping of ε-GaSe with S reduces its refractive index and increases its birefringence.

PACS: 62.20.de;71.15.Mb;71.20.Nr;78.20.Fm
Keyword:S-doping GaSe;first-principles;linear response;mechanical properties
1. Introduction

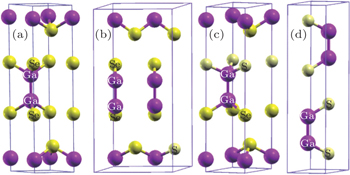
The layer ε-GaSe crystal, which belongs to space group is known as a typical member of III–VI semiconductors. Its multi-layer is composed of a four-sheet Se–Ga–Ga–Se intralayer stacking pattern. The intralayer bonds are ionic-covalent components, while interlayer bonds are of van der Waals type. The strong covalent bonding within the multi-layer and weak van der Waals bonding between the multi-layers make ε-GaSe a quasi-two-dimensional, highly anisotropic material with a birefringence of about 0.35 in the infrared range.[1] Combining its other excellent performances, such as large nonlinear coefficient (54 pm/V at 10.6 μm), wide transparency range (0.62 μm–18 μm) and high damage threshold, ε-GaSe have been successfully used to generate coherent laser radiation in an extremely wide spectral range from mid- to far-infrared[2–5] and further to terahertz regions[6–8] by nonlinear frequency conversion. On the other hand, the layer structure of ε-GaSe results in its pronounced cleavability and almost zero hardness; its bad mechanical properties lead to uncontrolled layer stacking defects (an admixture of γ, δ or β polytypes) in the growth process and hamper the cutting and polishing along arbitrary directions, which holds back its out-of-lab applications in nonlinear optics.

It was experimentally proved by many researchers that incorporation of different doping elements can significantly modify its mechanical and optical properties for frequency conversion. It is noted that In-doping[9,10] and Er-doping[11,12] ε-GaSe lead to 35% and 24% increase respectively in the intrinsic nonlinearity. Doping of ε-GaSe with Ag (0.04 mass%)[13] resulted in 10%–20% improvement in damage threshold and strengthened its hardness from 8 kg/mm2 to ≥ 10.7 kg/mm2, but 6% decrease in nonlinearity. Doping of ε-GaSe with Al (0.14 at%)[14,15] resulted in improved hardness up to 17 kg·mm–2 and increase of its ordinary refractive index. Te-doping[16,17] ε-GaSe resulted in 20% increase of nonlinearity and demonstrated the potential of frequency conversion into the THz range. In spite of the nonlinearity decreasing, S-doping[15,17,18] ε-GaSe resulted in 2.4 times and 1.5 times more efficient than pure and In-doping ε-GaSe crystal respectively due to its improvements of optical and mechanical properties. It was believed that the improvements of optical and mechanical properties in doping ε-GaSe were due to the modification of its cleavage property and decrease of stacking defects.

Despite the considerable amount of experimental work, there is relatively little research of the theoretical studies of doping ε-GaSe. In fact, the elastic and electronic properties of pure ε-GaSe have been investigated by using the full potential linear augmented plane-wave (FP-LAPW)[19,20] method, plane-wave pseudopotential (PW-PP)[21] method, and tight-binding (TB)[22] approach. It was suggested that the interlayer interactions were not solely of the van der Waals type in these layer compounds. Rybkovskiy and Arutyunyan[23] demonstrated the size-induced effects in ε-GaSe electronic structure by using pseudopotential method and GW approach. Further research was carried out by Rak et al.[24–27] to investigate the formation energies and electronic structures of In and Te defects in ε-GaSe, as well as the In-doping dependences of structural and mechanical properties. They pointed out that interstitial doping of cation-In can provide much higher energy barrier than those of the impurity of InGa and pure ε-GaSe as cleaving ε-GaSe crystal. However, there is a lack of theoretical approach to the electronic and mechanical properties of S-doping ε-GaSe. The present research focuses on the changes in electronic and mechanical properties caused by S-doping in ε-GaSe crystal.

2. Computational details

Our calculations were performed by using plane-wave pseudopotential method of density functional theory (DFT) as implemented in the ABINIT code.[28] The exchange-correlation energy of electrons was evaluated in the local-density approximation (LDA) within the Perdew-Wang scheme.[29] The effective ionic potentials were approximated by Troullier–Martins[30] type of norm-conserving pseudopotentials (NCPPs) and the valence electrons included 4s and 4p states of Se and S as well as 4s, 4p, and 3d states of Ga. Since the spin–orbit effects are expected to be small for III–VI compounds,[21] we did not include spin–orbit interaction in our calculations.

The primitive cells of ε-GaSe and β-GaS are schematically shown in Figs. 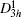1(a) and 1(d) respectively. Both ε-GaSe and β-GaS have the same laminar structure with each multi-layer containing four covalently joined atoms in the order X–Ga–Ga–X (X = S, Se) along the c axis. Different stacking arrangements of layers lead to different polytypes named ε (space group ) and β (space group ). It was noted that higher levels (0 < x < 0.4) of sulfur-dopant exist in GaSe1–xSx solution without changing its phase structure.[18,31] Thus, we consider the configurations with S atom located at the position of Se atom with x = 0.125 (Fig. 1(b)) and 0.25 (Fig. 1(c)) corresponding to GaSe0.875S0.125 and GaSe0.75S0.25 respectively. Unlike the experimental data, the sulfur-dopants with x = 0.125 and 0.25 would change symmetry of ε-GaSe crystal, from hexagonal system to monoclinic system. Therefore, the symmetry of Brillouin zone (BZ), elastic module and Born effective charge tensor would be changed. The calculated results are presented in Section 3.

Structural optimizations of GaSe1–xSx (x = 0, 0.125, 0.25, and 1) were carried out by two steps. The first step is to optimize the ionic positions without cell shape and size optimization, and the second step is to optimize the cell shape and size from the cell with relaxed ionic positions. The theoretical structures of GaSe1–xSx (x = 0, 0.25, and 1) were obtained by using small unit cells (8 atoms/cell) where the Brillouin zone was sampled by 10 × 10 × 2 mesh. For GaSe0.875S0.125 crystal, the calculations were performed on 2 × 1 × 1 supercell with the BZ sampled by a 6 × 12 × 3 grid of k points. Convergence tests indicated that these sets of k-points with energy-cutoff equal to 54 Ha (1 Ha = 2 Ry = 27.2114 eV) give an accuracy of about 0.001 Å for lattice constants.

Fig. 1. Schematic views of the crystal structure of (a) ε-GaSe, (b) GaSe0.875S0.125, (c) GaSe0.75S0.25, (d) β-GaS. The unit cells of ε-GaSe and β-GaS contain the same multi-layer structure and have different space group structures ( and respectively).

Linear-response properties such as the elastic module and Born effective charge (BEC) are obtained as second-order derivatives of the total energy with respect to external electric field or atomic displacements. Calculations of elastic modulus, dielectric functions and BEC were performed via the density functional perturbation theory (DFPT),[32–34] with a 60-Ha plane wave cutoff energy and Monkhorst–Pack grid equivalent to 12 × 12 × 4 grid on a primitive 8-atom GaSe1–xSx (x = 0, 0.25, and 1) cell. These sets of k-point energy cutoff can guarantee the adequate convergence of the calculations.

3. Results and discussion
3.1. Theoretical crystal structures

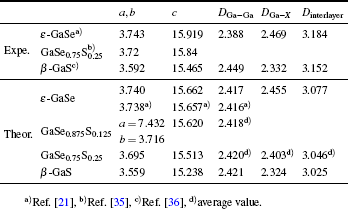
The calculated lattice parameters of GaSe1–xSx are listed in Table 1, along with previous theoretical and experimental data. According to previous studies, LDA is more specifically suited to describe the properties of III–VI layered materials, while generalized gradient approximation (GGA) excessively overestimates their experimental lattice parameters c and interlayer distances.[26] Our calculated lattice constants of ε-GaSe and β-GaS by LDA are about 1.5% smaller than the experimental values while the underestimations of interlayer distances are within 0.8% of the experimental values. These calculated results agree quite well with other theoretical results, and the underestimation of lattice parameter may be due to the well-known over-binding effect of LDA. The temperature factor may also make its contribution, because the calculations in this study are under the condition of 0 K compared with the experiments at about 300 K. Considering the thermal expansion effects, these optimized structures are more reasonable. For the frame of GaSe1–xSx (x = 0, 0.125, 0.25, 1) materials, their lattice constants monotonically decrease as the value of impurity concentration x increases. The compositional dependences of the lattice constants a and c are consistent with the variation trend of experimental results.[31]

Table 1.

The experimental and theoretical lattice parameters of GaSe1–xSx (x = 0, 0.125, 0.25, and 1). DGa–Ga, DGa–X, and Dinterlayer refer to the distances of Ga–Ga, Ga–X (X = Se, S) bond and interlayer. Unit is Å.

.

Since the electronic and elastic properties are sensitive to the inter-atomic distance of the semiconductor, we compare the distances of Ga–Ga (DGa–Ga) and Ga–X (DGa–X) of GaSe1–xSx (x = 0, 0.125, 0.25, and 1), as well as their interlayer distances (Dinterlayer). From ε-GaSe to β-GaS, we observe a decrease in the DGa–X and an increase in the DGa–Ga. This is because the S-atom is smaller than Se-atom and the ability for S atom to attract electrons is stronger than that for Se-atom, which could shorten the distance between S and Ga and lead to the decrease of DGa–X and the increase of DGa–Ga. With S incorporating into ε-GaSe, for GaSe0.875S0.125 and GaSe0.75S0.25, the above structural parameters are different between the multi-layer with SSe and multi-layer without SSe. As seen in Table 1, the S-doping reduces the DGa–X and increases the DGa–Ga in both layers. The average values of DGa–Ga, DGa–X and Dinterlayer are located between these of ε-GaSe and these of β-GaS.

3.2. Electronic properties

The electronic properties of ε-GaSe are calculated by using TB approach, PW-PP method and FP-LAPW method, as well as GW approximation. As pointed out in Ref. [26], the top of the valance band is derived from Se 4p electronic states. The effect of Ga 4s and Se 4p hybridization splits into two Se 4p derived bands near the top, giving rise to an energy gap in the band structure of ε-GaSe. Therefore, the electronic structure and band gap are sensitive to inter-atomic distance in this layer structure. Since different approaches give different results of lattice parameters and band gaps, we calculate the band structure of GaSe1–xSx crystals at optimized structural parameters obtained in LDA. In addition, we investigate the influence of interlayer distances on band gap of ε-GaSe.

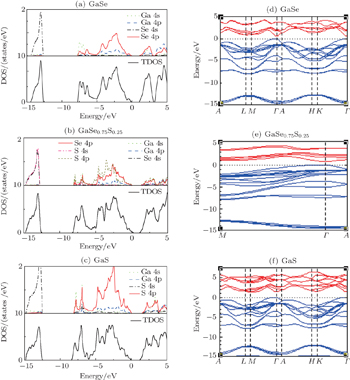
In order to characterize the substitutional impurity states, the densities of state (DOSs) of GaSe1–xSx (x = 0, 0.25, and 1) are calculated. The DOSs of these three materials look very similar. Their valence bands could be divided into three regions. It is seen in Fig. 2 that the bands in the deepest energy region (below –12 eV) are mainly contributed by X (X = S, Se) 4s electronic states. The bands in the intermediate energy region (located between –8 eV to –5.5 eV) are derived from the high contribution of Ga 4s states strongly mixed with X (X = S, Se) 4p states. The top valence bands originate from the X (X = S, Se) 4p slightly hybridized with Ga 4p. The low-lying conduction bands mainly consist of Ga 4s states of deep levels and X (X = S, Se) 4p states. The overlapping of electronic states indicates the characteristics of covalent bonds in GaX (X = S, Se). The main difference between ε-GaSe and β-GaS is the distributions of Se 4p states and S 4p states. Compared with Se-4p states of ε-GaSe, the S 4p states have much more contributions to total DOS of β-GaS in the top valence region, as well in GaSe0.75S0.25. The impurity of SSe in ε-GaSe may influence the electronic state and strength of chemical bond.

To investigate the influences of S-doping on the band gaps of GaSe1–xSx, we calculate the electronic band structures of GaSe1–xSx (x = 0, 0.125, 0.25, and 1). As mentioned above, ε-GaSe and β-GaS belong to the hexagonal system, while GaSe0.875S0.125 and GaSe0.75S0.25 belong to the monoclinic system. The orbital character of β-GaS is similar to that of ε-GaSe which has been described by Rak et al.[26] Due to the hybridization between the Ga 4s states and X (X = S, Se) 4p states, some of the X 4p bands are pushed up in energy, giving rise to the semiconducting gaps. However, the bottom of the conduction band in β-GaS is shifted to the M point compared with that in ε-GaSe: it is converted from a direct gap semiconductor into an indirect gap semiconductor. For GaSe0.75S0.25, the isovalent S-doping does not change the numbers of atoms and electrons per unit cell, so the number of valence bands is the same as those of ε-GaSe and β-GaS. Its band structure along Γ–A–M path is also similar to that of ε-GaSe. The calculated result shows that both the top of the valence band and the bottom of the conduction band lie at the Γ point, indicating that GaSe0.75S0.25 is a direct band gap semiconductor. In the calculation of GaSe0.875S0.125, we use the 2 × 1 × 1 supercell, and the results show that the size of BZ is reduced by half, while the number of valence bands is increased by double. GaSe0.875S0.125 in LDA calculation is also a direct band gap semiconductor. The calculated band gaps of GaSe1–xSx (x = 0, 0.125, 0.25, and 1) in LDA correspond respectively to 0.67 eV, 0.72 eV, 0.78 eV, and 1.40 eV (Table 2), which underestimates the band gap of GaSe1–xSx due to the well-known limitation of LDA. However, the calculated results are in accordance with the measured trend, indicating that the band gaps of GaSe1–xSx increase with the composition x increasing.

Fig. 2. Total and partial density of states (left) and electronic band structure (right) of ε-GaSe, GaSe0.75S0.25, and β-GaS calculated by the DFT–LDA method. The zero of the energy scale is adjusted to the valence-band maximum.
Table 2.

Band gaps (in units of eV) of GaSe1–xSx (x = 0, 0.125, 0.25, and 1) from experiments and LDA calculations. The band gaps of GaSe1–xSx increase with the composition x increasing.

.

As pointed out in the analysis of DOS, the upper valence band edge is formed by Se 4p states, whereas the conduction band bottom is composed of Ga 4s states. Moreover, the optimized structures indicate that the lattice constants decrease with the composition x increasing. The decrease of lattice constant is accompanied by the decreasing of Ga–X (X = S, Se) bond length, which leads to the increasing of overlapping between Ga 4s states and Se 4p states. In order to investigate the influence of interlayer force on band gap, the calculations have been done by altering the interlayer distance without changing the relative position of intralayer atoms. Based on the optimized result of ε-GaSe (named structure 0), the interlayer distances are assumed to increase 0.02 Å (named structure 1) and reduce 0.02 Å (named structure 2) respectively. The calculated band gaps of both structure 1 and structure 2, located at the Γ-symmetry point, are direct with the same value of 0.67 eV which is equal to that of structure 0. As the structure parameter is based on the optimized result of GaSe0.75S0.25, the band gap is also direct with a value of 0.76 eV which is between that of ε-GaSe (0.67 eV) and that of GaSe0.75S0.25 (0.78 eV). However, with using the structure optimized result of ε-GaSe without including Ga 3d electrons, the calculated band gap is shifted to be indirect with a value of 1.013 eV. Apparently, the positions of intralayer atoms and impurity of SSe are the key factor for influencing the electronic exciton energy. Note that S-doping could change van der Waals force between layers and then influence the equilibrium energy of GaSe. Therefore, the changes of van der Waals force could influence the distance of intralayer atoms and then alter its band gap.

3.3. Elastic properties

Elastic constants represent the second derivatives of the energy density with respect to strain:

describing the mechanical hardness and stability of crystal. The hexagonal crystals are characterized by five independent elastic constants: C11, C12, C13, C33, and C44. Crystal symmetry causes the elastic tensor to be composed of some independent components. The S-doping lowers the symmetry of ε-GaSe, from hexagonal to monoclinic system, thus increases the number of independent elastic constants. To gain further insight into the effect of S-doping, the elastic constants of GaSe1–xSx (x = 0, 0.25, and 1) are calculated after optimization of their geometries. The calculated results indicate that the new components of elastic constants of GaSe0.75S0.25 are so small that they could be negligible. Therefore, we assume that the isovalent S-doping does not actually change the symmetry of elastic tensor in GaSe crystal. The calculated elastic constants are presented in Table 3, together with available experimental and theoretical data.

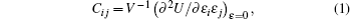
Table 3.

Calculated values of elastic constants (Cij), bulk modulus (B), shear modulus (G), Young’s modulus (E), and Poisson’s ratio (σ) for GaSe1–xSx (x = 0, 0.25 and 1) (unit is GPa for elastic constants and modulus).

.

The elastic constants C11 and C33 represent the resistances to longitudinal compression along the x and z crystallographic axes respectively, while C44 and C66 represent the resistances to transverse deformation in [100] and [001] crystal planes respectively. Therefore, the elastic constants of C11 and C66 are determined by the chemical bonds along [100] or [010] direction, while C33 and C44 are determined by the chemical bonds along [001] direction. For the GaSe1–xSx (x = 0, 0.25, 1) crystals, C11 is much higher than C33 and C66 is much higher than C44, suggesting that the bonding strength along the [100] or [010] direction is stronger than that along the [001] direction. These can be easily understood by the high anisotropy induced by the layer structure. From ε-GaSe to GaSe0.75Se0.25 to β-GaS, we observe monotonic increases in C11 and C66, but there is no obvious increasing nor decreasing trend in any of C33, C44, C12, and C13. These can be explained after a careful analysis of the relationships between the chemical bonds and elastic modulus of these layer compounds. The Ga–Ga bonds are along the z crystallographic axes and at about 120-degree angle with respect to Ga–X bonds (X = S, Se). The chemical bonds along [100] or [010] direction are composed of Ga–X bonds which determine the elastic constants of C11 and C66. The chemical bonds along the [001] direction are composed of Ga–Ga bonds and Ga–X bonds, and influenced by van der Waals force between layers. Therefore, the C33 and C44 are determined by the Ga–Ga bonds and Ga–X bonds, as well as interlayer force. As mentioned above, the Ga–S bond is shorter and stronger than Ga–Se bond, leading to the weakening of Ga–Ga bond from ε-GaSe to GaSe0.75Se0.25 to β-GaS. Thus, the doping of GaSe with S can increase its elastic constants of C11 and C66 and can change its C33 and C44.

From these calculated elastic constants, some important characteristics, such as bulk modulus B, shear modulus E, Young’s modulus EH and Poisson’s ratio σ, can be evaluated, and their results are also listed in Table 3. The bulk modulus (B) measures the resistance of material to volume change and provides an estimate of its response to hydrostatic pressure. The shear modulus G which is equal to the ratio of shear stress to shear strain is characteristic of the ability for a solid to resist transverse deformation. From ε-GaSe to GaSe0.75Se0.25 to β-GaS, our calculated bulk modulus and shear modulus are monotonically increasing: 30.2, 33.1, 36.1 for bulk modulus and 20.0, 20.9, 22.5 for shear modulus respectively. Moreover, the value of B/G empirically predicts the ductile and brittle behavior of material. The critical value that distinguishes brittleness from ductility is equal to 1.75. The values of B/G of ε-GaSe, GaSe0.75Se0.25, and β-GaS are 1.51, 1.58, and 1.60 respectively, suggesting these crystals are brittle. Young’s modulus which gives information about stiffness is estimated as the coefficient of proportionality at linear order between stress and strain. Our calculated Young’s moduli are also monotonically increasing: 49.2, 51.8, and 55.9, from ε-GaSe to GaSe0.75Se0.25 to β-GaS. Besides, Poisson’s ratio σ provides more information about the characteristics of the bonding forces than any of the other elastic constants. Poisson’s ratios are σ = 0.1 for covalent materials and σ = 0.25 for ionic materials, respectively. Our calculated values of Poisson’s ratio σ of ε-GaSe, GaSe0.75Se0.25 and β-GaS are 0.229, 0.239, and 0.242 respectively, suggesting that these crystals are ionic-covalent crystals and their iconicity values increase in the order from ε-GaSe to GaSe0.75Se0.25 to β-GaS.

Assuming the monotonic behavior for the mechanical properties of GaSe1–xSx to be a function of composition x value, doping of ε-GaSe with sulfur becomes stiff as the concentration of substitutional S increases. This can be explained by the changes of intralayer bonding induced by element-doping. However, it is experimentally observed that the doping of ε-GaSe with heavy atoms (like Te, In, and Er) can modify its cleavability and reduce its stacking defects. Although the C44 of S-doping crystals is larger than that of pure ε-GaSe, the increased effects from calculations are much smaller than experimental results. In the next subsection, we will try to search for different mechanisms and analyze the effects of Born effective charge on interlayer force.

3.4. Born effective charge analysis

The Born effective charge (BEC) tensor 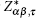is defined as the induced polarization of the solid along the Cartesian direction α by a unit displacement in the direction β generated by atom τ, under the condition of zero electric field. It is strongly influenced by dynamical change of orbital hybridization induced by the atomic displacement and can monitor the long-range Coulomb interaction responsible for the splitting between transverse and longitudinal optic phonon modes. For the laminar crystal of ε-GaSe, BEC tensor may be used for analyzing the intralayer bond strength and interlayer forces.

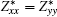
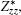
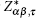
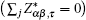
The BEC tensors of atoms in ε-GaSe and β-GaS each with hexagonal structure are diagonal and have only two independent components: along and perpendicular to the tetragonal axis, and respectively. Owing to BEC tensor being the same as the elastic tensor of GaSe0.75S0.25, the changes of BEC tensor induced by S-doping is negligible. The calculated eigenvalues of the symmetric part of are presented in Table 4, along with the average of eigenvalues. The charge neutrality sum rule is almost perfectly verified for each compound, suggesting that our results are well converged.

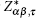
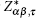
We observe that the tensors of Ga and X (X = Se, S) in each compound are strongly anisotropic. This fact indicates that the charge transfers along and perpendicular to the c axis are significantly different from each other. The average effective charges of Ga–ion and Se–ion in ε-GaSe are 1.78 eV and –1.78 eV respectively, and the average charges of Ga–ion and S–ion in β-GaS are 1.81 eV and –1.81 eV respectively. Compared with the nominal charges (Ga: + 2; Se, Se: –2), all of these are anomalously small, which indicates a strong covalent bond in the GaX (X = Se, S) layer structure. Since large corresponds to high ionicity, β-GaS has stronger ionic bonding than ε-GaSe. It is because the ability for S atoms to attract electrons is stronger than that for Se, which causes much more electrons to transfer from Ga–atom to S–atom. The stronger bonding force of Ga–S shortens its bond length compared to that of Ga–Se bond. The strengthening of Ga–X bond and the weakening of Ga–Ga may lead to the increases of C11 and C66 and decrease of C44 from ε-GaSe to β-GaS, which is consistent with the influence of lattice parameter on elastic modulus. As mentioned above, the doping of ε-GaSe with sulfur, for GaSe0.75S0.25, modifies its elastic modulus value between these of ε-GaSe and β-GaS except for C44.

Table 4.

Calculated Born effective charge tensors along with their average values for Ga, Se and S atoms in GaSe1–xSx (x = 0, 0.25, and 1).

.

Rak et al.[25] have investigated the formation energies of In-induced and Te-induced defects by first principles. Their calculations indicated that Te and In prefer the substitutional Se and Ga sites, respectively. Nevertheless, cation-In can also occupy interstitial site between multi-layers and form a chemical bond with anion–Se of adjacent multi-layers. They pointed out that it is this new bonding that strongly modifies the cleavability of the crystal along the plane parallel to the atomic layer. However, it is experimentally observed that not only the cation (In, Al, and Er) but also the anion (S, Te) can significantly modify the cleavage property of ε-GaSe and lower its stacking defects. We will explain this modification by analyzing BEC, which is shown in Table 4. Because of the high symmetry, all of the atoms in β-GaS structure have the same BEC values: 1.81 for Ga and –1.81 for S. For the ε-GaSe crystal with lower symmetry, its atoms have different BEC values between the two multi-layers and the charge neutrality sum rule is fulfilled in a unit cell and unfulfilled in a multi-layer (with a total value of 0.02 eV). The doping of ε-GaSe with S, for GaSe0.75S0.25, makes its BEC different from each other. The net charge is 0 in its unit cell and is 0.04 eV in a multi-layer. The van der Waals force between multi-layers includes instantaneous dispersion force, induction force and electrostatic interactions. The opposite net charge between neighbouring multi-layers produces the attractive electrostatic force and strengthens the resistance to transverse deformation in [100] (C44). Furthermore, substituting Se with S can influence the effective charge of atoms in the same multi-layers and neighbouring multi-layers. The non-uniform distribution of effective charge induced by the doping of S can increase the polarity of dipole and then interlayer induction force. The DFT fails to monitor the interactions of van der Waals force when calculating elastic response. Therefore, the increased C44 induced by S-doping from calculations is small compared with the experimental values. Note that the changes of crystal structure and ionic potential can influence the Hartree potential and exchange-correlation potential of electrons and thus its wavefunction and total energy. Our calculated C44 elastic moduli are 10.1, 10.8, and 11.2 for β-GaS, ε-GaSe, and GaSe0.75S0.25 respectively. We deduce that the modification of cleavability by S-doping derived from the increase of attractive electrostatic force and the improvement does not increase with the composition (x value) increasing. Moreover, the non-isomorphous incorporations of Ag, Er, Al may produce much more net charges and increase the interlayer electrostatic force of ε-GaSe. We suggest that the increase of attractive electrostatic force and interstitial defects of these cations mentioned by Rak et al.[25] are the source of the modification of its cleavability.

3.5. Refractive index

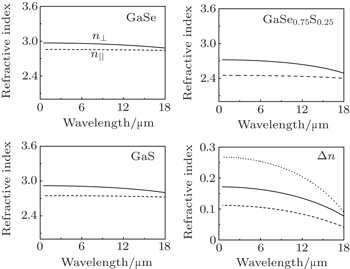
In order to investigate the effect of S-doping on refractive index of ε-GaSe, we calculate and compare the low-frequency dielectric permittivity tensors of infrared crystals: ε-GaSe, GaSe0.75S0.25, and β-GaS. The frequency dependent dielectric permittivity can be decomposed in the contributions of different modes as[32]

The first item εαβ (∞) on the right-hand side in Eq. (2) is high-frequency dielectric function which represents the electronic contribution to εαβ (ω). The second item represents the phonon oscillator contribution to εαβ (ω), where Sm,αβ is the mode oscillator strength tensor which is related to ionic displacements and Born effective charge tensors, ωm is the phonon eigen-frequency. The calculated high-frequency dielectric function εαβ (∞), along with previous experimental values, are listed in Table 5. Since the temperature and fault stacking of multi-layers can influence the dielectric function of ε-GaSe, the experimental values are different from each other. Our calculated results demonstrate that the high-frequency dielectric function εαβ (∞) decreases and the difference Δε increases from ε-GaSe to GaSe0.75S0.25 to β-GaS. Note that the underestimation of LDA usually leads to overestimation of dielectric function. In the transparent range, the refractive index of semiconductor (non-ferromagnetic material) is given as The frequency-dependent refractive indexes are shown in Fig. 3. The phonon effects make the dispersion curves slope downward. From ε-GaSe to GaSe0.75S0.25 to β-GaS, the refractive index is decreasing and the birefringence is increasing, indicating that the doping of ε-GaSe with S may lower its absorption coefficient. However, the increase of birefringence may worsen the walk-off effect in laser frequency conversion.

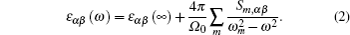
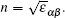
Table 5.

Calculated and experimental high-frequency dielectric tensor components ε‖ (parallel to the c axis) and ε⊥ (perpendicular to the c axis) of GaSe1–xSx (x = 0, 0.25, and 1).

.
Fig. 3. Refractive indexes of ε-GaSe, GaSe0.75S0.25, and β-GaS calculated by using the DFPT method. The phonon effects make the dispersion curves slope downward. From ε-GaSe to GaSe0.75S0.25 to β-GaS, the refractive index is decreasing and the birefringence is increasing.
4. Conclusions

In this paper, we present the results of first principles: lattice parameters, electronic structures, elastic moduli and birefringences of GaSe1–xSx (x = 0, 0.25, and 1). The relationships between intralayer structure and elastic modulus from ε-GaSe to GaSe0.75S0.25 to β-GaS are demonstrated. The calculated results indicate that the strengths of Ga–X (X = Se, S) bonds and elastic moduli of C11 and C66 increase with the increase of composition (x value) for GaSe1–xSx. The analysis of Born effective charge provides an explanation for the significant modification of cleavage properties for the doping of ε-GaSe.

We find that the distance between intralayer atoms and substitutions of SSe, rather than interlayer force, is a key factor of influencing the electronic exciton energy of the layer ε-GaSe semiconductor. However, the change of interlayer distance may influence the distance between intralayer atoms and further affect the band gap of ε-GaSe. From ε-GaSe to GaSe0.75S0.25 to β-GaS, the refractive index is decreasing and the birefringence is increasing, indicating that the doping of ε-GaSe with S may lower its absorption coefficient. However, the increase of birefringence may worsen the walk-off effect in laser frequency conversion.

Reference
1Allakhverdiev K RYetis M ÖOzbek S 2009 Laser Phys. 19 1092
2Eckhoff W CPutnam R SWang S X 1996 Appl. Phys. 63 437
3Ding Y JKhurgin J B 1998 J. Opt. Soc. Am. 15 1567
4Shi WDing Y JMu X 2002 Appl. Phys. Lett. 80 3889
5Imahoko TTakasago KSumiyoshi T 2007 Appl. Phys. 87 629
6Zhong KYao J 2010 Opt. Commun. 283 3520
7Rao ZWang XLu Y 2011 Opt. Commun. 284 5472
8Ding Y JShi W 2006 Laser Phys. 16 562
9Suhre D RSingh N BBalakrishna V 1997 Opt. Lett. 22 775
10Feng Z SKang Z H 2008 Opt. Express 16 9978
11Hsu Y KChen C WHuang J Y 2006 Opt. Express 14 5484
12Feng Z SGuo J 2014 Opt. Commun. 318 205
13Xie J JGuo J 2013 Opt. Commun. 287 145
14Guo JXie J J 2013 CrystEngComm 15 6323
15Das SGhosh CVoevodina O G2005Appl. Phys. B8243
16Ku S AChu W C 2012 Opt. Express 20 5029
17Kang Z HGuo J2012Appl. Phys. B108545
18Kokh K AMolloy J F 2015 Mater. Chem. Phys. 154 152
19Ghalouci LBenbahi BHiadsi S 2013 Comput. Mater. Sci. 67 73
20Zhang D WJin F TYuan J M 2006 Chin. Phys. Lett. 23 1876
21Kosobutsky A VSarkisov S YBrudnyi V N 2013 J. Phys. Chem. Solids 74 1240
22Camara M O DMauger ADevos I 2002 Phys. Rev. 65 125206
23Rybkovskiy D VArutyunyan N R 2011 Phys. Rev. 84 085314
24Rák ZMahanti S DMandal K C 2010 Solid State Commun. 150 1200
25Rak ZMahanti S DMandal K C 2010 Phys. Rev. 82 155203
26Rak ZMahanti S DMandal K C 2009 J. Phys. Chem. Solids 70 344
27Rak ZMahanti S DMandal K C 2009 J. Phys.: Condens. Matter 21 015504
28Payne M CTeter M PAllan D C J D 1992 Rev. Mod. Phys. 64 1045
29Perdew J PWang Y 1992 Phys. Rev. 45 13244
30Troullier NMartins J L 1991 Phys. Rev. 43 1993
31Ho C HWu C CCheng Z H 2005 J. Cryst. Growth 279 321
32Gonze XLee C 1997 Phys. Rev. 55 10355
33Veithen MGonze XGhosez P 2005 Phys. Rev. 71 125107
34Baroni SDe Gironcoli SDal Corso A 2001 Rev. Mod. Phys. 73 515
35Sasaki YNishina Y 1981 J. Phys. Soc. Jpn. 50 355
36Belenkii G LSalaev E YSuleimanov R A 1985 Solid State Commun. 53 967
37Scamarcio GCingolani ALugar‘a M 1989 Phys. Rev. 40 1783