† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61222501, 61335004, and 61505003), the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20111103110019), the Postdoctoral Science Foundation of Beijing Funded Project, China (Grant No. Q6002012201502), and the Science and Technology Research Project of Jiangxi Provincial Education Department, China (Grant No. GJJ150998).
A two-dimensional apodized grating coupler for interfacing between single-mode fiber and photonic circuit is demonstrated in order to bridge the mode gap between the grating coupler and optical fiber. The grating grooves of the grating couplers are realized by columns of fully etched nanostructures, which are utilized to digitally tailor the effective refractive index of each groove in order to obtain the Gaussian-like output diffractive mode and then enhance the coupling efficiency. Compared with that of the uniform grating coupler, the coupling efficiency of the apodized grating coupler is increased by 4.3% and 5.7%, respectively, for the nanoholes and nanorectangles as refractive index tunes layer.
Grating couplers, as one of the key elements enabling the light to be directly coupled between the planar waveguide circuits and the optical fibers, are widely used in the field of silicon photonic integrated circuits.[1–3] The coupling efficiency is limited by the scattering efficiency, the directionality and the mode matching degree between the exponential decline field of the upward diffracted field and the fundamental mode of the single-mode fiber (SMF).[4,5] The 100% scattering efficiency could be reached by designing a long enough grating that fulfills the Bragg condition at the target wavelength. The directionality can be avoided by using a metal mirror, or by optimizing the buried oxide (BOX) thickness through the interference effect inside the substrate layer.[6,7] By now, the main difficulty in further improving the coupling efficiency is the mode mismatch between the exponentially declined diffraction field and the Gaussian field of the SMF.[8] There is about 20% coupling efficiency loss caused by the mode mismatch. It is a challenge to bridging such a mode mismatch to further improve the coupling efficiency between the grating coupler and optical fiber. Many approaches have been proposed to increase the mode matching degree, such as the nonuniform etching depth of the grooves, nonuniform duty cycles by tuning the scattering efficiency of each groove.[8–10] However, the process is relatively complicated.
Recently, nanostructures have exhibited the feasibility of the effective refractive index tailoring according to the equivalent medium theory, which relaxes the refractive index limitation by the current bulk material.[11] Engineering the effective refractive index distribution of the gratings could modify the grating strength and then the profile of the diffraction light. Detailed design method for digitally apodized grating couplers with Gaussian diffractive mode has been published without considering any practical limitations.[12] With the back mirror, the calculated coupling efficiency of 93.1% at 1550 nm with 3-dB bandwidth of 82 nm can be achieved. The matching degree has reached 97.3% between the field profile of upward-diffracted light and optical fiber mode. However, the BOX thickness is 2.2 μm, which is unavailable commercially. Based on the equivalent medium theory, the two-section apodized subwavelength gratings were fabricated on a silicon-on-insulator (SOI) substrate. The calculated and measured peak coupling efficiency were 60.3% and 50.4% at about 1550 nm for TE mode, respectively.[13,14] Photonic crystal (PhC) structure was also employed to engineer the refractive index of each groove to improve the coupling efficiency.[15] The selection of the effective refractive index is determined by the hole size. The calculated and measured coupling efficiency of 66% and 67% for the TE mode were realized.[16] By bonding an aluminum mirror to employ the back reflection light, the coupling efficiency increased to about 87.5%.[17]
However, in practice, the width of the Gaussian mode is about 20 μm when the field intensity decreases to almost 0 according to the fitting of the Gaussian mode in the standard SMF with a full width (1/e) of 10.4 μm, which determines the total length of the grating. On the other side, suppression of the grating strength will increase the transmission loss for the commercial SOI substrate. Because the difference between the exponential decaying field and the Gaussian mode is large at the beginning of the grating, it is important to suppress the grating strength at the beginning. Figure
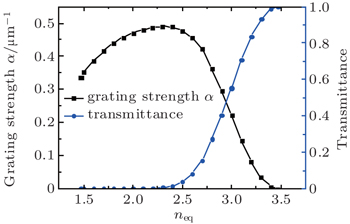 | Fig. 1. Calculated dependences of the grating strength and transmittance on the effective refractive index of grating grooves. |
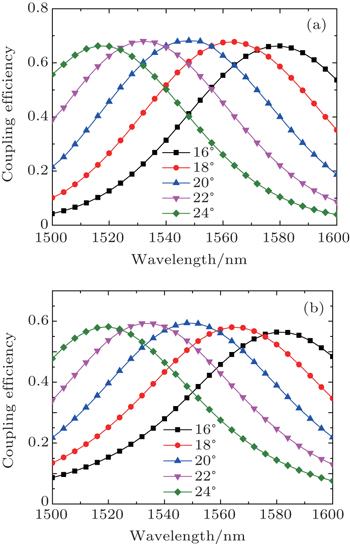
The apodized grating couplers using fully etched both nanorectangles and nanoholes were fabricated by considering the transmittance loss. The coupling efficiencies are increased by 5.7% and 4.3%, respectively, compared with those of the uniform grating couplers at 1550 nm. Compared with a traditional shallowly etched grating coupler, the proposed apodized fully etched grating coupler with grating grooves realized by columns of fully etched nanostructures has two advantages. One is that with the feasibility of digital tailoring, the effective refractive index of each groove can obtain the Gaussian-like output diffractive mode. The other is that the fully etched grating coupler can simplify the fabrication process since it can be fabricated by using the same process as that for fabricating the strip waveguide.
Figure
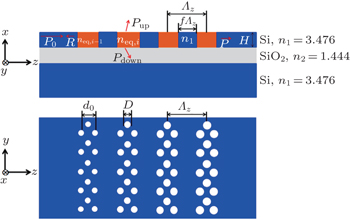 | Fig. 2. Schematic diagram of an apodized grating coupler with nanostructures serving as grating grooves: (a) side view; (b) top view. |
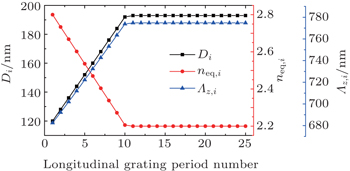
In order to obtain high coupling efficiency, the selection of the effective refractive index of each groove is determined by a large number of trials. Two-section grating couplers are determined with the first section as the effective refractive index linearly varies from 2.8 to 2.2 for the first 10 periods. The second section uses a uniform effective refractive index of 2.2 along 15 periods. The maximum effective refractive index is limited to 2.8 for the lower transmittance loss according to Fig.
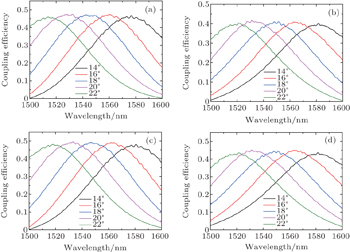
Figure
Figure
 | Fig. 6. SEM images of the fabricated apodized (a) and uniform (b) grating coupler with nanorectangles, apodized (c) and uniform (d) grating coupler with nanoholes. |
Figure
In this work, the apodized grating couplers by using nanorectangles and nanoholes to digitally tailor the effective refractive index of each groove are demonstrated, which is to bridge the mode gap between the grating coupler and optical fiber. The maximum coupling efficiency of 49.5% with 3-dB bandwidth of 69 nm is reached. Compared with that of the uniform grating couplers, the coupling efficiencies of the apodized grating couplers are increased by 4.3% and 5.7%, respectively, for the nanoholes and nanorectangles as refractive index tuning layer. The improved coupling efficiency benefits from the better mode matching between the grating couplers and SMF.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 |