† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11274242, 11474221, and 11574229), the Joint Fund of the National Natural Science Foundation of China and the China Academy of Engineering Physics (Grant No. U1330203), and the National Key Basic Research Special Foundation of China (Grant Nos. 2011CB922203 and 2013CB632701).
We propose a simple all-optical diode which is comprised of an asymmetric ring cavity containing a two-level atomic ensemble. Attributed to spatial symmetry breaking of the ring cavity, direction-dependent optical bistability is obtained in a classical bistable system. Therefore, a giant optical non-reciprocity is generated, which guarantees an all-optical diode with a high contrast up to 22 dB. Furthermore, its application as an all-optical logic AND gate is also discussed.
The optical diode is essential in optical computation and communication,[1–4] as well as in the quantum information processing area. Until now, kinds of non-reciprocal schemes have been fabricated, such as the magneto-optic[5–7] and acousto-optic effects systems,[8] the chiral structures,[9,10] nonlinear parity asymmetric systems,[11–14] etc. However, most of them were either active which need strong external electromagnetic field, or very complicated which need an accurate micro/nano-scale processing technique.
Recently, non-reciprocal light transport has been realized experimentally in a parity-time asymmetric system.[15,16] Parity-time symmetry can be broken by taking into account the gain saturation in an active resonator.[16] Although the coupled active-passive whispering-gallery microcavities can provide a non-reciprocal isolation ratio from −8 dB to +8 dB, high-Q resonator is needed and it is not passive. In this work, we will show a high contrast optical diode up to 22 dB in a pure passive system comprised of an asymmetric ring cavity containing a saturable absorptive atomic ensemble, which indicates that active medium, parity-time asymmetry and high-Q resonators are not always necessary.
In our previous work,[17,18] we have shown that the time-reversal asymmetry, spatial asymmetry and optical nonlinearity are three significant factors for optical non-reciprocity, which is consistent with the result of Ref. [19]. In the present work, we will show a giant non-reciprocity in a classical atomic gas-cavity coupling system, which easily fits these three factors. Specifically, optical nonlinearity naturally happens due to saturable absorption of gas, and spatial symmetry can be broken by furnishing different reflectivity walls, meanwhile time-reversal asymmetry is naturally satisfied by taking into account non-radiative dissipations of the cavity and the resonant absorption of atoms.
Although optical absorptive bistability was realized first in 1969,[20] and since then on, a great deal of attention has been paid to observing and understanding the phenomenon of optical bistability[21–24] in symmetric or one-side cavity, there was little work on controllable bistability within asymmetric cavity.[18,25] In our previous work,[18] we have presented a new proposal to obtain giant optical non-reciprocity up to 13 dB by using single-atom controllable bistability in an asymmetric cavity. We have shown that single-atom bistable states were controlled by the asymmetric walls of the cavity and it is feasible to realize the smallest all-optical diode. However, the manipulation of single atom in nano-cavity is still tough in a quantum optical system. It will be much convenient if we can realize this kind of optical diode in a classical optical bistable system.
In this work, we pay attention to the asymmetric ring cavity containing a two-level atomic ensemble which can be performed much more easily under the present technology. More interestingly, we also find an apparent direction-dependent bistability within the asymmetric ring cavity, which can be used to realize a much higher contrast optical diode up to 22 dB. Specifically, under a certain input power, it shall operate in the linear regime (Iin < Il) for the forward input case while it shall work in the saturated regime (Iin > Iu) for the backward input case. Here Iin, Il, and Iu are the input intensity, the lower, and upper threshold intensities of bistability regime, respectively.
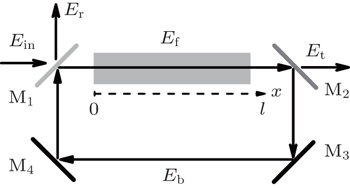
The model considered is shown in Fig.
Here, we distinguish the forward input case from the backward input case. The forward input case is shown in Fig.
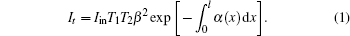

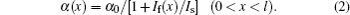
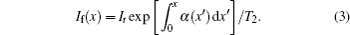
By using the iterative method we can solve Eqs. (
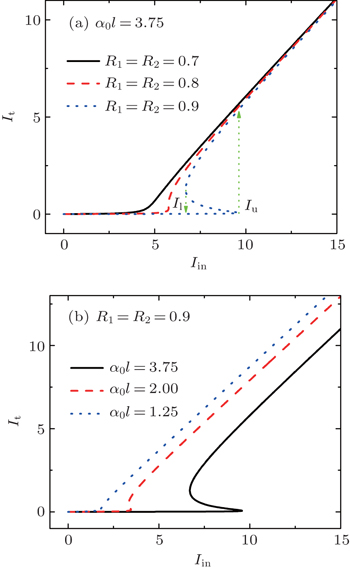
In order to check the availability of our method, we calculate the input-output relation for the case of symmetric cavity first, i.e., R1 = R2. By fixing the linear absorption coefficient as α0l = 3.75 which was presented in Ref. [20], the curves of It versus Iin are plotted in Fig.
Now we discuss the direction-dependent optical bistability induced by spatial symmetry breaking in the asymmetric ring cavity. The reflectivities of mirrors M1 and M2 are set to be R1 = 0.8 and R2 = 0.9 to present asymmetric ring cavity, respectively. By fixing α0l = 3.75, the relations between It and Iin for forward and backward input cases are plotted as the solid and dashed curves in Fig.
For the forward input case, input field is incident on M1 with R1 = 0.8 at first, and the solid curve in Fig.
The non-reciprocal transport in the present asymmetric system originates from the varying optical nonlinearities induced by absorption saturation in two input cases, which is similar to that in the active system.[16] More importantly, our scheme works in the bistable regime while the active system does not, which is the reason why our scheme can generate much higher transmission contrast than previous ones. In this work, the optical bistable regime is separated significantly between the forward and backward input cases. Therefore, our scheme will provide excellent optical non-reciprocity. Furthermore, our scheme is passive and without high-Q resonators.
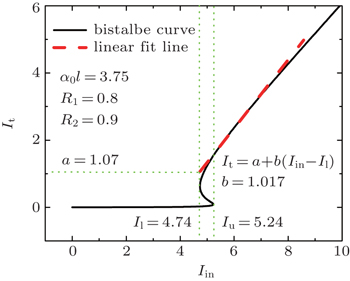
Here, we show how to construct an efficient optical diode under the optimal window of operation power. As shown in Fig.
To explain such a direction-dependent optical bistability and non-reciprocity analytically, we explore the bistability condition in detail. Since the value of αl is near zero undergoing large input power, the exponential term e−αl can be approximated by 1 − αl. Taking the forward input case for example, with the definition of X = Iin/(IsT2) and Y = It/(IsT2), the equation connecting the input power Iin and the transmitted power It can be simplified into

However, the threshold intensities Il and Iu are direction-dependent due to the definition X = Iin/(IsT2). For the case of forward input, Il (Iu) ∝ T2. Meanwhile for the case of backward input, Il (Iu) ∝ T1. In Fig.
The direction-dependent optical bistability can be used not only as optical diode or isolator, but also as optical switching, memory, transistor,[27] etc. Here we introduce a new application as optical logic AND gate. Despite the superiority of such a kind of logic gate, our proposal provides a new access to it at least. The block diagram of such a logic AND gate is shown in Fig.
Here, optical logic states 0 and 1 are characterized by the intensity of the field, which can be defined as
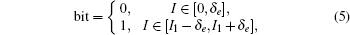
As is well known, the output power It in the saturated regime can be simplified into a linear function, i.e., It = a + b·(Iin − Il), where a and b are the fitting parameters. In principle, a and b as well as Il can be adjusted by the reflectivities of walls. Logic AND gate should fulfill the following conditions at least, i.e. δe < a/2 and I1 ∈ (Iu/2 + a/2, Il − a/2).
As an example, we set α0l = 3.75, R1 = 0.8, R2 = 0.9 and plot curve of It versus Iin in Fig.
| Table 1. Logical operations of AND gate. . |
Finally, we discuss the experimental proposal to such an optical diode and a logic AND gate. Since there are many bistable experiments done in symmetric classical macro cavity, we can retain their main equipment presented in Ref. [20] but only replace the symmetric cavity with the asymmetric ring cavity. However, the bistable operating power was rather high in the past work and it should be lowered to an acceptable level. As is well known, the saturable critical power Is ∝ 1/μ2τ,[20,28,29] where μ and τ are atomic dipole moment and the atomic lifetime of the saturable medium in the resonator, respectively. Thus larger μ and τ are beneficial to lower Is.[22] Recently, there were a remarkable series of experiments in bistable multiple-quantum-well devices that lowered the critical power to an acceptable level.[24,27] Since silicon-based optical micro devices are desired, we also present a possible experimental proposal based on micro/nano technology. Recently, on-chip whispering-gallery microcavities with gain and loss have been fabricated.[16] Therefore, it is not difficult to construct such a four-mirror ring cavity with loss in one of the rectangle sides after careful designing. Four Bragg reflectors[30] should be placed in the corners of ring cavity and the spatial asymmetry can be obtained by furnishing different Bragg reflectors. Therefore, it is feasible to realize such a kind of optical diode and logic AND gate.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 |