Cite this Article
Zhou Naigen, Liu Bo, Zhang Chi, Li Ke, Zhou Lang. Molecular dynamics study of anisotropic growth of silicon. Chinese Physics B, 2016, 25(7): 078109  
Permissions
Molecular dynamics study of anisotropic growth of silicon
Zhou Naigen1, Liu Bo1, Zhang Chi1, Li Ke1, Zhou Lang1, 2, †,
School of Materials Science and Engineering, Nanchang University, Nanchang 330031, China
Institute of Photovoltaics, Nanchang University, Nanchang 330031, China

 

† Corresponding author. E-mail: lzhou@ncu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 51361022, 51561022, and 61464007) and the Natural Science Foundation of Jiangxi Province, China (Grant No. 20151BAB206001).

Abstract
Abstract

Based on the Tersoff potential, molecular dynamics simulations have been performed to investigate the kinetic coefficients and growth velocities of Si (100), (110), (111), and (112) planes. The sequences of the kinetic coefficients and growth velocities are μ(100) > μ(110) > μ(112) > μ(111) and v(100) > v(110) > v(112) > v(111), respectively, which are not consistent with the sequences of the interface energies, interplanar spacings, and melting points of the four planes. However, they agree well with the sequences of the distributions and diffusion coefficients of the melting atoms near the solid–liquid interfaces. It indicates that the atomic distributions and diffusion coefficients affected by the crystal orientations determine the anisotropic growth of silicon. The formation of stacking fault structure will further decrease the growth velocity of the Si (111) plane.

PACS: 81.10.–h;81.10.Aj;87.10.Tf
Keyword:anisotropy growth;kinetic coefficient;silicon;molecular dynamics
1. Introduction

Multicrystalline silicon (mc-Si) solar cells have been occupying the mainstream photovoltaic market because of their low production cost[1] and high stability.[2] However, the conversion efficiency of mc-Si solar cells is lower than that of single crystalline silicon solar cells. In order to improve the conversion efficiency of mc-Si solar cells, the mc-Si ingot has experienced three typical development stages in industry: common mc-Si, mono-like silicon, and high efficiency mc-Si. They focus on the techniques of lowering the dislocations density, controlling the crystal orientations and the sizes of the grains in the mc-Si ingot,[3–6] respectively. Anisotropic growth plays an important role in all these techniques.

There is little experimental literature about the anisotropic growth of Si crystal owing to the difficulty in experiment. Fujiwura[7] studied the competitive growth of the (100) to (111) planes of Si by building a bicrystal artificially, and observed the anisotropic growth at a high undercooling temperature. They have also found different morphological transformations at different solid–liquid interfaces by in situ observation, and proposed equations for calculating the growth velocity of Si ⟨112⟩ and ⟨110⟩ dendrites.[8–10]

The anisotropic growth is also a fundamental issue for crystal growth from melt. It has been extensively studied in the field of metal solidification. The anisotropic growth of crystal is mainly described by the kinetic coefficient μ, a very important parameter describing the movement of the solid–liquid interface. Many results showed that the kinetic coefficients of different growth planes in FCC metals[11–15] obey μ(100) > μ(110) > μ(111). Various theories were put forward to explain the above relationship. The typical theories consider the difference of interface energy,[16–20] interplanar spacing,[21] and formation of stacking fault.[22] Although Apte and Zeng[16] have obtained the (100), (110), and (111) solid–liquid interface energies of silicon by molecular dynamics, there is little in the literature studying the kinetic coefficient μ of the different growth plane of Si. In this paper, we calculate the melting points of different planes in order to set the undercoolings for them, and then investigate the kinetic coefficients and the crystal growth velocities of the different planes. Finally, the atomic distribution and the diffusion coefficient of the atoms near the solid–liquid interface are investigated to explain the anisotropic growth of silicon. This paper is to supply a reference for improving the quality of mc-Si and the conversion efficiency.

2. Model and method
2.1. Molecular dynamics model of crystal growth and melting

Figure 1 shows the crystal growth and melting model. The disordered atoms at both ends of the model are cut from a pre-melting system at high temperature. The regular arranged atoms in the middle part of the model are the Si crystal, which represents a crystal nucleus during the process of crystal growth. As shown in Fig. 1, the orientations of the crystal nucleus along the X, Y, and Z axes are [100], [010], and [001] directions, respectively. The model represents the melting or growth of plane (100). The initial size of the crystal nucleus is 20a × 20a × 12a (a is the lattice constant). There are about 90000 crystal atoms and 50000 melting atoms in the initial model for the crystal growth along plane (100); there will be a slight difference of the number due to the different crystal structures of different planes. The orientation of the crystal nucleus will be subject to change to accommodate the simulation needs.

Fig. 1. Crystal melting and growth model of silicon (100) plane.

The inter-atomic forces are calculated with the Tersoff potential,[23] which has been shown to be appropriate for modeling the transition from melt to crystal of silicon.[24] The Tersoff potential based on the concept of bond order in quantum mechanics was brought by Tersoff in 1986, and has been revised twice in 1988 and 1989, forming three editions T1,[25] T2,[26] and T3.[23] The Tersoff potential can well describe the diamond structure and the non-positive body structure. The formulas of the T3 potential are shown as follows:

where fc is the interruptive function, Ri j is the cut-off radius, VR is the repulsive force from the nearest neighbor atoms, VA is the attractive force from the nearest neighbor atoms, and bi j is the bond order of atom i and atom j. Although the melting point of Si obtained with the Tersoff potential is higher than the experimental value, it does not matter because we focus on the difference between the temperature and the melting point, such as the cooling temperature.

Newton’s equations of motion are integrated with the velocity form of the Verlet algorithm using a time step of 0.001 ps. The simulation is performed in an NPT ensemble with periodic boundary conditions on three directions.

The Verlet algorithm[27] is the most commonly used algorithm in molecular dynamics. This algorithm is based on the third-order Taylor expansions for positions r(t), one backward and one forward,

Add these two expressions, and ignore the high order term, we have

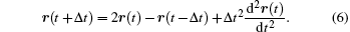
That is the basic expression of the Verlet algorithm.

2.2. Calculation of crystal growth velocity

The crystal growth velocity is calculated according to the variation of the number of crystal atoms (Nc).[28] To determine whether an atom belongs to the crystal or not, we calculate the number of its “neighbors”, which are the atoms within a sphere with a radius of the average distance of the first and the second nearest neighbor distances. If the number of neighbor atoms is equal to that of the first nearest neighbors in the corresponding perfect crystal, the atom at the center of the sphere is considered as a crystal atom, and vice versa. After adding up the crystal atoms in the system, the crystal growth or melting velocity can be calculated by the slope of the curve of crystal atom number versus time, and the formula is as follows:

where Nc is the crystal atom number, d0 is the atomic layer spacing, and N0 represents the number of atoms in each layer.

3. Results and discussion
3.1. Melting points of different crystal planes

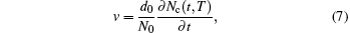
The melting point is the temperature at which melting or solidification of bulk materials occurs. The micro-process of melting always starts from the crystal defects in the surface, such as grain boundaries and dislocations. For a single crystal, the melting points of different planes should be different and will be a little higher than that of polycrystalline due to a lack of grain boundaries. We calculate the melting points of the Si (100), (110), (111), and (112) planes using the method of backward induction of melting velocity by molecular dynamics.[29] Firstly, the system is melted at different temperatures, and the melting velocities are calculated according to Eq. (7) based on the function of the number of crystal atoms with time. Then the melting velocity can be drawn in a figure as a function of temperature, as shown in Fig. 2.

Fig. 2. Crystal melting velocity of silicon (100) plane at reduced temperature.

We extrapolate the curve of the melting velocity to zero, i.e., the cross point with the temperature axis, which gives the melting point of that plane. The melting points of Si (100), (110), (111), and (112) planes are obtained. The descending order of them is (100), (110), (111), and (112) planes. Table 1 lists these values relative to that of the Si (112) plane. The melting points are different from plane to plane, but the maximum difference is only 24 K, which is not much of a difference. This result is similar to Sun’s research on Ni.[13]

Table 1.

Melting points of different planes of silicon. The value is relative to that of the (112) plane.

.
3.2. Kinetic coefficients

The kinetic coefficient is calculated by the free solidification method.[30] The simulations of the crystal growth along different planes have been performed at different undercoolings, which is set according to the melting point of each plane shown in Table 1. The crystal growth velocity at a given undercooling can be calculated according to Eq. (7). The results are shown in Fig. 3.

Fig. 3. Growth velocities of different planes of silicon at different undercoolings.

The crystal growth velocities increase linearly with the increase of undercooling for the (100), (110), and (112) planes, and almost linearly for the (111) plane. The slopes of the fitting lines, the kinetic coefficients, are different. The corresponding values are μ(100) = 0.031 m·s−1 · K−1, μ(110) = 0.029 m·s−1 · K−1, μ(112) = 0.028 m·s−1 · K−1, and μ(111) = 0.0050 m · s−1 · K−1. The sequence is μ(100) > μ(110) > μ(112) > μ(111), which is very similar to that of the FCC metal,[11–15,29,31] μ(100) > μ(110) > μ(111). There are few studies on the (112) plane in metal. Here we pay attention to this plane because the dislocations easily emerge along it.

3.3. Crystal growth velocities

Anisotropic growth of silicon at different temperatures has also been investigated. The reduced temperatures (relative to the melting point of the (112) plane) are set here as 0.81, 0.85, 0.89, 0.93, and 0.97, respectively. The growth velocities are calculated according to the variation of the number of crystal atoms as described in the previous section. The results are shown in Fig. 4. There are similar relationships between the growth velocities and the temperature for the four planes: the crystal growth velocities slowly rise at first and then decrease dramatically after passing through a maximum as the temperature increases. This variation is similar to that of metal platinum and silver.[12] While the four planes of silicon present different growth velocities at the same temperature. The sequence of the velocities at a temperature is v(100) > v(110) > v(112) > v(111), which is the same as that of the kinetic coefficients.

Fig. 4. Crystal growth velocities of different planes as a function of the temperature.
3.4. Discussion

The difference of interfacial energy,[16] interplanar spacing,[21] and the formation of stacking fault[23] are always used to interpret the anisotropic growth. Table 2 lists the relevant parameters of the different planes of silicon. The sequence of interfacial energy of these planes is γ(100) > γ(110) > γ(111). According to the principle of lowest energy, the sequence of the kinetic coefficients or the growth velocities should be (111) > (110) > (100). This is completely opposite to our results. The reason is that the interfacial energy interpretation is suitable for the growth of polycrystalline, where the plane with lower interfacial energy will dominate the growth because it can lower the whole interface energy. However, the interpretation of interfacial energy is unsuitable here, because the area of interface keeps almost constant during the process of crystal growth, and it cannot explain the difference of kinetic coefficients of different planes.

Table 2.

The relevant parameters of Si (100), (110), (112), and (111) planes.

.

The interplanar spacing interpretation comes from the BGJ growth model.[22] The main point of this model is that the growth is governed by the collisions of the melting atoms with the growth interface. If the time of growing one layer is close for each plane, the interplanar spacing will play an important role in the growth. A plane with wider interplanar spacing will grow faster. Several studies on metals[11–15,29,31] have shown great agreement with this theory. For example, Hoyt[11] found that the ratio μ(100)/μ(110) is approximately equal to the ratio of the interplanar spacings of the (100) and (110) planes. 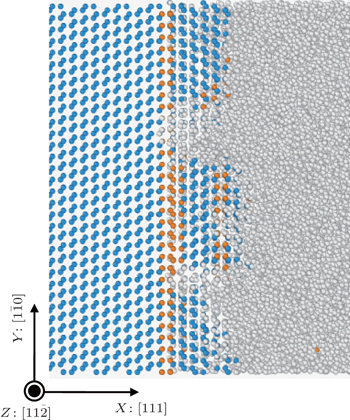As shown in Table 2, the order of the interplanar spacings of the four planes of silicon is not consistent with that of the kinetic coefficients. The reason may be that the difference of the interplanar spacings must lead to the difference of the plane densities due to the determinate bulk densities. The effect of the atomic density in a plane on growth will be much more than that of metal owing to the influence of the covalent bonds of Si.

We investigate the influence of the orientation on the structure and the atomic movement of Si melt. Figure 5 shows the functions of atomic layer density along different orientations during the crystal growth. As shown in Fig. 5, the functions of atomic layer density present regular peaks in the crystal nucleus part. Every peak represents one atomic plane, and the arrangement of the peaks of each orientation is different as the arrangement of the atomic planes. The functions of atomic layer density are flat in the melt far away from the crystal part and present one or more small peaks in the melt near the interfaces. The small peaks continue the arrangement of the peaks in the crystal. It indicates that the crystal orientation plays an important role in the distribution of the melt atoms near the interface. This result is similar to the ordering phenomenon of Al melting atoms.[32] It is interesting that the lengths of these fluctuations of the layer densities affected by the crystal orientation are different, and the order is the same as that of the kinetic coefficients.

Fig. 5. Layer densities along different orientations during the growth.

We further calculate the diffusion coefficients of the melting atoms near the solid–liquid interfaces at the reduced temperature of 0.99 by the MSD method.[33] The results are shown in Fig. 6. The diffusion coefficients of the melting atoms far away from the interfaces are kept constant for the four orientations. However, the diffusion coefficients of the melting atoms near the solid–liquid interfaces are obviously different for the four crystal orientations. From the interface to the middle of the melt, the diffusion coefficients gradually rise as the distance to the interface increases. The diffusion coefficients are different for the four crystal orientations at the same distance. The sequence of them is D(100) > D(110) > D(112) > D(111), which is the same as that of the kinetic coefficients. It indicates that the crystal orientations affect the distributions of the melt atoms near the solid–liquid interfaces, and then affect the diffusion coefficients of the atoms, which finally result in the anisotropic growth of the Si crystal.

Fig. 6. Diffusion coefficients near the solid–liquid interfaces at reduced temperature of 0.99.

The kinetic coefficient and diffusion coefficient of the Si (111) plane are much lower than those of the other three planes as shown in Figs. 3 and 6. There should be other special factors affecting the growth of the Si (111) plane. Figure 7 shows the projection of the atomic structure of the growth system along the Si (111) plane. A stacking fault structure can be observed clearly in the system. It may be the special factor lowering the growth velocity of the Si (111) plane. The (111) plane of the FCC structure holds two types of sites for the next plane: FCC sites (normal sites) and HCP sites (mistake sites), and they have a very small energy difference. During the crystal growth, the two sites compete to select melting atoms. The FCC sites prevail. Occasionally, the HCP sites succeed, and a stacking fault emerges. This competitive growth model will decrease the velocity of the crystal with the FCC structure, as reported for the FCC metal.[11–15] A little difference is that Si crystalline has two suits of FCC structures.

Fig. 7. The projection of the system growing along the (111) plane.
4. Conclusion

The relative melting point, kinetic coefficient, and growth velocity of Si (100), (110), (111), and (112) planes have been investigated by molecular dynamics. It is found that the melting points of the four planes are close. The melting points of Si (100), (110), (111) planes are 24 K, 15 K, and 13 K higher than that of the Si (112) plane, respectively. The sequences of the kinetic coefficients and the growth velocities are μ(100) > μ(110) > μ(112) > μ(111) and v(100) > v(110) > v(112) > v(111).

The analysis of the interface energy or interplanar spacing fails to interpret the anisotropic growth of Si, though it succeeds for metals. The distribution and diffusion coefficient of the melting atoms near the interface are affected by the crystal orientation. Their sequences agree well with the sequences of the kinetic coefficient and growth velocity, which can explain the anisotropic growth of Si. That is, the crystal orientations affect the distributions of the melt atoms near the solid–liquid interfaces, and then affect the diffusion coefficients of these atoms, which finally result in the anisotropic growth of the Si crystal.

The stacking fault structure can easily form due to the close-packed structure of the Si (111) plane. The forming of the stacking fault structure is a process of competitive growth between FCC sites and HCP sites, which will decrease the growth velocity of the Si (111) plane. It leads to the kinetic coefficient and growth velocity of Si (111) being much lower than those of the other three growth planes.

Reference
1Li J MChong MZhu J CLi Y JXu J DWang P DShang Z QYang Z KZhu R HCao X L 1992 Appl. Phys. Lett. 60 2240
2Sarti DEinhaus R 2002 Sol. Energy Mater. Sol. Cells 72 27
3Würzner SHelbig RFunke CMöller H J 2010 J. Appl. Phys. 108 083516
4Stokkan G 2010 Acta Mater. 58 3223
5Wang H YUsami Fujiwara KKutuskake Nakajima K 2009 Acta Mater. 57 3268
6Usami NYokoyama RTakahashi IKutsukake KFujiwara KNakajima K 2010 J. Appl. Phys. 107 013511
7Fujiwara KObinata YUjihara TUsami NSazaki GNakajima K 2004 J. Cryst. Growth 266 441
8Fujiwara KFukuda HUsami NNakajima KUda S 2010 Phys. Rev. 81 224106
9Yang X BFujuwara KGotoh RMaeda KNozawa JKoizumi HUda S 2010 Appl. Phys. Lett. 97 172104
10Fujiwara K2012Int. J. Photoenergy30311
11Hoyt J JAsta M2002Phys. Rev. B65392
12Ashkenazy YAverback R S 2010 Acta Mater. 58 524
13Sun D YHoyt J J2004Phys. Rev. B691129
14Majeed ALaird B B 2006 Phys. Rev. Lett. 97 216102
15Monk JYang YMendelev M IAsta MHoyt J JSun D Y2010Modell. Simul. Mater. Sci. Eng.18317
16Apte P AZeng X C 2008 Appl. Phys. Lett. 92 221903
17Hoyt J JAsta MKarma A 2003 Mater. Sci. Eng. 41 121
18Davidchack R LLarid B B 2005 J. Phys. Chem. 109 17802
19Zhang Y PLin XWei LPeng D JWang MHuang W D 2013 Acta Phys. Sin. 62 178105 (in Chinese)
20Li M EXiao Z YYang G CZhou Y H 2006 Chin. Phys. 15 219
21Hoyt J JSadigh BAsta MFoils S M 1999 Acta Mater. 47 3181
22Broughton JGilmer GJackson K 1982 Phys. Rev. Lett. 49 1496
23Tersoff J 1989 Phys. Rev. 39 5566
24Zhou N GHu Q FXu W XLi KZhou L2013Acta Phys. Sin.62146401(in Chinese)
25Tersoff J 1986 Phys. Rev. Lett. 56 632
26Tersoff J 1988 Phys. Rev. 38 9902
27Velet L 1967 Phys. Rev. 159 98
28Lutsko J FWolf DPhillpot S RYip S 1989 Phys. Rev. 40 2841
29Wang H LWang X XWang YLiang H Y 2006 Acta Phys. Chim. Sin. 22 1367 (in Chinese)
30Husiman W J.Peter J FDerks J WFicke H G 1997 Rev. Sci. Instrum. 68 4169
31Celestini FDebierre J M2002Phys. Rev. E65110
32Hashibon AAdler JFinnis M WKaplan W D2001Comp. Mater. Sci.24443
33Kob W1998J. Phys.: Condens. Matter11R85