The surface acoustic wave (SAW) is frequently used as an experimental tool to transport electrons in one-dimensional (1D) quantum lines as well as in two-dimensional electron gases (2DEGs).^[1,2] The SAW experiments in the 1D channel on GaAs-Al_xGa_1–xAs heterojunctions reveal quantized plateaus of acoustic-electric current which are proportional to the frequency of the acoustic wave, I = n · ef (n is an integer).^[3] It means that an integer number of electrons are pumped through the channel in one oscillating cycle of the SAW. A lot of theoretical works have attempted to interpret this quantum phenomenon.^[4–7] It is intuitively considered that the Coulomb-blockade effect may play a key role. The explicit mechanism, however, remains controversial. In Ref. [8], the authors discussed the precision of the plateaus and impurity of the potentials. Other works of modeling the quantized pump are based on the tight-binding model which consists of discrete quantum dots and two leads connecting the electron reservoirs on each side. The non-interacting electron transportation is expressed by reduced nearest-neighbor hopping amplitudes.^[9,10] This model is analogous to the discrete 1D Harper model which exhibits a non-trivial topological phase.^[11]

Topology as a mathematical conception has been serving the condensed matter physics for 30 years since the explanation of the quantized Hall effects. It has become a useful means in understanding the topological insulator,^[12] superconductivity,^[13–15] and the quantized charge or spin pump.^[16,17] It has been implemented in optical lattices^[18,19] and in graphene-like materials as well.^[20,21] In this paper, we propose a setup with a sequence of split metal gates in the 1D channel, creating a sequence of barrier potentials. We then explore the topology implications of the quantized charge pumping by a SAW within the band theory. In the quantized charge pumping process, the electrons follow an adiabatically varying potential.^[22] The surface acoustic wave is taken as a spatially periodical potential whose energy spectrum possesses the Bloch band structure, whereas the time-dependent phase plays the role of an adiabatic parameter of the Hamiltonian which induces a geometrical phase. The staircase-like acoustic currents are characterized by topological Chern numbers. We investigate the dependence of the number of pumped electrons on physical parameters such as the height of the barrier, the amplitude of the SAW and the Fermi levels and reveal a series of topological transitions. Based on this interpretation, we further predict a novel effect of quantized but non-monotonous current plateaus simultaneously pumped by two homodromous SAWs.

The 1D narrow channel was experimentally realized by a split metal gate on the surface of a GaAs-Al_xGa_1–xAs heterojunction. The time-dependent SAW potential induced by the piezoelectric effects is written as

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. Energy band structure of E versus time t for (a) V0 = 20ER and (b) V0 = 30ER. The amplitude of the SAW is fixed as VSAW = 30ER and q = 2. Panel (b) shows that a band crossing occurs between the 2nd and 3rd bands as V0 increases. Panels (c) and (d) are the topographical maps of the Berry curvature distributions for the 3rd and 4th bands at V0 = 20ER. The integrations over the BZ give rise to the Chern number of 0 and 1, respectively.

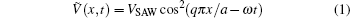
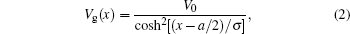
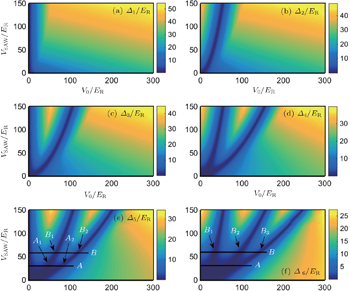
For the slowly oscillating SAW, the system can be treated as a quasi-static problem. The time-dependent phase δ = ωt is taken as a variable parameter that yields a Berry phase as δ changes to complete a cycle from 0 to π. The Bloch wave vector k is approximately a good quantum number at a given δ. The periodicity both in the k-space and the δ-space defines a 2D Brillouin zone (BZ). In the upper row of Fig. 1 we display the energy band structures versus the time or δ for two values of barrier height (a) V₀ = 20E_R and (b) V₀ = 30E_R at a fixed SAW amplitude V_SAW = 30E_R. Here E_R = ℏ²π²/2ma² is taken as the unit of energy. The dependence of E on the Bloch momentum k leads to broadening of the energy bands and the gaps vary with time. By comparing band structures shown in Figs. 1(a) and 1(b) which are plotted in the periodic scheme, we note that as V₀ increases, the energy gaps may close and reopen and level crossings take place between the adjacent bands.

The Berry curvature of a given band in the torus-shape BZ is defined as

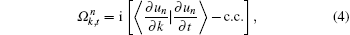
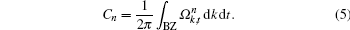
The Chern number of each band can be computed as long as they are well-separated. For example, the integrations of Berry curvature distributions in Figs. 1(c) and 1(d) give a Chern number of 0 and 1, respectively.

Table 1.

Table 1.

Table 1. Chern numbers Cn of the six lowest energy bands for various values of V0. The amplitude of the SAW is fixed at VSAW = 30ER. The slashes indicate that the Chern numbers are not well-defined due to closing of the gap. . V0(ER) 10 20 30 40 50 60 70 C1 0 0 0 0 0 0 0 C2 1 1 0 0 0 0 0 C3 0 0 1 1 0 0 0 C4 1 1 0 0 1 1 0 C5 / 0 1 1 0 0 1 C6 / / 0 0 1 1 0

Table 1. Chern numbers Cn of the six lowest energy bands for various values of V0. The amplitude of the SAW is fixed at VSAW = 30ER. The slashes indicate that the Chern numbers are not well-defined due to closing of the gap. .

Table 1 lists the Chern numbers of the six lowest bands versus V₀ for the model Hamiltonian (3) with q = 2. The amplitude of the SAW is fixed at V_SAW = 30E_R. The Chern numbers for V₀ = 0 are not shown, where the eigen equation is simply the Harper equation and the model is a sliding lattice. Each pair of adjacent bands corresponds to a single band of the V₀ = 0 model, e.g., C₁ + C₂ instead of C₁ or C₂ separately is well-defined. The change of V₀ opens or closes a gap, leading to jumps of the Chern number or topological transitions of the bands.

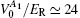
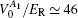
We examine the relation of the band topology with the system parameters. Figure 2 plots the six lowest gaps versus V₀ at different times ωt = 0, π/8, π/4, 3π/8, and π/2, respectively. The amplitude of the SAW potential is V_SAW =30E_R. From Fig. 2(b) we observe that the second energy gap is closed and reopened at V₀/E_R ≃ 24, which corresponds to the jump of the Chern number in C₂ and C₃ as displayed in Table 1. It implies that a topological transition occurs. The same transitions occur in the third gap at V₀/E_R ≃ 43 (Fig. 2(c)), in the fourth gap at and (Fig. 2(d)), and in the fifth gap at and (Fig. 2(e)), respectively. The topological transition points are intimately related to the closing points of the energy gaps.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. Energy gaps Δn versus the amplitudes V0 of the barrier potential at different time points ωt = 0 (blue), π/8 (red), π/4 (yellow), 3π/8 (purple), π/2 (green). Panels (a)–(f) correspond to n=1–6 gaps with VSAW = 30ER. The zeros of the curves indicate that the gaps vanish. As a comparison, panels (g) and (h) respectively illustrate Δ5 and Δ6 for a larger SAW amplitude VSAW = 60ER where the 6th gap is reopened because of nonzero Δ6. It means that the amplitude of the SAW modifies the topology of the energy bands.

On the other hand, topological transitions can also be implemented by adjusting the SAW amplitude V_SAW. As V_SAW increase from 30E_R (Fig. 2(f)) to 60E_R (Fig. 2(h)), gap-closing points appear at B₁, B₂, and B₃. To give a complete description of the relations of the band topology with the system parameters, we show in Fig. 3 the topographical map of the minimum gaps in the time period versus V₀ and V_SAW. The horizontal lines A and B in Figs. 3(e) and 3(f) mark V_SAW = 30E_R and V_SAW = 60E_R, respectively. The crossing points A₁, A₂, and B₁ and B₂ in Fig. 3(e) correspond to the transition points in Figs. 2(e) and 2(g). Accordingly, the points B₁, B₂, and B₃ in Fig. 3(f) correspond to the transition points in Fig. 2(h).

For the particle pumping, we adopt the adiabatic approximation analysis of the geometric phase^[25–27] by considering that the velocity of the acoustic wave is much smaller than the Fermi velocity,^[28,29]

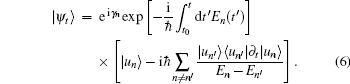
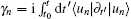
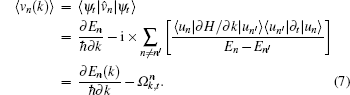
It satisfies the time-dependent Schrödinger equation iℏ∂_t|ψ_t⟩ = Ĥ(t)| ψ_t⟩. We have used the instantaneous eigenstates (the Bloch states) |u_n⟩ of the Hamiltonian Ĥ(t) and . The system has a complete temporal dependence on the SAW potential, which is periodically varying with the period T = π/ω. The expectation of the velocity operator v̂_n = ∂H(k,t)/∂(ℏk) is

The last equivalence is obtained by making use of the relation ⟨u_n|∂H/∂k|u_n′⟩ = (E_n − E_n′)⟨∂u_n/∂k|u_n′⟩. Here insulating states rather than conducting states contribute to the induced current, thus only initially full-filled bands are of concern. The pumping current is the integration of ⟨v_n(k)⟩ over the BZ, in which the zeroth-order term vanishes. The total number of particles pumped in an oscillating cycle is

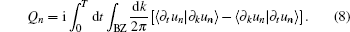
This is exactly the Chern number calculated from formulism (5). It demonstrates that the adiabatic pumping is quantized and the total number of pumped particles is equal to the summation of the Chern numbers of all completely filled bands. Thus the Fermi level should also be considered to determine the amount of bands that are of concern.

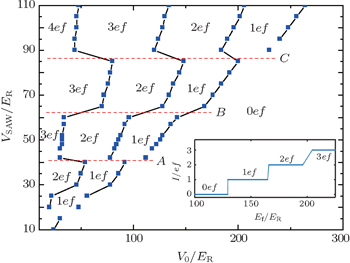
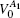
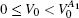
For example, if the lowest four bands are occupied, there are two transition points A₁ and A₂ in Fig. 2(d) as V₀ increases. We notice that is also the transition point of the second gap, as shown in Fig. 2(b). Consequently, there exist two quantized current plateaus. In the same way, the two transition points A₁ and A₂ in Fig. 2(e) indicate three current plateaus of I = 2ef for , , and I = 0 for . Here f = ω/π is the frequency of the SAW. In order to obtain higher current plateaus, one just needs to implement a larger SAW amplitude in which more electrons are classically trapped in a spatial period. In our frame of analysis, we need more transition points in the well-separated gaps, as the transition points B₁, B₂, and B₃ in the fifth (Fig. 2(g)) and sixth gaps (Fig. 2(h)) for a larger SAW amplitude V_SAW = 60E_R.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Topographical map of the minimum energy gaps Δn (n = 1–6) versus V0 and VSAW. The map is divided into several regimes by valleys where band gaps are closed. The rightmost region corresponds to the lowest plateaus of a pumping current of I = 0ef. The plateaus rise up from 0ef to ne f (with an integer n) while we assign parameters from lower right areas to upper left ones.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Phase diagram of current plateaus versus V0 and VSAW. Each region corresponds to the summation of Chern numbers of the filled bands. Inset: schematic plot of staircase-like pumping current versus the Fermi energy for VSAW = V0 = 100ER.

Based on the above analysis, in Fig. 4 we summarize the current plateau diagram versus V₀ and V_SAW. Each region is labeled by the summation of Chern numbers of the well-separated bands. The ‘phase’ boundary is determined by the closing point of the gaps. Deeper insights into the transitional issues at these boundaries are beyond the capability of topological interpretation. Experimentally, the boundary may be broadened due to thermal fluctuations. The gap must be large enough so that the insulating condition is satisfied. We argue that a partially-filled band has no contributions to the current induced by adiabatic pumping. Our theoretical treatment of non-interacting electrons qualitatively agrees with the experimental observations.^[8,30]

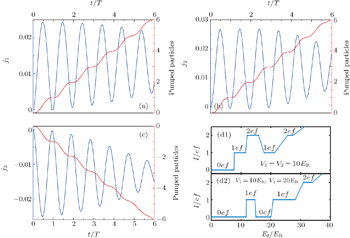
The performance of SAW in split gates without gate voltage is simply a sliding potential, which gives rise to the standard of particle pumping. An extended research has confirmed the equivalence between topological properties and quantized charge pumping of a continuous Rice–Mele pump.^[19] In this section, we study the pumping effect of two sinusoidal SAWs with different spatial period but the same temporal frequency. The two SAWs have the same acoustic velocity. It can be realized by implementing an additional SAW propagating at an angle θ to the direction of the 1D channel. Explicitly, we consider the following SAW potential,

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. Pumping currents (blue line) and particle number (red line) by the SAW potential (9) in panel (a) the first band, (b) the second band, and (c) the third band, respectively. Note that the pumping current is reversed in the third band, which is related to the Chern number C3 = −1. (d) Non-monotonous current plateaus versus the Fermi energy for V1 = 10ER. Upper panel (d1): V3 = 10ER. Lower panel (d2): V3 = 20ER.

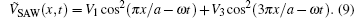
The Chern number of each band can be computed in the same way. For V₁ = V₃ = 10E_R, the Chern numbers of the lowest four bands are C_n = 1, 1, − 1, 1. It is straightforward to calculate the current and pumped number of particles. Figure 5 shows the pumping currents of the three lowest bands. Each band contributes exactly one particle in an oscillating circle. Figure 5(c) indicates a pump in the negative direction, which corresponds to the Chern number C₃ = −1. The current plateaus are depicted according to the band structure and the Chern invariants, as shown in Fig. 5(d1). The pumping currents exhibit a non-monotonous rather than the staircase-like behavior. For V₁ = 10E_R and V₃ = 20E_R the Chern numbers of the lowest four bands are C_n = 1, −1, 1, 1. The pumping current is zero if the lowest two band are filled, as shown in Fig. 5(d2).

Finally, if we keep V₁ = 30E_R while increasing the second SAW amplitude from V₃ = 30E_R to V₃ = 40E_R, we can observe a jump from the I = 3ef plateau to the I = 1ef plateau. In this case, the Chern numbers of the four lowest bands experience a transition from C_n = 1, 1, 1, −1 to C_n = 1, 1, −1, 1.

In summary, we have investigated the SAW pumping effects in a 1D channel with barrier potentials caused by the gate voltage. The quantized pumping of electrons is interpreted in the viewpoint of topological invariants of the filled bands. The jump between two adjacent current plateaus is related to a topological transition. One of the benefits of topological theory is that the quantized plateaus are robust against perturbations as long as the gap keeps finite. Based on our interpretation, we predicted non-monotonous current plateaus pumped by two homodromous SAWs. Our prediction can be readily verified by current experiment techniques.^[31,32]