† Corresponding author. E-mail:
Project supported by the National High Technology Research and Development Program of China (Grant No. 2014AA041402) and the National Natural Science Foundation of China (Grant Nos. 51272276 and 51322211).
We report the observation of spectral broadening induced by 200 femtosecond laser pulses with the repetition rate of 1 kHz at the wavelength of 532 nm in semi-insulating 4H–SiC single crystals. It is demonstrated that the full width at half maximum of output spectrum increases linearly with the light propagation length and the peak power density, reaching a maximum 870 cm−1 on a crystal of 19 mm long under an incident laser with a peak power density of 60.1 GW/cm2. Such spectral broadening can be well explained by the self-phase modulation model which correlates time-dependent phase change of pulses to intensity-dependent refractive index. The nonlinear refractive index n2 is estimated to be 1.88×10−15 cm2/W. The intensity-dependent refractive index is probably due to both the nonlinear optical polarizability of the bound electrons and the increase of free electrons induced by the two-photon absorption process. Super continuum spectra could arise as crystals are long enough to induce the self-focusing effect. The results show that SiC crystals may find applications in spectral broadening of high power lasers.
The development of femtosecond (fs) laser pulses has emerged as a new means to study the ultrafast dynamic processes and the responses of matters under strong fields. For example, the non-thermal melting in semiconductors has been observed recently on the fs timescale using the ultrafast time-resolved x-ray diffraction which provides a direct probe of the changing of the atomic structure.[1,2] The distortion of the electrons or/and atoms will temporarily modulate the refractive index which will in turn modify the beam of light as it passes through the medium.[3] Spectral broadening, a phenomenon that occurs when an ultrafast pulse travels through the matters, has been observed in different transparent media, such as crystals,[4–6] liquids[7] or even gases.[8] The frequency broadening or continuum spectral pulses with fs duration as a tunable probe light source are useful in characterizing pump-probe spectroscopy of ultrafast process.[9–13] So far, it is usually generated by using crystals such as fused silica,[4] BaF2,[5] and CaF2.[6] But these crystals often suffer from damage associated with the self-focusing effect due to their low damage thresholds. It is desirable to explore new crystals with high damage thresholds for producing continuum spectra with high energy density.
Silicon carbide (SiC), an important wide bandgap semiconductor, has found wide applications in electronic and optoelectronic devices working under harsh conditions[14–16] for its superior properties,[17] such as high thermal conductivity, high band energy, excellent environmental resistance, and so on. SiC has more than 200 polytypes for the different stacking sequence of silicon-carbon double atomic layers along the crystallographic c axis. Among them, 6H– and 4H–SiC are the most common ones and commercially available. Our previous work[18] has successfully demonstrated the generation of mid-infrared (MIR) radiation by phase-matched difference frequency generation using semi-insulating (SI) 4H–SiC as the nonlinear optical crystal. MIR pluses on the fs scale were gathered through optical parametric amplifier process later on, which attests that 4H–SiC is appropriate for ultra-fast optical devices for its low group velocity mismatch.[19] The results open a door to practically utilize SI 4H–SiC crystals in high density and ultra-short laser fields. For this purpose understanding the spectral distribution of an ultra-fast laser beam propagating through 4H–SiC crystals is of importance. Meanwhile, 4H–SiC is expected to be a good candidate for generating high energy density continuum ultra-fast laser to meet practical demands considering its good transmittance,[18] high thermal conductivity,[17] and a high damage threshold of 80 GW/cm2,[20] which is several magnitudes higher than the above mentioned traditional crystals used for continuum spectra generating.
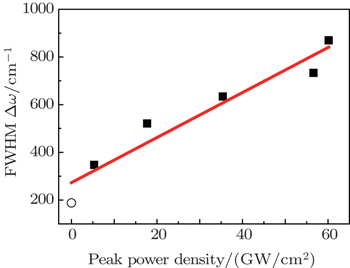
Here we present our results on the investigation of induced symmetric Stokes and anti-Stokes spectral broadening using SI 4H–SiC crystals as transparent media pumped by an incident laser with peak power densities varying from 5.3 GW/cm2 to 60.1 GW/cm2 at 532 nm and 200-fs duration at 1-kHz repetition rate. The full width at half maximum (FWHM) of the broadening spectrum reaches the maximum of about 870 cm−1 on a 19-mm long 4H–SiC pumped by a laser with the peak power density of 60.1 GW/cm2. It is demonstrated that the FWHM of the broadening spectrum increases linearly with the light propagation length in crystal and the peak power density, which can be well explained by the self-phase modulation (SPM) model. The results reveal a new effect of fs laser pulses on SiC crystals and may be useful in developing SiC-based high power optical devices in the future.
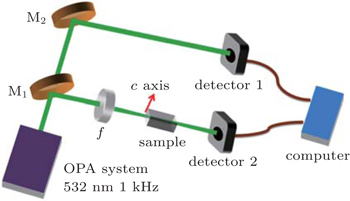
Quality SI 4H–SiC single crystal (TankeBlue, Beijing) was grown by physical vapor transport method with an FWHM of x-ray diffraction rocking curve 25.2 arcsec. Three samples with the lengths of 4.5 mm, 14 mm, and 19 mm perpendicular to the crystallographic c axis (optic axis) were cut from a 2 inch (1 inch = 2.54 cm) SI 4H–SiC ingot. The light entering surface (6 mm × 6 mm) of the sample was parallel to the optic axis and polished with a surface roughness below 0.3 nm.
The experimental setup for spectral broadening is schematically illustrated in Fig.
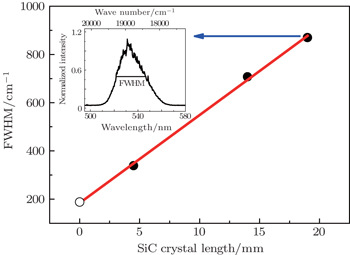
Figure
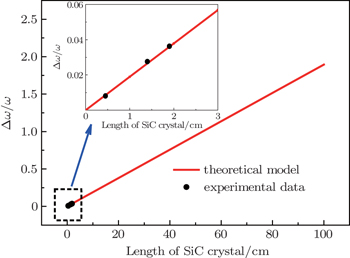
Since the spectral broadening is proportional to the light path in crystal, we focus on the SI 4H–SiC crystal with length of 19 mm to investigate the dependence of spectral broadening on the peak power density of incident beam. As shown in Fig.
The intensity-dependent spectral broadening indicates that the refractive index of SiC is influenced by the strong photoelectric field of fs laser pulses. Conclusively, the refractive index increases with increasing light intensity and can be written as n = n0 + n2I, where n0 represents the linear refractive index at the incident wavelength, I denotes the time-averaged intensity of the optical field and n2 is the nonlinear refractive index of the crystal. This intensity-dependent refractive index will produce a shift in the instantaneous phase of the pulses. For a laser pulse with on-axis intensity distribution I(z,t) propagating a distance L in a medium, the accumulating on-axis nonlinear phase distribution Δϕ is given by,
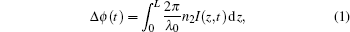
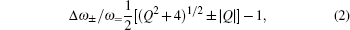
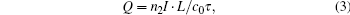
The spectral broadening Δω/ω increases linearly with the interaction length of 4H–SiC crystal, which means that the spectrum could be efficiently broadened with longer crystals or fibers with appropriate lengths as nonlinear optical media.
Considering the refractive index of 4H–SiC is light intensity dependent, the refractive index will not be uniform across the beam area. The maximum will be achieved at the center of the beam with a radial Guassian intensity distribution, possibly leading to the focusing of the laser beam toward the center portion,[23,24] which is called self-focusing effect. Tightening of the laser beam will cause concentration of energy which in turn assists the intensity-dependent SPM process. When the pump power exceeds the self-focusing critical power, the beam will collapse into a focus after propagating a certain distance of Zsf. The self-focusing length is given according to:[25]
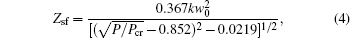
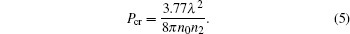
The physical origin of the spectral broadening here can be ascribed to the intensity-dependent refractive index change in the medium. In principle, the intense optical field can induce an appreciable refractive index change which is proportional to the third-order nonlinear susceptibility χ(3) in a medium. The positive change of nonlinear refractive index can arise from several mechanisms, acting on a broad range of timescales. In the case of a laser pulse with fs time input, the intense optical field distorts the electron distribution in real space, leading to the electron cloud polarization in the SiC crystal. The third-order nonlinearity polarization gives rise to the positive change of the refractive index. On the other hand, the positive change in refractive index of SiC can also be caused by the sufficiently high density of free electrons in the conduction band.[23] In a strong photoelectric field, one can expect that multiphoton resonant excitations will occur. Theoretical analysis shows that the two-photon absorption coefficient reaches its maximum when ħω/Eg is about 0.7, where ħω is the photon energy and Eg is the bandgap of the semiconductor.[27,28] This value is evaluated to be 0.73 for SI 4H–SiC crystal with bandgap of 3.2 eV under the incident laser at 532 nm. Additionally, previous works showed that electrons in SiC crystals exhibit ultrafast optical response on the fs scale.[22,29] In the current case, two-photon absorption would most likely occur, leading to the laser-induced promotion of a large fraction of the valence electrons to the conduction band, in which the inter-atoms forces will be modified and the lattice atoms immediately begin to move away from the equilibrium position on fs timescale.[1] In other words, the fs pulses displace electrons or/and cause lattice changes which will result in a modification to the refractive index.[3] In a word, the nonlinear refractive index is related both to the optical polarizability of the bound electrons in real space and the increase of the free electrons in the conduction band of SiC crystals.
We report that SI 4H–SiC can be a new material for spectral broadening when pumped by fs laser pulses with the wavelength of 532 nm. The FWHM of the spectral broadening increases linearly with the propagation length and the peak power density of the incident laser. The mechanism is mainly attributed to the self-phase modulation caused by the intensity-dependent nonlinear refractive index which is related to the third-order nonlinear susceptibility. The spectral broadening is not so large mainly due to the insufficiency of the crystal length along the light propagation direction. The super-continuous spectra could be expected using higher intensity pulses and SiC crystals or fibers with appropriate lengths.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 |