† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61503280, 61403278, and 61272006).
This paper investigates the H∞ synchronization of the coronary artery system with input delay and disturbance. We focus on reducing the conservatism of existing synchronization strategies. Base on the triple integral forms of the Lyapunov–Krasovskii functional (LKF), we utilize single and double integral forms of Wirtinger-based inequality to guarantee that the synchronization feedback controller has good performance against time-varying delay and external disturbance. The effectiveness of our strategy can be exhibited by simulations under the different time-varying delays and different disturbances.
In recent decades, chaos has combined with biological engineering due to it being widely encountered in the nervous system, brain activity, epidemic diseases and coronary artery system.[1–3] The coronary artery system is a complex system which conveys oxygen and nutrients to the myocardium day and night. Healthy coronary artery vessels are important to maintain our life. In clinical practice, myocardial infarction caused by obstructing or spasm of the coronary artery will threaten our life. Due to its important effect on our health, this system deserves considerable attention in many areas. With the development of nonlinear science, researchers made a lot of effort in the investigation of the coronary artery system. Based on the muscle mechanics model, Guanggui Bao proposed the mechanics equation of the coronary artery vessel. Utilizing this equation, the mathematical model of the coronary artery vessel is derived in Ref. [4]. We find that this model is a chaotic system.
Since the coronary artery system can be described as a chaos system, many studies of the coronary artery system are focusing on synchronization of a chaotic system. From a medical point of view, when myocardial infarction occurs, the coronary artery vessel must be thrown into convulsion. It will cause degraded performance of oxygen supply to the myocardium. In order to alleviate this symptom, some emergency medicine should be adopted to expand the coronary artery vessel, such as glyceryl trinitrate. From the perspective of mathematics, glyceryl trinitrate can make the diseased coronary artery vessel synchronize with the healthy one by changing the inner diameter and pressure of the vessel. Therefore, chaotic synchronization of the coronary artery system is an essential work. Reference [5] utilized a backstepping method to achieve chaos synchronization. Reference [6] used a nonlinear state feedback approach to design a controller for the coronary artery system. Considering the structure uncertainties, reference [7] proposed a sliding mode control based chaos synchronization strategy for the coronary artery system. By applying high-order sliding mode adaptive control approach, Zhao et al. studied the finite-time chaos synchronization problem; this approach can obtain a good effect even though the information of perturbation bound is unknown.[8]
However, there are some things worth noting. First, between the paroxysm of myocardial infarction and taking medicine there is always some time lag. Not only that, the effect of medication on the coronary artery will have some delay because the absorbing of medication will cost some time. It is not difficult to understand that the time delays mentioned above are not fixed. That is to say, considering the actual situation the input time-varying delay should not be ignored. Unfortunately, aforementioned literature did not consider that. It is not hard to imagine that if we fail to input time-varying delay, the performance of the existing control strategy will decline even failure.
Time delay is widely encountered in communication systems, neural networks, economic systems, biological systems, and networked control systems.[9–12] Since time delay will cause serious degradation of system performance, in the last few decades a lot of researchers have been making considerable effort to reduce the influence that comes from time delay. Jensen’s inequality plays an important role in a lot of existing literature. However, it will induce some conservativeness hard to overcome. In order to reduce the conservatism, Wirtinger-based integral inequality,[13] which can be used to obtain even tighter lower bound of single integral terms was proposed. Very recently, a Wirtinger-based double integral inequality was proposed to get even tighter lower bound of double integral terms.[14]
As well as the input of time-varying delay, as a practical system, the coronary artery system must have many nonlinear disturbances which come from the external environment or emotion. These disturbances will make the performance of control strategy decrease seriously. To counter these nonlinear disturbances, lots of techniques have been proposed, such as adaptive tracking control,[15] model predictive control,[16,17] fuzzy control,[18–21] sliding mode control.[22–26] H∞ control is a valid approach to reduce the effect caused by disturbances. As the application of H∞ control, H∞ synchronization for a chaotic system is studied in Ref. [27]. A criterion for existence of the controller can be given in terms of LMIs. Using the LMI box, the feasible solutions of LMIs can be obtained.
Motivated by the previous discussions, we research H∞ synchronization of the coronary artery system with input time-varying delay and external disturbances. Based on LKF approach and LMI method, we propose a new control strategy. In this strategy, the triple integral forms of LKF, Wirtinger-based inequality and double integral forms of Wirtinger-based inequality will be used to reduce the conservative. It means that the new strategy can ensure the effectiveness of the controller under the appropriate input time-varying delay. Moreover, H∞ control approach has been introduced to conflict with the disturbances. Some simulations show that this control strategy still has better robustness under the input time-varying delay.
The coronary artery vessels supply oxygen and nutrients for the myocardium. The mathematical model of the coronary artery vessel is derived in Ref. [4], which can be written as a Duffing equation:
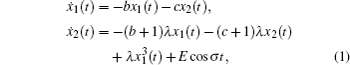
In order to facilitate expression, system (1) can be written as follows:

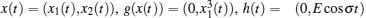

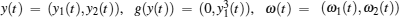

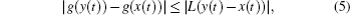
When ω(t) = 0 and the initial conditions of systems (
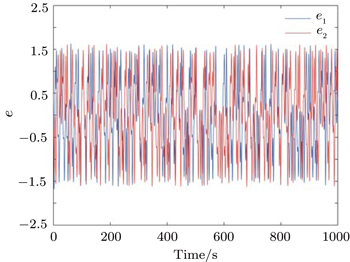
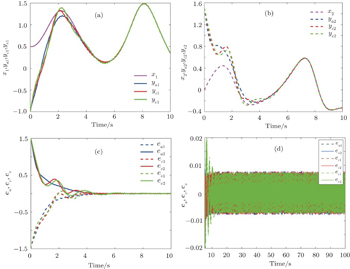
From Fig.
In order to derive the new control strategy, the following lemmas will be used.
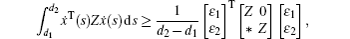

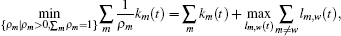
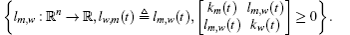
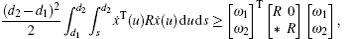

In this section, we get a new synchronization method by using the aforementioned Lemmas.
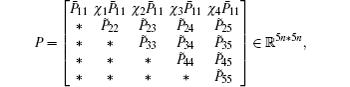
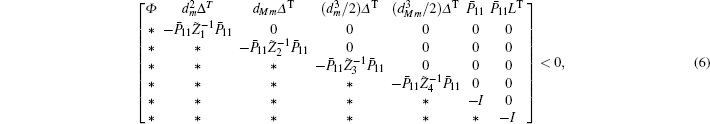

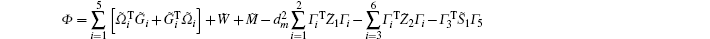
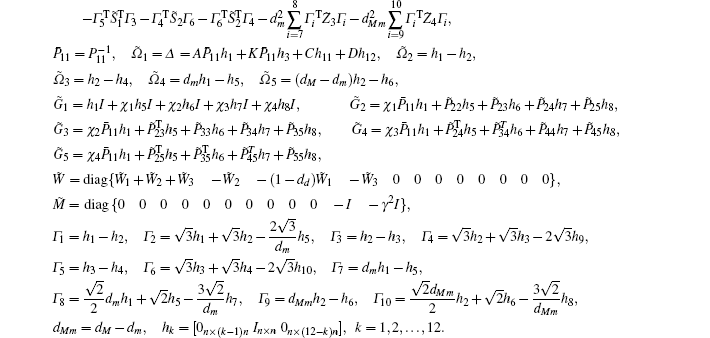
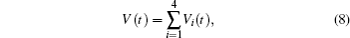



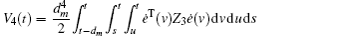
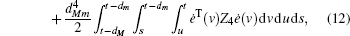
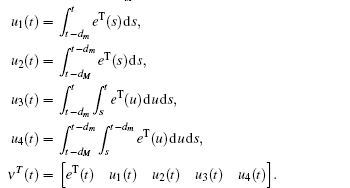
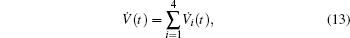



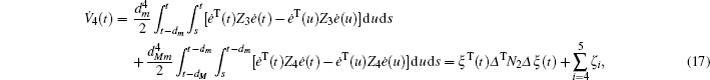
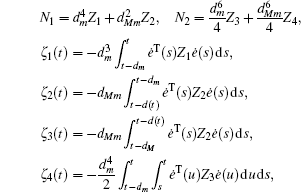
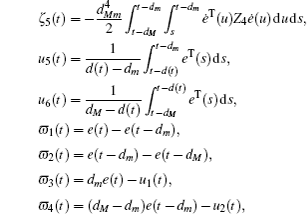
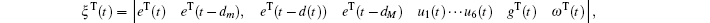
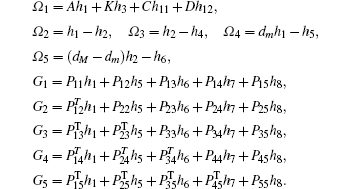

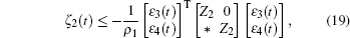
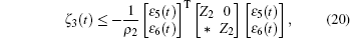
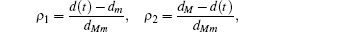

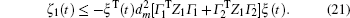
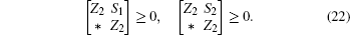
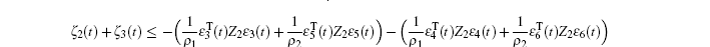
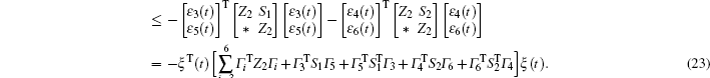
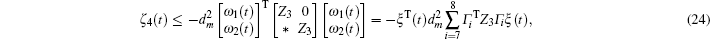


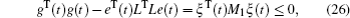
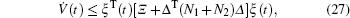
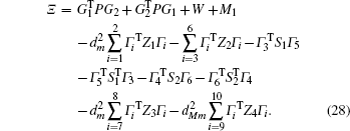

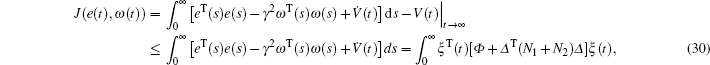

Multiplying both sides of Φ with
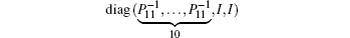
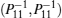
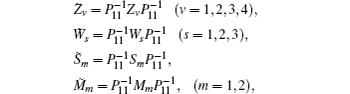

We still cannot obtain a feasible solution by LMI tool box according to Theorem 1 because there are nonlinear terms in the form of 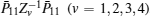
First, define new variables Uv (v = 1,2,3,4), satisfying
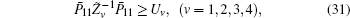

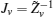
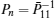
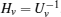
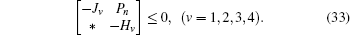
Minimize
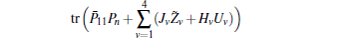
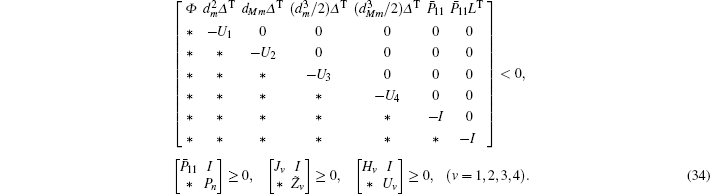
For given scalars dm, dM, dd, χκ − 1 (κ = 1,2,3,4), find a feasible set Solve minimization problem with

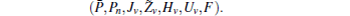

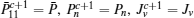
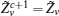
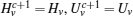
If linear matrix inequalities (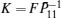
In this section, numerical examples are given to demonstrate the effectiveness of the proposed strategy.
Considering coronary artery systems (
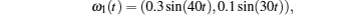
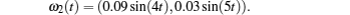
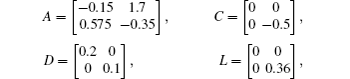
The above three cases illustrate the performance of Theorem 1. Figures
In this paper, considering the disturbance comes from the external environment or emotion and the time delay caused by taking medicine and drug absorption, we research the chaotic synchronization for the coronary artery system. We utilize LKF approach, LMI method, and some advanced inequality technology to reduce the conservatism. From the simulations, we can see our synchronization strategy is valid to make the convulsing coronary artery system synchronize with the healthy coronary artery system under the input delay and external disturbance. As a part of our body, the coronary artery system is an extremely complicated system. Therefore, it is difficult to obtain a precise model of this system. With the development of active shape models[30] and the computer control technology,[31] we can derive accurate models of the coronary artery system in our future work.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 |