Cite this Article
Zhang Yan, Duan Li, Ji Vincent, Xu Ke-Wei. First-principles study of the structural, electronic, and magnetic properties of double perovskite Sr2FeReO6 containing various imperfections. Chinese Physics B, 2016, 25(5): 058102  
Permissions
First-principles study of the structural, electronic, and magnetic properties of double perovskite Sr2FeReO6 containing various imperfections
Zhang Yan1, †, , Duan Li1, Ji Vincent2, Xu Ke-Wei3
School of Materials Science and Engineering, Chang'an University, Xi'an 710061, China
ICMMO/SP2M, UMR CNRS 8182, Université Paris-Sud, 91405 Orsay Cédex, France
State Key Laboratory for Mechanical Behavior of Materials, Xi'an Jiaotong University, Xi'an 710049, China

 

† Corresponding author. E-mail: yan.zhang@chd.edu.cn

Project supported by the National Natural Science Foundation of China (Grant No. 51501017).

Abstract
Abstract

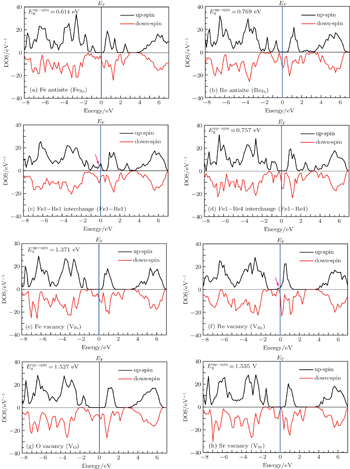
The structural, electronic, and magnetic properties of double perovskite Sr2FeReO6 containing eight different imperfections of FeRe or ReFe antisites, Fe1–Re1 or Fe1–Re4 interchanges, VFe, VRe, VO or VSr vacancies have been studied by using the first-principles projector augmented wave (PAW) within generalized gradient approximation as well as taking into account the on-site Coulomb repulsive interaction (GGA+U). No obvious structural changes are observed for the imperfect Sr2FeReO6 containing FeRe or ReFe antisites, Fe1–Re1 or Fe1–Re4 interchanges, or VSr vacancy defects. However, the six (eight) nearest oxygen neighbors of the vacancy move away from (close to) VFe or VRe (VO) vacancies. The half-metallic (HM) character is maintained for the imperfect Sr2FeReO6 containing FeRe or ReFe antisites, Fe1–Re4 interchange, VFe, VO or VSr vacancies, while it vanishes when the Fe1–Re1 interchange or VRe vacancy is presented. So the Fe1–Re1 interchange and the VRe vacancy defects should be avoided to preserve the HM character of Sr2FeReO6 and thus usage in spintronic devices. In the FeRe or ReFe antisites, Fe1–Re1 or Fe1–Re4 interchanges cases, the spin moments of the Fe (Re) cations situated on Re (Fe) antisites are in an antiferromagnetic coupling with those of the Fe (Re) cations on the regular sites. In the VFe, VRe, VO, or VSr vacancies cases, a ferromagnetic coupling is obtained within each cation sublattice, while the two cation sublattices are coupled antiferromagnetically. The total magnetic moments μtot (μB/f.u.) of the imperfect Sr2FeReO6 containing eight different defects decrease in the sequence of VSr vacancy (3.50), VRe vacancy (3.43), FeRe antisite (2.74), VO vacancy (2.64), VFe vacancy (2.51), ReFe antisite (2.29), Fe1–Re4 interchange (1.96), Fe1–Re1 interchange (1.87), and the mechanisms of the saturation magnetization reduction have been analyzed.

PACS: 81.05.Je;71.55.Jv;71.23.–k;75.25.–j;
Keyword:double perovskite;imperfections;electronic properties;magnetic properties;
1. Introduction

Over the past few decades, magnetic double perovskites with a general chemical formula of A2 BB′O6, where A is an alkaline earth metal or rare earth metal cation, and B and B′ are 3d and 4d/5d transition-metal (TM) cations, respectively, have been studied, especially the finding of the intrinsic tunneling magnetoresistance (TMR) effect at room temperature in Sr2FeMoO6[1] and Sr2FeReO6[2] revives the extensive study of the double perovskites A2 BB′O6. Bandstructure calculations reveal that they have a ferrimagnetic (FiM) half-metallic (HM) character with completely (100%) spin-polarized transport properties at the Fermi level.[1,2] The Curie temperatures TC of Sr2FeMoO6 and Sr2FeReO6 are found to be fairly high, as high as 415 K and 401 K, respectively, making them potential candidates for industrial applications in magnetoresistive[3] and spintronics[4] devices at room temperature. Besides experimental works,[1,2,5–13] various first-principles methods[1,2,14–19] including the local spin density approximation (LSDA) and the generalized gradient approximation (GGA) have been used to investigate the electronic and magnetic properties of the ordered Sr2FeMoO6 and Sr2FeReO6. It has been found that at the ground state, the Fe3+(3d5) is in the high spin state of S = 5/2 according to Hund’s rule, and Mo5+(4d1) and Re5+(5d2) are highly ionized with valence spin states of S = 1/2 and S = 1, respectively. Each of the two TM sites, namely, the Fe3+ (3d5, S = 5/2) and Mo5+ (4d1, S = 1/2) or Re5+ (5d2, S = 1) sites, is believed to be ferromagnetically (FM) arranged within each sublattice, while the two sublattices are coupled antiferromagnetically (AFM), giving rise to the total spin magnetic moments of 4 μB and 3 μB per formula unit (f.u.) for Sr2FeMoO6 and Sr2FeReO6, respectively. The smaller saturation magnetizations of 3 μB/f.u. and 2.7 μB/f.u. at 4.2 K for Sr2FeMoO6[1] and Sr2FeReO6[2] respectively are attributed to the mis-site-type disorder of the TM sites.[20–22]

Growth of the double perovskites Sr2FeMoO6 and Sr2FeReO6 would always lead to a certain degree of imperfections. For instance, Kobayashi et al.[1] found that 13% of the Fe and Mo cations in their sintered Sr2FeMoO6 are not on the respective sublattices. It is theoretically and experimentally shown that the ordering of the TM Fe and Mo/Re as well as the oxygen vacancy are the key factors determining the macroscopic magnetic properties of Sr2FeMoO6 and Sr2FeReO6. The antisite defects, which are defined as the misplacement of Fe in Mo/Re positions and vice versa, and the oxygen vacancy generally decrease the saturation magnetization and the Curie temperature TC.[1,9,10,20–32] Among those works, only Retuerto et al.[32] investigated the effects of the inherent imperfections on the properties of Sr2FeReO6 experimentally, they found that the sample prepared by a soft-chemistry technique presents 75% of Fe/Re cationic order and an enhanced Curie temperature of 445 K, while the one prepared by the high-pressure method generates a complete Fe/Re cationic order and a superior saturation magnetization. The other experimental and theoretical works on Sr2FeReO6 are about the external impurity substitution defects. Experimentally, Jung et al.[9] found that the FiM behavior of Sr2FeReO6 changes to the AFM upon Sb substitution. Jung et al.[10] studied the effects of diamagnetic dilution of the Fe sublattice on the structural and magnetic properties of Sr2Fe1−xGaxReO6. They found that the amount of antisite disorder increases with increasing Ga content. For 0 < x < 0.4, only a tetragonal and magnetically ordered phase is detected. A phase separation into a tetragonal phase and a cubic phase is detected for x ≥ 0.4. The soft-chemistry method was also used by Blanco et al.[33] to fabricate Sr2FeReO6, Sr2FeRe0.9Nb0.1O6, and Sr2FeRe0.9Ta0.1O6. The lower magnetic moments compared to the theoretical ones were attributed to the antisite disorder of 25% in the B and B′ positions. Blasco et al.[34] found that the replacement of Sr by La leads to an increase of the unit cell volume and a rise of the Curie temperature. However, both the saturated magnetic moment and the room-temperature magnetoresistance decrease with increasing La content. Theoretically, the effects of Cr substituting for Fe,[35] La substituting for Sr,[36] and Tc substituting for Re[37] on the structural, electronic, and magnetic properties of Sr2FeReO6 have been investigated by using the first-principles calculations within the density function theory (DFT) framework. Therefore, in this paper, on the point of view of the HM character and magnetization reduction, the structural, electronic, and magnetic properties of the imperfect double perovskite Sr2FeReO6 containing eight different inherent defects of Fe antisite (FeRe), Re antisite (ReFe), Fe1–Re1 interchange (Fe1–Re1), Fe1–Re4 interchange (Fe1–Re4), Fe vacancy (VFe), Re vacancy (VRe), O vacancy (VO), and Sr vacancy (VSr) are studied by using first-principles projector augmented wave (PAW) within generalized gradient approximation as well as taking into account the on-site Coulomb repulsive interaction (GGA+U).

2. Calculation method and models

The calculations are performed using the Vienna ab initio simulation package (VASP) based on the DFT.[38–41] The interaction between electron and ionic core is represented by the projector augmented wave (PAW) potentials,[42] which are more accurate than the ultra-soft pseudopotentials. To treat the electron exchange and correlation, we choose the Perdew–Burke–Ernzerhof (PBE)[43] formulation of the generalized gradient approximation (GGA). We take into account the on-site Coulomb repulsive interaction (GGA+U) with the effective U parameters of 2.0 eV for Fe and 1.0 eV for Re,[15,44] which yields the correct ground state structure of the strong correlation system. A conjugate-gradient algorithm is used to relax the ions into their ground states, and the energies and the forces on each ion are converged within 1.0 × 10−4 eV/atom and 0.02 eV/Å, respectively. The cutoff energy for the plane-waves is chosen to be 450 eV. The Sr 4s24p65s2, Fe 3d64s2, Re 5d56s2, and O 2s22p4 electrons are treated as valence electrons. The k-points are sampled according to the Monkhorst–Pack automatic generation scheme with their origin at the Γ point[45] and 10 divisions in each direction, together with a Gaussian smearing broadening of 0.1 eV.

In order to compare the electronic structures of the imperfect and the perfect Sr2FeReO6 on the same footing, the calculations are all performed by constructing a supercell of 4 f.u. (Sr8Fe4Re4O24). As compared with Fig. 1(i) for perfect Sr8Fe4Re4O24, eight different configurations of the defects (marked with circles) are considered: (a) Fe antisite (FeRe) at (0.5, 0.5, 0.5) site (Sr8Fe5Re3O24), (b) Re antisite (ReFe) at (0, 0.5, 0.5) site (Sr8Fe3Re5O24), (c) Fe1–Re1 interchange (Fe1–Re1) at (0, 0, 0) and (0, 0, 0.5) sites (Sr8Fe4Re4O24), (d) Fe1–Re4 interchange (Fe1–Re4) at (0, 0, 0) and (0.5, 0.5, 0.5) sites (Sr8Fe4Re4O24), (e) Fe vacancy (VFe) at (0, 0.5, 0.5) site (Sr8Fe3Re4O24), (f) Re vacancy (VRe) at (0.5, 0.5, 0.5) site (Sr8Fe4Re3O24), (g) O vacancy (VO) at (0.5, 0.5, 0.25) site (Sr8Fe4Re4O23), and (h) Sr vacancy (VSr) at (0.75, 0.75, 0.75) site (Sr7Fe4Re4O24).

Fig. 1. Optimized structures of imperfect (marked with circles) Sr2FeReO6 of 4 f.u. containing (a) Fe antisite (FeRe), one Fe atom substituting for one Re atom at (0.5, 0.5, 0.5) site (Sr8Fe5Re3O24), (b) Re antisite (ReFe), one Re atom substituting for one Fe atom at (0, 0.5, 0.5) site (Sr8Fe3Re5O24), (c) Fe1–Re1 interchange (Fe1–Re1), exchanging Fe and Re positions respectively at (0, 0, 0) and (0, 0, 0.5) sites (Sr8Fe4Re4O24), (d) Fe1–Re4 interchange (Fe1–Re4), exchanging Fe and Re positions respectively at (0, 0, 0) and (0.5, 0.5, 0.5) sites (Sr8Fe4Mo4O24), (e) Fe vacancy (VFe), removing one Fe atom from (0, 0.5, 0.5) site (Sr8Fe3Re4O24), (f) Re vacancy (VRe), removing one Re atom from (0.5, 0.5, 0.5) site (Sr8Fe4Re3O24), (g) O vacancy (VO), removing one O atom from (0.5, 0.5, 0.25) site (Sr8Fe4Re4O23), and (h) Sr vacancy (VSr), removing one Sr atom from (0.75, 0.75, 0.75) site (Sr7Fe4Re4O24). The optimized structure of the perfect Sr2FeReO6 of 4 f.u. (Sr8Fe4Re4O24) is also shown in panel (i) for comparison.
3. Results and discussion
3.1. Relaxed structures

The relaxed structures of 4 f.u. Sr2FeReO6 with eight different defects (marked with circles) are shown in Figs. 1(a)–1(h) together with the perfect one in Fig. 1(i) for comparison. From Figs. 1(a)–1(d), we can see that, for FeRe, ReFe antisites and Fe1–Re1, Fe1–Re4 interchanges cases, no obvious structural changes are observed due to the Fe3+ and Re5+ ions having similar radii of 0.78 Å and 0.72 Å,[46] respectively. However, from Figs. 1(e) and 1(f), we can see that, for VFe/VRe vacancy cases, the vanished attractions of the removed Fe/Re atom make its six nearest neighbor oxygen atoms move close to their nearest Re/Fe neighbors, so the corresponding Re–O/Fe–O bond lengths reduce to 1.881 Å/1.798 Å. While in perfect Sr2FeReO6, the optimized bond lengths are 1.937 Å/2.008 Å for Re–O/Fe–O bonds, as shown in Fig. 1(i). Figure 1(g) shows that the vanished repulsive forces of the removed oxygen atom make its eight nearest neighbor oxygen atoms move close to the VO vacancy site. Figure 1(h) shows that there are no obvious structural changes for the VSr vacancy case. As mentioned in our previous paper,[47] this is because the interactions between the Sr atom and its nearest neighbor atoms are very weak due to the completely filled Sr 4p and 5s subshells.

3.2. HM characters

In order to investigate the effects of the defects on the HM character of the double perovskite Sr2FeReO6, which are very important for its application in spintronic devices, we show in Fig. 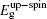2 the total density of states (DOS) of 4 f.u. Sr2FeReO6 containing eight different defects of (a) Fe antisite (FeRe), (b) Re antisite (ReFe), (c) Fe1–Re1 interchange (Fe1–Re1), (d) Fe1–Re4 interchange (Fe1–Re4), (e) Fe vacancy (VFe), (f) Re vacancy (VRe), (g) O vacancy (VO), or (h) Sr vacancy (VSr). We can see that, the HM characters are maintained for imperfect Sr2FeReO6 containing (a) FeRe antisite, (b) ReFe antisite, (d) Fe1–Re4 interchange, (e) VFe vacancy, (g) VO vacancy, or (h) VSr vacancy, because their down-spin channels (red lines) cross the Fermi level EF and the up-spin channels (black lines) open the band gaps of 0.614 eV, 0.769 eV, 0.757 eV, 1.371 eV, 1.527 eV, and 1.535 eV, respectively. On the contrary, the HM characters are lost for imperfect Sr2FeReO6 containing (c) Fe1–Re1 interchange and (f) VRe vacancy, since the total DOS of both down-spin (red lines) and up-spin (black lines) channels cross the Fermi level EF. The HM characters of the imperfect Sr2FeReO6 are lost for (c) Fe1–Re1 interchange at (0, 0, 0) and (0, 0, 0.5) sites but maintained for (d) Fe1–Re4 interchange at (0, 0, 0) and (0.5, 0.5, 0.5) sites, because the separation distance of 3.945 Å for Fe1–Re1 interchange is smaller than that of 6.833 Å for Fe1–Re4 interchange. So we conclude that the near Fe1–Re1 interchange and VRe vacancy defects should be avoided in order to preserve the HM characters of the Sr2FeReO6 and thus usage in spintronic devices.

Fig. 2. Total density of states (DOS) of imperfect Sr2FeReO6 of 4 f.u. containing (a) Fe antisite (FeRe), (b) Re antisite (ReFe), (c) Fe1–Re1 interchange (Fe1–Re1), (d) Fe1–Re4 interchange (Fe1–Re4), (e) Fe vacancy (VFe), (f) Re vacancy (VRe), (g) O vacancy (VO), or (h) Sr vacancy (VSr). The black and red lines represent up-spin and down-spin DOS, respectively, and the Fermi level EF is set at zero energy and indicated by the vertical blue lines.

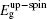
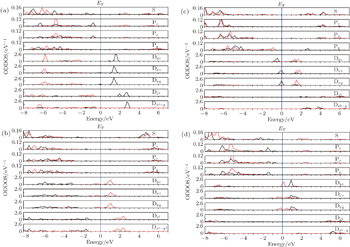
Now we turn to examine the disappearing reason of the HM character of the imperfect Sr2FeReO6 containing Fe1–Re1 interchange defect (see Figs. 1(c) and 2(c) for the structure and the total DOS). The detailed orbital-decomposed density of states (ODDOS) projected onto the concerned inequivalent Fe atoms at (0, 0, 0.5) FeRe antisite and (0.5, 0.5, 0) regular Fe site and Re atoms at (0, 0, 0) ReFe antisite and (0.5, 0.5, 0.5) regular Re site is shown in Fig. 3. It is clear that the total DOS of the down-spin channel (red line) crossing the Fermi level EF in Fig. 2(c) for the imperfect Sr2FeReO6 containing the Fe1–Re1 interchange defect resulted from the hybridizations of the t2g (dxy, dyz and dzx) states of the Fe and Re atoms at regular sites and antisites, while the occurrence of the up-spin state (marked with an arrow in Fig. 2(c)) in the band gap region of the perfect Sr2FeReO6, i.e., the disappearing reason of the HM character of the imperfect Sr2FeReO6 containing the Fe1–Re1 interchange defect, is attributed to the small bonding-antibonding splitting of the up-spin t2g (dxy, dyz and dzx) states of both antisite ReFe at (0, 0, 0) (especially) and near antisite FeRe at (0, 0, 0.5) with positive and negative magnetic moments, respectively. It should be pointed out that such a small bonding-antibonding splitting of the up-spin t2g (dxy, dyz and dzx) states also exists in the other imperfect Sr2FeReO6 with HM character, it is just because the split bonding state and the antibonding state of the up-spin t2g (dxy, dyz and dzx) orbitals do not cross the Fermi level EF and thus open the various up-spin band gaps (eV) as mentioned above.

Fig. 3. Orbital-decomposed density of states (ODDOS) projected onto the concerned inequivalent Fe atoms at (a) (0, 0, 0.5) FeRe antisite and (b) (0.5, 0.5, 0) regular Fe site and Re atoms at (c) (0, 0, 0) ReFe antisite and (d) (0.5, 0.5, 0.5) regular Re site for imperfect Sr2FeReO6 containing the Fe1–Re1 interchange defect (see Figs. 1(c) and 2(c) for the structure and the total DOS). The black and red lines represent up-spin and down-spin DOS, respectively, and the Fermi level EF is set at zero energy and indicated by the vertical blue lines.
3.3. Spin couplings and magnetic moments

In order to investigate the effects of the defects on the spin coupling and magnetic moments, we show the spin or difference charge densities (ρspin = ρup-spin − ρdown-spin) in Fig. 4 for imperfect 4 f.u. Sr2FeReO6 containing eight different defects of (a) Fe antisite (FeRe) at (0.5, 0.5, 0.5) site, (b) Re antisite (ReFe) at (0, 0.5, 0.5) site, (c) Fe1–Re1 interchange (Fe1–Re1) at (0, 0, 0) and (0, 0, 0.5) sites, (d) Fe1–Re4 interchange (Fe1–Re4) at (0, 0, 0) and (0.5, 0.5, 0.5) sites, (e) Fe vacancy (VFe) at (0, 0.5, 0.5) site, (f) Re vacancy (VRe) at (0.5, 0.5, 0.5) site, (g) O vacancy (VO) at (0.5, 0.5, 0.25) site, or (h) Sr vacancy (VSr) at (0.75, 0.75, 0.75) site. The spin charge density of the perfect 4 f.u. Sr2FeReO6 is also shown in Fig. 4(i) for comparison. The yellow (turquoise) isosurfaces represent the positive (negative) charge density of 0.005 e/Å3 and thus an up-spin (down-spin) moment. In the (100) cross sections, the colors blue, turquoise, and green represent the values of spin charge density in increasing order. We can see that, firstly, in cases of (a) FeRe antisite at (0.5, 0.5, 0.5) site, (b) ReFe antisite at (0, 0.5, 0.5) site, (c) Fe1–Re1 interchange at (0, 0, 0) and (0, 0, 0.5) sites, and (d) Fe1–Re4 interchange at (0, 0, 0) and (0.5, 0.5, 0.5) sites (each interchange contains one FeRe antisite pluses one ReFe antisite), the spin moments of the Fe (Re) cations situated on Re (Fe) antisites are coupled AFM with those of the Fe (Re) cations on the regular sites. We also make an FM configuration calculation for each case, i.e., all the Fe (Re) moments are positive (negative), but the total energies are 2.67 eV, 0.00 eV (in fact pushed to the AFM configuration), 0.36 eV, and 0.49 eV higher than the AFM ground states for the (a) FeRe antisite, (b) ReFe antisite, (c) Fe1–Re1 interchange, and (d) Fe1–Re4 interchange cases, respectively. Secondly, in cases of (e) VFe vacancy, (f) VRe vacancy, (g) VO vacancy, and (h) VSr vacancy, an FM coupling is observed within each cation sublattice, while the two cation sublattices are AFM coupled. This is similar to the perfect Sr2FeReO6 case shown in Fig. 4(i). Thirdly, as expected, each cation defect affects mainly its six nearest neighbor oxygen atoms. In cases of (a) FeRe antisite, (c) Fe1–Re1 interchange, (d) Fe1–Re4 interchange, (e) VFe vacancy, and (f) VRe vacancy, a partial negative spin moment (turquoise) presents on the six nearest neighbor oxygen atoms, while in the ReFe antisite case (b), no spin moments are observed on the six nearest neighbor oxygen atoms. Fourthly, the VO vacancy at (0.5, 0.5, 0.25) site causes the nearest neighbor Re4 cation at central (0.5, 0.5, 0.5) site having a much larger and expansive negative spin moment (turquoise) and its five survived nearest neighbor oxygen atoms having a partial negative spin moment (turquoise). Finally, no spin density distributions at eight Sr sites in cases (a)–(g) and no obvious influence on the magnetic moment distributions in case (h) both indicate that the contributions to the magnetic moment from the Sr atoms are neglectable.

Fig. 4. The spin charge density of imperfect Sr2FeReO6 of 4 f.u. containing (a) Fe antisite (FeRe) at (0.5, 0.5, 0.5) site, (b) Re antisite (ReFe) at (0, 0.5, 0.5) site, (c) Fe1–Re1 interchange (Fe1–Re1) at (0, 0, 0) and (0, 0, 0.5) sites, (d) Fe1–Re4 interchange (Fe1–Re4) at (0, 0, 0) and (0.5, 0.5, 0.5) sites, (e) Fe vacancy (VFe) at (0, 0.5, 0.5) site, (f) Re vacancy (VRe) at (0.5, 0.5, 0.5) site, (g) O vacancy (VO) at (0.5, 0.5, 0.25) site, or (h) Sr vacancy (VSr) at (0.75, 0.75, 0.75) site. The spin charge density of the perfect Sr2FeReO6 of 4 f.u. is also shown in panel (i) for comparison. The yellow (turquoise) isosurfaces represent positive (negative) charge density of 0.005 e/Å3 and thus an up-spin (down-spin) moment. In the (100) cross sections, the colors blue, turquoise, and green represent the values of spin charge density in increasing order.

The initial fractional coordinates (x, y, z) and local magnetic moments μ (μB) of the Fe and Re atoms on the regular site and antisites, the total magnetic moments μtot (μB/f.u.), the HM characters, and the up-spin band gaps 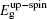(eV) of the imperfect 4 f.u. Sr2FeReO6 containing eight different defects are summarized in Table 1, together with the values of the perfect Sr2FeReO6 for comparison. It is clearly shown that, except for the VRe and VSr vacancy cases, the total magnetic moment μtot of the imperfect Sr2FeReO6 system with one of the other six different defects is smaller than that of the perfect one. So the smaller measured saturation magnetization of 2.7 μB/f.u. at 4.2 K in Sr2FeReO6[2] compared to the theoretical value of 3.0 μB/f.u. can be attributed to various defects. Furthermore, from Table 1, we can see that for the FeRe antisite case, the reduced saturation magnetization is resulted from the occurrence of antiparallel aligned magnetic moment −3.926 μB on FeRe antisite. For the ReFe antisite case, the reduced saturation magnetization is attributed to the fact that the supplied parallel aligned magnetic moment 1.561 μB by the ReFe antisite is smaller than the disappeared moment 3.696 μB of the substituted Fe. These two reducing magnetization mechanisms occur simultaneously in the Fe1–Re1 (Fe1–Re4) interchange cases, i.e. antiparallel aligned magnetic moments −3.929 μB (−3.915 μB) on FeRe antisites and supplied smaller parallel aligned magnetic moments 1.353 μB (1.400 μB) by ReFe antisites, leading to the much lower saturation magnetizations of 1.87 μB/f.u. (1.96 μB/f.u.). The vanishing of a regular site Fe atom and thus the vanishing of its parallel aligned magnetic moment (3.696 μB) is clearly responsible for the reduced saturation magnetization of the imperfect Sr2FeReO6 with VFe vacancy. Although removing a Re atom from its regular sublattice leads to decreasing parallel aligned magnetic moments on its three near Fe2, Fe3, and Fe4 neighbors, both the vanishing (decreasing) antiparallel aligned magnetic moment on itself (its three near Re1, Re2, and Re3 neighbors) and a slightly increasing parallel aligned magnetic moment on the Fe1 atom result in a larger saturation magnetization of 3.43 μB/f.u in imperfect Sr2FeReO6 with VRe vacancy. Although removing an oxygen atom causes slightly increasing parallel aligned magnetic moments on four Fe atoms on the regular sublattice, both the vanishing parallel aligned magnetic moment and especially the increasing antiparallel aligned magnetic moments on the four Re atoms on the regular sublattice still lead to the slightly smaller saturation magnetization of 2.64 μB/f.u. in the imperfect Sr2FeReO6 containing VO vacancy. Finally, the total magnetic moment μtot of the imperfect Sr2FeReO6 with VSr vacancy is larger than that of the perfect one. The reason is that not only the parallel aligned magnetic moment of about 3.90 μB for four Fe atoms is larger than that of 3.696 μB for four Fe atoms in perfect Sr2FeReO6, but also the antiparallel aligned magnetic moment of about −0.71 μB for four Re atoms is smaller than that of −0.857 μB for four Re atoms in perfect Sr2FeReO6, so the largest saturation magnetization of 3.50 μB/f.u. is found.

Table 1.

The initial fractional coordinates (x, y, z) and local magnetic moments μ (μB) of the Fe and Re atoms on the regular site and antisites, the total magnetic moments μtot (μB/f.u.), half-metallic characters, and up-spin band gaps (eV) of imperfect 4 f.u. Sr2FeReO6 containing eight different defects. The values corresponding to the perfect Sr2FeReO6 are also shown for comparison.

.
4. Conclusion

From the aspects of HM character and magnetization reduction, the structural, electronic, and magnetic properties of the imperfect Sr2FeReO6 containing eight different defects of FeRe or ReFe antisites, Fe1–Re1 or Fe1–Re4 interchanges, VFe, VRe, VO, or VSr vacancies have been studied by using the first-principles projector augmented wave (PAW) potential within the generalized gradient approximation as well as taking into account on-site the Coulomb repulsive interaction (GGA+U). The following results have been obtained.

Reference
1Kobayashi K IKimura TSawada HTerakura KTokura Y 1998 Nature 395 677
2Kobayashi K IKimura TTomioka YSawada HTerakura KTokura Y 1999 Phys. Rev. 59 11159
3Rao C N RRaveau B1998Colossal Magnetoresistance, Charge Ordering and Related Properties of Manganese OxidesSingaporeWorld Scientific Publishers
4Wolf S AAwschalom D DBuhrman R ADaughton J MMolnár S VRoukes M LChtchelkanova A YTreger D M 2001 Science 294 1488
5Tomioka YOkuda TOkimoto YKumai RKobayashi K ITokura Y 2000 Phys. Rev. 61 422
6Chmaissem OKruk RDabrowski BBrown D EXiong XKolesnik SJorgensen J DKimball C W 2000 Phys. Rev. 62 14197
7Navarro JFrontera CBalcells LMartìnez BFontcuberta J 2001 Phys. Rev. 64 092411
8Moreno M SGayone J EAbbate MCaneiro ANiebieskikwiat DSánchez R DSiervo A deLanders RZampieri G 2002 Physica 320 43
9Jung AKsenofontov VReiman STherese H AKolb UFelser CTremel W 2006 Phys. Rev. 73 144414
10Jung ABonn IKsenofontov VPanthöfer MReiman SFelser CTremel W 2007 Phys. Rev. 75 184409
11Ohno KKato HNishioka TMatsumura M 2007 J. Magn. Magn. Mater. 310 e666
12Hu Y CGe J JJi QJiang Z SWu X SCheng G F 2010 Mater. Chem. Phys. 124 274
13Pan Y WZhu P WWang X 2015 Chin. Phys. 24 017503
14Sarma D DMahadevan PSaha-Dasgupta TRay SKumar A 2000 Phys. Rev. Lett. 85 2549
15Moritomo YXu ShAkimoto TMachida AHamada NOhoyama KNishibori ETakata MSakata M 2000 Phys. Rev. 62 14224
16Fang ZTerakura KKanamori J 2001 Phys. Rev. 63 180407
17Wu H 2001 Phys. Rev. 64 125126
18Solovyev I V 2002 Phys. Rev. 65 144446
19Jeng H TGuo G Y 2003 Phys. Rev. 67 094438
20Saha-Dasgupta TSarma D D 2001 Phys. Rev. 64 064408
21Ogale A SOgale S BRamesh RVenkatesan T 1999 Appl. Phys. Lett. 75 537
22Ray SKumar ASarma D DCimino RTurchini SZennaro SZema N 2001 Phys. Rev. Lett. 87 097204
23Munoz-García A BPavone MCarter E A 2011 Chem. Mater. 23 4525
24Kircheisen RTöpfer J 2012 J. Solid State Chem. 185 76
25Meneghini CRay SLiscio FBardelli FMobilio SSarma D D 2009 Phys. Rev. Lett. 103 046403
26Balcells LNavarro JBibes MRoig AMartinez BFontcuberta J 2001 Appl. Phys. Lett. 78 781
27Zhu X FLi Q FChen L F 2007 Solid State Commun. 144 230
28Stoeffler DColis S 2005 J. Magn. Magn. Mater. 290�?91 400
29Stoeffler DColis S 2006 Mater. Sci. Eng. 126 133
30Stoeffler DEtz C 2006 J. Phys.: Condens. Matter 18 11291
31Frontera CFontcuberta J 2004 Phys. Rev. 69 014406
32Retuerto MMartínez-Lope M JGarcía-Hernández MAlonso J A 2009 Mater. Res. Bull. 44 1261
33Blanco J JInsausti MLezama LChapman J PGil de Muro IRojo T 2004 J. Solid State Chem. 177 2749
34Blasco JRodríguez-Velamazán J ARitter CSesé JStankiewicz JHerrero-Martín J 2009 Solid State Sci. 11 1535
35Li Q FZhu X FChen L F 2008 Phys. Lett. 372 2911
36Li Q FWang LSu J L 2011 Mod. Phys. Lett. 25 2259
37Wang JZhang J MWang S FXu K W 2013 J. Magn. Magn. Mater. 329 30
38Kresse GHafner J 1993 Phys. Rev. 47 558
39Kresse GHafner J 1994 Phys. Rev. 49 14251
40Kresse GFurthmüller J 1996 Comput. Mater. Sci. 6 15
41Kresse GFurthmüller J 1996 Phys. Rev. 54 11169
42Kresse GJoubert D 1999 Phys. Rev. 59 1758
43Perdew J PBurke KErnzerhof M 1996 Phys. Rev. Lett. 77 3865
44Saitoh TNakatake MKakizaki ANakajima HMorimoto OXu ShMoritomo YHamada NAiura Y 2002 Phys. Rev. 66 035112
45Monkhorst H JPack J D 1976 Phys. Rev. 13 5188
46Shannon R D 1976 Acta Cryst. 32 751
47Zhang YJi V 2012 Physica 407 912