Cite this Article
Shi Zhe, Yang Yang, Gan Lin, Li Zhi-Yuan. Broadband tunability of surface plasmon resonance in graphene-coating silica nanoparticles. Chinese Physics B, 2016, 25(5): 057803  
Permissions
Broadband tunability of surface plasmon resonance in graphene-coating silica nanoparticles
Shi Zhe1, †, , Yang Yang1, 2, †, , Gan Lin1, Li Zhi-Yuan‡,
Laboratory of Optical Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
Key Laboratory of Micro-nano Measurement-Manipulation and Physics (Ministry of Education), Department of Physics, Beihang University, Beijing 100191, China

 

† These authors contribute equally to this work.

‡ Corresponding author. E-mail:lizy@aphy.iphy.ac.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11204365 and 11434017) and the National Basic Research Program of China (Grant No. 2013CB632704).

Abstract
Abstract

Graphene decorated nanomaterials and nanostructures can potentially be used in military and medical science applications. In this article, we study the optical properties of a graphene wrapping silica core–shell spherical nanoparticle under illumination of external light by using the Mie theory. We find that the nanoparticle can exhibit surface plasmon resonance (SPR) that can be broadly tuned from mid infrared to near infrared via simply changing the geometric parameters. A simplified equivalent dielectric permittivity model is developed to better understand the physics of SPR, and the calculation results agree well qualitatively with the rigorous Mie theory. Both calculations suggest that a small radius of graphene wrapping nanoparticle with high Fermi level could move the SPR wavelength of graphene into the near infrared regime.

PACS: 78.67.Wj;78.67.Bf;73.20.Mf;
Keyword:graphene;core–shell nanoparticle;surface plasmon resonance;
1. Introduction

Graphene is a two-dimensional (2D) material composed of one layer of carbon atoms arrayed in a honeycomb lattice. It has an unusual linear dispersion band structure and ultra-high electron mobility at room temperature.[1,2] Due to its low carrier quantity, the Fermi level of graphene can be easily adjusted by electrostatic gate or chemical doping method.[1,3] With these significant novel properties, graphene shows great potential in making next generation high frequency field effect transistors (FET) to 100 GHz[4,5] to overpass the limit of silicon transistors.

Beyond the interests in electronics, much research interests in photonic and optoelectronic properties of graphene[6] have been aroused recently. Graphene can be integrated with nanophotonic structures, such as waveguide,[7] cavity,[8] fiber,[9] and even solar cell[10] to make the devices have more functionalities, such as faster modulation efficiency and higher energy exchange efficiency. Usually the interaction between graphene and light is fairly weak, e.g., it is well known that only 2.3% of the incident light in visible and near-infrared spectrum range is absorbed by graphene.[11] In order to enhance the interaction, three methods are usually adopted. The first one is to introduce an electromagnetic field confinement mechanism by placing plasmonic structures[12–14] on graphene or adhering graphene on resonant cavities.[15–17] The second one is to make the graphene interact with electromagnetic field for a longer distance, e.g., by integrating graphene with waveguides[7] and fibers.[9] The third one is to excite the intrinsic plasmon resonance in graphene, e.g., by fabricating graphene ribbons[18] or placing graphene on gratings.[19] However, all of those schemes are based on a planar device structure, where graphene is placed on a 2D optical structure and usually a plasmonic resonance wavelength at mid-infrared wavelength with limited tunability is observed, probably due to the 2D properties of graphene and optical structures.

Suppose graphene is integrated with a zero-dimensional (0D) optical nanostructure, such as covering graphene on the surface of a nanoparticle, what will happen? Some pioneering works have been done in these fields. For instance, wrapping oxidized graphene on a hollow SnO2 ball can make high-performance anode materials for lithium ion batteries,[20] and a hetero-structure of graphene covered silicon carbide (SiC) nanoparticle, directly grown by decomposing SiC, shows great potential in photocatalytic and hydrogen production.[21,22] The novel properties of these graphene decorated nanoparticles indicate that the platform of an integrated graphene-nanoparticle composite could bring new phenomena and functionalities that are absent in pure graphene.

To further explore the novel optical phenomena and properties in these graphene hybrid nanostructures, we propose a model structure of integrating graphene on the curved surface of a nanoparticle to enhance the interaction of graphene with light through the curved graphene surface. Because of the curved surface, local surface plasmon resonance (SPR) can be excited in graphene wrapped on the nanoparticle surface, and the SPR wavelength can be modulated in a broad range from mid-infrared to near infrared wavelength, which is useful for military and medical science applications.

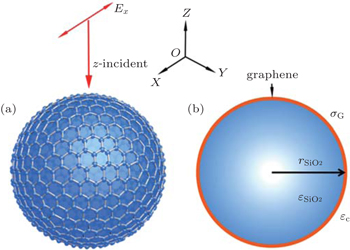
As a principle model, we study a graphene coating silica spherical nanoparticle and theoretically calculate the SPR wavelength as functions of graphene Fermi levels and the geometric of the silica nanoparticle. In our graphene coating nanoparticle model, graphene is anisotropic. To calculate SPR preciously, Mie theory[23] should be used, which is a little bit complicated for this composite nanoparticle. Notice that the size of nanoparticle (< 100 nm) is much smaller than the wavelength of light (several micrometers), we can use a simple approach called the equivalent dielectric permittivity theory to estimate the optical response characteristic of this composite nanoparticle. The equivalent dielectric permittivity theory is much simpler and easier to use than Mie theory to obtain the resonance spectrum. The calculation results from the two theoretical models will be compared and analyzed. It turns out that the equivalent dielectric permittivity theory could conveniently predict the resonance spectrum of the hybrid graphene–nanoparticle structure with a sufficiently good precision, but without a complex calculation as used in Mie theory. Besides, the 0D hybrid structure of graphene and silica nanoparticle could act as a new platform for enhancing the optical response for near infrared light.

2. Physical model

In this work, a small spherical core–shell nanoparticle with a core component of silica and a shell of a monolayer of graphene covering the outer surface of the silica nanoparticle is studied. A plane wave light propagating along the z-axis direction with the linear polarized electric field in the x-axis direction is used to excite the SPR of the nanoparticle. The geometry of the core–shell nanostructure is schematically shown in Fig. 1, where the nanoparticles are placed in the medium with permittivity of εc, the silica core has a radius of rSiO2, and the thickness of wrapped graphene shell is tG. The thickness of monolayer graphene is usually adopted as 0.34 nm. Here, we set it as 1 nm in all of our calculations and simulations similar to the method used many others.[12,13] In addition, the radius of silica core and Fermi level of graphene are taken as adjustable parameters to examine their influence on SPR, which are varied from 10 nm to 100 nm in a step of 10 nm, and from 0.3 eV to 1.0 eV in a step of 0.1 eV, respectively. The dielectric constant of silica εSiO2 is taken as 1.45 according to Palik.[24] The dielectric constant of graphene can be calculated from its relation with the optical conductivity σG(ω),[12] which can be expressed as ε∥(ω) = ε⊥ + iσG(ω)/ω ε0tG. Here ε∥ is the dielectric constant of graphene in plane, ε⊥ is the dielectric constant of graphene out of plane (it is taken as 2.5, the same as graphite), ω and ε0 are the frequency of excitation light and the vacuum dielectric constant, respectively. The optical conductivity of graphene is calculated with the random-phase approximation (RPA) under condition of the local limit based on the Kubo formalism. It contains both of the interband σinter and intraband σintra conductivity contribution terms[25] expressed as

Fig. 1. Schematic of a 0D core–shell structure with graphene wrapping on silica nanoparticle. (a) The light blue ball presents the silica core with a radius of rSiO2, and its surface is covered with a monolayer of graphene in thickness of tG. A plane wave propagating along the z-axis with the electric field polarized along the x axis is used to excite SPR in graphene wrapping silica nanoparticle. (b) The cross-section schematic of the core–shell structure of the graphene wrapping nanoparticle.

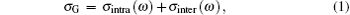
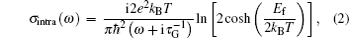
Here, e is the elemental electron charge, kB is the Boltzmann constant, ħ is the Planck constant, T is the temperature (here, a room temperature of 300 K is used), Ef is the Fermi level of graphene, and τG is the carrier relaxation time in graphene. The graphene permittivity ε∥ can be changed by variation of the Fermi level of graphene. Here, we set the graphene mobility as 10000 cm2/V·s, which is commonly used in other calculations.[12] Thus, we can deduce the value of ε∥ at different Fermi levels of graphene from the above relation.

When the SPR of the core–shell nanoparticle is excited, its extinction spectrum and resonance peak position can be calculated based on our theoretical models. In our calculations, the two theoretical models mentioned above are adopted to find the SPR peak of the graphene-covering silica nanoparticles. One is calculated by the equivalent dielectric permittivity method applied to the core–shell nanoparticle and the other is calculated by precise Mie theory. These two models give similar results and their pros and cons are also analyzed and discussed.

3. Theoretical method
3.1. Mie theory

Mie theory is a precise calculation method widely used in describing the scattering of an electromagnetic plane wave by a homogeneous sphere or stratified spheres.[23] It can handle any size of the scattering particles, whether comparable to, much smaller than or much larger than the wavelength of the light. Using the Mie theory, we can precisely calculate the extinction spectrum of the graphene wrapped core–shell nanoparticle[26,27] under illumination of an incident plane wave, as illustrated in Fig. 1.

In this model, the surface current J is flowing in the graphene shell coated on the spherical dielectric particle. The boundary conditions at the interface between graphene and silica surface are considered, where the component of the total tangential electric field E on the interface is continuous and the component of the total tangential magnetic field H on the interface is discontinuous, which is proportional to the surface current density. The boundary conditions can be expressed as[28]

where er is the associated unit vector normal to the interface, Ei (Hi), Es (Hs), and Ev(Hv) respectively represent the incident, scattering, and internal electric (magnetic) fields of the graphene wrapped core–shell nanoparticle. The surface current J is proportional to the surface electric field E∥ and the proportional coefficient is the optical conductivity of graphene expressed as J = σ(ω)E∥.

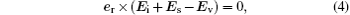
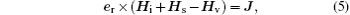
The time-harmonic electromagnetic field E(r,ω) in a medium with a dielectric constant ε(ω) must satisfy the Helmholtz wave equation

where k0 is a wave vector in free space. According to the Mie theory, in a system with spherical symmetry, the incident electromagnetic field can be expressed in a spherical coordinate expression by vector spherical functions of and as

where the vector spherical functions can be express as

Here, is the associated first kind Legendre function with degree n and order m. is selected from four of the spherical Bessel functions: j = 1, 2, 3, and 4 denote the first kind of Bessel function jn, the second kind of Bessel function yn and the Hankel functions of and , respectively. ir, iθ, and iϕ are the unit vector along the radial, polar, and azimuthal coordinate directions, respectively. The scattering field Es (r) can be expressed as

The internal field Ev (r) has the similar form of expression. Enforcing the boundary conditions at the core–cell particle surface for the incident, scattering, and inner wave amplitudes, the multipole expansion coefficients of the scattering electromagnetic field by the graphene coated core–shell nanoparticle can be readily derived and calculated.

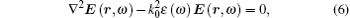
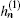
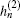
The normalized extinction cross section can be expressed as

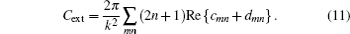
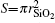
Here, k is the wave vector of incident wave. Suppose is the geometric cross-section for a spherical particle, the optical extinction coefficient Qext can be expressed as Qext = Cext/S.

3.2. Equivalent dielectric permittivity model

Due to the low carrier density in graphene, the SPR peak of intrinsic graphene nanostructures are located in mid-infrared wavelength (∼ 7–8 μm). As the size of the nanoparticle considered in our structural model is very small compared to the resonance wavelength, i.e., a 50-nm nanoparticle radius is only one percent of the resonance wavelength. Thus, we can treat the core–shell graphene wrapped nanoparticle as an isotropic homogenous particle with an equivalent homogenous dielectric permittivity without considering graphene as an anisotropic dielectric material and distinguishing the material difference between the core and shell.

In using the equivalent dielectric permittivity approximation, we can treat the anisotropic dielectric permittivity of graphene as an equivalent isotropic dielectric permittivity material by setting its equivalent dielectric permittivity as

because the scattering of light can be equivalently contributed from both the in-plane and out-of plane components instead of only a 2D in-plane contribution, when graphene bends on the curved surface of the silica nanoparticle. Thus each of the field components in the three definite directions (x, y, z) contributes one third to the dielectric permittivity εeq−G. Furthermore, we equivalently approximate the core–shell graphene wrapping nanoparticles as a uniform dielectric permittivity material by weighting their contributions according to their volume fractions, expressed as

where εnp is the equivalent dielectric permittivity of the core–shell graphene wrapping nanoparticle, f is the volume fraction of graphene. Because the size of the nanoparticle is very small compared with the SPR wavelength, the extremely thin thickness of the graphene shell in the core–shell structure can be hardly detected by the incident light and the simple uniform particle approximation can be valid for simulation. Therefore it is reasonable to treat the core–shell graphene wrapping nanoparticle as an isotropic uniform nanoparticle with dielectric permittivity of εnp in the equivalent dielectric permittivity method.

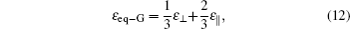
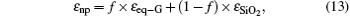
Then the scattering, absorption, and extinction cross sections, which are Csca, Cabs, and Cext, respectively, of the core–shell graphene wrapping nanoparticle, with an equivalent dielectric permittivity of εnp, can be calculated via the following relation:[26]

Here, k is the wave vector of incident wave, R = rSiO2 is the radius of the nanoparticle, and εc is the permittivity of the surrounding environment. Here, we suppose the nanoparticle is embedded in air with εc = 1. By using this equivalent permittivity approximation, the small spherical core–shell graphene–silica nanoparticle is treated as an isotropic homogenous particle and its extinction spectrum can be calculated easily and conveniently.

4. Result and discussion

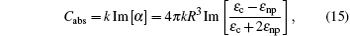
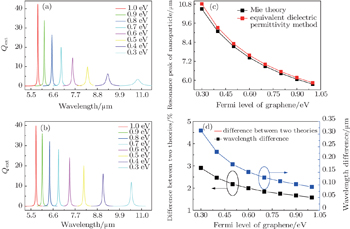
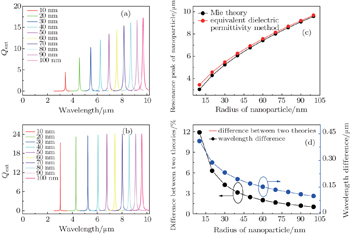
According to the two models described above, the SPR extinction spectra of the core–shell graphene wrapping core–shell nanoparticle can be calculated with different radii of the nanoparticles and different Fermi levels of graphene covering on the surface. The extinction spectra of the nanoparticle calculated based on the equivalent dielectric permittivity method and Mie theory are shown in Fig. 2. Their similarities and differences are compared and analyzed in details.

4.1. Effects of graphene Fermi levels on extinction spectra

As is well known, there are many methods to modulate the Fermi level of graphene on a nanoparticle, such as putting the nanoparticle in an electrical field induced by applying an electrostatic gating. On the other hand, a uniform modulation of the Fermi level of graphene can be obtained through chemically doping graphene with boron or nitrogen element.[29]

As graphene is coating on a silica nanoparticle surface, the core–shell structure is constructed. The calculated extinction spectra at different Fermi levels of graphene varying from 1.0 eV to 0.3 eV in a step of 0.1 eV are shown in Fig. 2, where the radius of the core–shell structure is fixed at 60 nm. The extinction spectrum changes with Fermi levels of graphene in both theoretical models. The results calculated from the equivalent dielectric permittivity model and Mie theory are shown in Figs. 2(a) and 2(b), respectively. A monotonical red shift of the resonance peak and decrease in the Qext intensity are observed in both calculations as the Fermi level of graphene moves towards its Dirac point. The resonance peaks change from 5.8 to 10.5 μm as the Fermi level of graphene decreases from 1.0 to 0.3 eV. The resonant peak positions calculated by the two models at the same Fermi level are slightly different as shown in Fig. 2(c), where the red symbols indicate the resonant peaks calculated by the equivalent dielectric permittivity model and the black symbols are the results calculated by Mie theory. Under the same carrier concentration the equivalent dielectric permittivity method gives slightly longer resonant peak wavelength than the Mie theory.

The difference of the resonant wavelengths at the same Fermi level calculated by the two models are shown in Fig. 2(d) as expressed with the filled blue square symbols, together with the relative ratio of the resonant wavelength difference calculated by Mie theory as expressed with the black square symbols. It is found that both of the difference and its relative ratio become smaller as the Fermi level of graphene gets larger. In the whole range of graphene Feimi levels considered here, a less than 5% relative difference is always observed between the two models and the difference gets smaller as the Fermi level gets larger. This indicates that the approximate equivalent dielectric permittivity model is a simple and convenient method to estimate the extinction spectrum of the core–shell graphene-silica nanoparticle with a reasonably good precision, and the larger the graphene Fermi level, the higher the precision of the approximate model.

Fig. 2. Extinction spectra of graphene wrapping core–shell nanoparticle with different Fermi levels of graphene. Extinction spectra calculated by (a) the equivalent dielectric permittivity method and (b) the Mie theory with the Fermi level of graphene wrapping silica nanoparticle change from 1.0 eV to 0.3 eV, while keeping the radius of the graphene wrapping nanoparticle fixed at 60 nm. (c) The changes of resonance peak with Fermi levels of graphene calculated by the two theories. (d) Relative resonant peak difference between the two theories for different Fermi levels of graphene.
4.2. Effects of the core–shell nanoparticle size on the extinction spectra

Besides the Fermi level induced change on the extinction spectrum, the effect of the nanoparticle radius on the extinction spectrum is studied further. In our calculations, we change the core–shell graphene wrapping nanoparticle radius from 10 to 100 nm in a step of 10 nm while keeping the Fermi level of graphene fixed at 0.6 eV. The extinction spectrum with different radii of nanoparticle calculated by the equivalent dielectric permittivity model and Mie theory are shown in Figs. 3(a) and 3(b), respectively. A red shift of the resonance peak accompanied with an enhanced intensity is observed obviously as the radius of nanoparticle becomes larger. The resonance peak changes from 3 to 9.5 μm as the radius of nanoparticle changes from 10 to 100 nm, as shown in Fig. 3(c), where the red and black symbols represent the results calculated by the equivalent dielectric permittivity model and Mie theory, respectively. The equivalent dielectric permittivity model gives a longer SPR wavelength than the Mie theory. The differences at different nanoparticle radii are shown in Fig. 3(d) expressed by the blue circle. The relative ratio of the wavelength difference is less than 12% in the considered range of the radius, and it becomes smaller as the particle radius get larger. A relatively large ratio of the difference (∼ 12%) in the 10-nm nanoparticles is due to the smaller resonant wavelengths. Despite this, the overall precision of the approximate equivalent dielectric permittivity model in predicting the SPR properties of the core–shell graphene–silica nanoparticle is satisfactory.

Fig. 3. Extinction spectra of graphene wrapping core–shell nanoparticle with different radii. Extinction spectra calculated by (a) the equivalent dielectric permittivity method and (b) the Mie theory with the radius of graphene wrapping silica nanoparticle changing from 10 to 100 nm, while keeping the graphene Fermi level fixed at 0.6 eV. (c) The change of resonance peak with different radii of nanoparticle calculated by the two theories. (d) The relative resonant peak difference between the two theories at different radii of nanoparticle.
4.3. Tuning core–shell nanoparticle SPR wavelength to near infrared

A more important thing to notice from the above systematic calculations is that one can use simple geometric configuration factor of nanoparticle to tune the SPR wavelength of graphene material in a very broad wavelength range. Remarkably one can combine an appropriate value of both the nanoparticle size (from the structural aspect) and graphene doping level (from the material aspect) to realize SPR of graphene in the near infrared wavelength. For instance, a graphene wrapping nanoparticle as small as 10 nm together with a high doping level (with the corresponding Fermi level of 1.0 eV) could possibly push the SPR wavelength to near infrared (∼ 2 μm), according to the calculation as shown in Fig. 4. In contrast, if only the material aspect of graphene is considered, then it can never happen that the graphene plasmon resonance is engineered to move to near infrared wavelength. It can be expected that if other more complicated geometry of nanoparticles is adopted to allow for high-order plasmonic modes to be excited, which has been well established in metal nanoparticles,[30–32] the SPR wavelength of graphene can further blue shift to the telecommunication wavelength (∼ 1.55 μm) or even the visible wavelength regime. As the graphene–silica hybrid nanoparticle is similar to the metal-shell dielectric-core composite core–shell nanoparticle widely studied in plasmonics,[30–32] the fine tunability of SPR wavelength within a broad range spectral range becomes a natural thing.

Fig. 4. Extinction spectrum of graphene wrapping core–shell nanoparticle with a dope level of 1.0 eV Fermi energy and radius of 10 nm. The resonance peak of graphene coating core–shell nanoparticle can move to near infrared wavelength.
5. Conclusion

In summary, we have proposed a graphene wrapping dielectric nanoparticle to engineer the plasmon resonance of graphene material via geometric resonance effect. The extinction spectra of the core–shell hybrid nanoparticle are calculated by using the rigorous Mie theory and a simple equivalent dielectric permittivity approximate model. The similarity and difference of the results calculated from the two theories are analyzed and discussed. It is found that the approximate model can yield the SPR wavelength of hybrid nanoparticles with a reasonably good precision compared with the rigorous Mie theory. Together with its simplicity, this effective medium approach could be very useful for estimating the optical properties of graphene hybrid nanoparticles and for engineering the SPR wavelength of graphene material.

Our calculation results show that the hybrid nanoparticle enables fine and sensitive tuning of the SPR wavelength of graphene material in a broad range from far infrared, to mid infrared, and even to near infrared regime simply by adjusting the radius of the nanoparticle and the doping level of graphene. When the structural and material aspect of the hybrid nanoparticle are closely explored and incorporated, a graphene wrapping nanoparticle with a small radius (around 10 nm) together with a high Fermi level (around 1.0 eV) will trigger a plasmonic resonance into near infrared. The broad spectral range tunability of plasmon resonance of graphene through this simple hybrid nanoparticle scheme could be potentially useful for military and medical science applications.

Reference
1Geim A KNovoselov K S 2007 Nat. Mater. 6 183
2Neto A H CGuinea FPeres N M RNovoselov K SGeim A K 2009 Rev. Mod. Phys. 81 109
3Liu HLiu YZhu D 2011 J. Mater. Chem. 21 3335
4Lin Y MDimitrakopoulos CJenkins K AFarmer D BChiu H YGrill AAvouris P 2010 Science 327 662
5Liao LLin Y CBao M QCheng RBai J WLiu YQu Y QWang K LHuang YDuan X F 2010 Nature 467 305
6Bonaccorso FSun ZHasan TFerrari A C 2010 Nat. Photon. 4 611
7Liu MYin X BUlin-Avila EGeng B SZentgraf TJu LFeng WZhang X 2011 Nature 474 64
8Phare C TLee Y H DCardenas JLipson M 2015 Nat. Photon. 9 511
9Li WChen B GMeng CFang WXiao YLi X YHu Z FXu Y XTong L MWang H QLiu W TBao J MShen Y R 2014 Nano Lett. 14 955
10Wang XZhi LMüllen K 2008 Nano Lett. 8 323
11Nair R RBlake PGrigorenko A NNovoselov K SBooth T JStauber TPeres N M RGeim A K 2008 Science 320 1308
12Yao YKats M AGenevet PYu N FSong YKong JCapasso F 2013 Nano Lett. 13 1257
13Emani N KChung T FNi X JKildishev A VChen Y PBoltasseva A 2012 Nano Lett. 12 5202
14Fang Z YLiu ZWang YAjayan P MNordlander PHalas N J 2012 Nano Lett. 12 3808
15Gu TPetrone NMcMillan J FZande A V DTu MLo G QKwong D LHone JWong C W 2012 Nat. Photon. 6 554
16Majumdar AKim JVuckovic JWang F 2013 Nano Lett. 13 515
17Shi ZGan LXiao T HGuo H LLi Z Y 2015 ACS Photonics 2 1513
18Ju LGeng B SHorng JGirit CMartin MHao ZBechtel H ALiang X GZettl AShen Y RWang F 2011 Nat. Nano. 6 630
19Gao WShu JQiu CXu Q 2012 ACS Nano 6 7806
20Yang HHou ZZhou NHe BCao JKuang Y 2014 Ceram. Int. 40 13903
21Zhu K XGuo L WLin J JHao W CShang JJia Y PChen L LJin S FWang W JChen X L 2012 Appl. Phys. Lett. 100 023113
22Lu WWang DGuo L WJia Y PYe M PHuang JLi Z LPeng YYuan W XChen X L 2015 Adv. Mater. 27 7986
23Bohren C FHuffman D R2008Absorption and Scattering of Light by Small ParticlesJohn Wiley & Sons8210082–100
24Palik E D1998Handbook of Optical Constants of Solids (Book 3)Academic Press
25Falkovsky L APershoguba S S 2007 Phys. Rev. 76 153410
26Christensen TJauho A PWubs MMortensen N A 2015 Phys. Rev. 91 125414
27Yang BWu TYang YZhang X 2015 J. Opt. 17 035002
28Jackson J D1998Classical Electrodynamics3rd ednNew YorkWiley157159157–9
29Panchakarla L SSubrahmanyam K SSaha S KGovindaraj AKrishnamurthy H RWaghmare U VRao C N R 2009 Adv. Mater. 21 4726
30Li J FLi Z Y 2014 Chin. Phys. 23 047305
31Zhou FLi Z YLiu YXia Y N 2008 J. Phys. Chem. 112 20233
32Hu MPetrova HSekkinen A RChen J YMcLellan J MLi Z YMarquez MLi X DXia Y NHartland G V 2006 J. Phys. Chem. 110 19923